スポンサーリンク
第二種電気工事士学科試験の4択クイズ 分岐回路の開閉器および過電流遮断器の施設
※ページ内にPR・広告が含まれる場合があります。
第二種電気工事士学科試験で出題されている分岐回路の開閉器および過電流遮断器の施設について4択クイズ(一問一答)にしてみました。(このページでは、2択の問題もありますが…。)
選択肢の中から答えを選ぶと解説も表示されるようになっているので、ちょっとした練習問題としても使えるんじゃないかなと思います。
スマホでもできるので(たぶん)、休憩時間やちょっと時間があいたときなど、スキマ時間にポチポチやってみるのもいいかもです。
計算が必要な問題については、選択肢の中に計算式と計算結果も書いています。紙と鉛筆を準備してわざわざ手計算をしなくてもいいようになっていますので、外出先などでもポチポチさくさく進められると思います。
また、このページの4択クイズをやってみて、
ぜんぜん分かんない!
というときは、こちらの分岐回路の開閉器および過電流遮断器の施設(電技解釈第149条)のページを一度読んでみてからやってみてください。
一度読んでからなら、そこそこいけると思います。
スポンサーリンク
分岐回路の開閉器および過電流遮断器の施設の4択クイズ
問題1
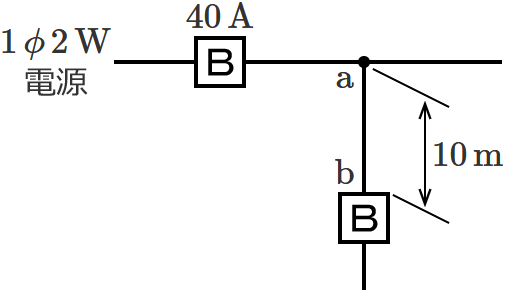
図のように定格電流 $\boldsymbol{40\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{10\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{22}$です。
問題の分岐回路の過電流遮断器は、分岐点から $10\,\mathrm{m}$ の位置に施設されます。$8\,\mathrm{m}$ を超える位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $55\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.55}\times I_B$ $=0.55\times 40$ $=22$ $\therefore\color{#f33}{22}\,\mathrm{A}$ になります。
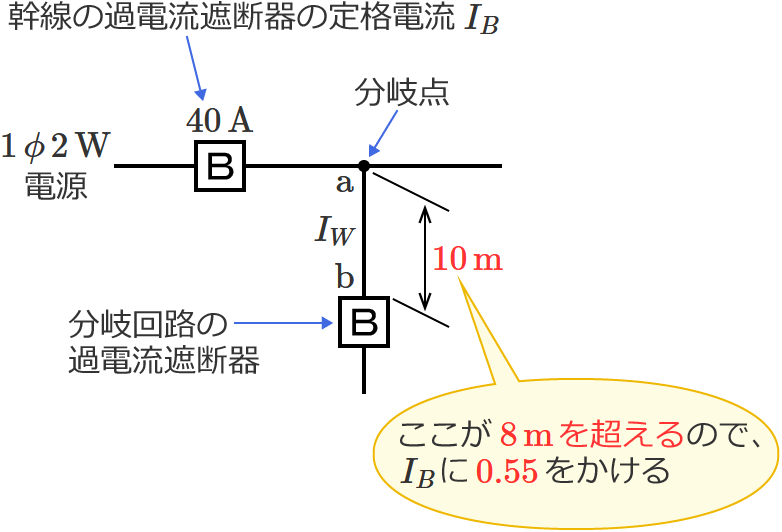
この問題1のような電線の許容電流の最小値を求める問題では、分岐点から分岐回路の過電流遮断器までの距離(図の $\mathrm{a}$-$\mathrm{b}$ 間の距離)がポイントになります。
- 分岐点から分岐回路の過電流遮断器までの距離が $8\,\mathrm{m}$ を超える場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $55\,\%$ 以上にしなければならない(なので、$8\,\mathrm{m}$ を超える場合は、$I_B$ に $0.55$ をかけて電線の許容電流の最小値を求める)
- 分岐点から分岐回路の過電流遮断器までの距離が $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上にしなければならない(なので、$3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の場合は、$I_B$ に $0.35$ をかけて電線の許容電流の最小値を求める)
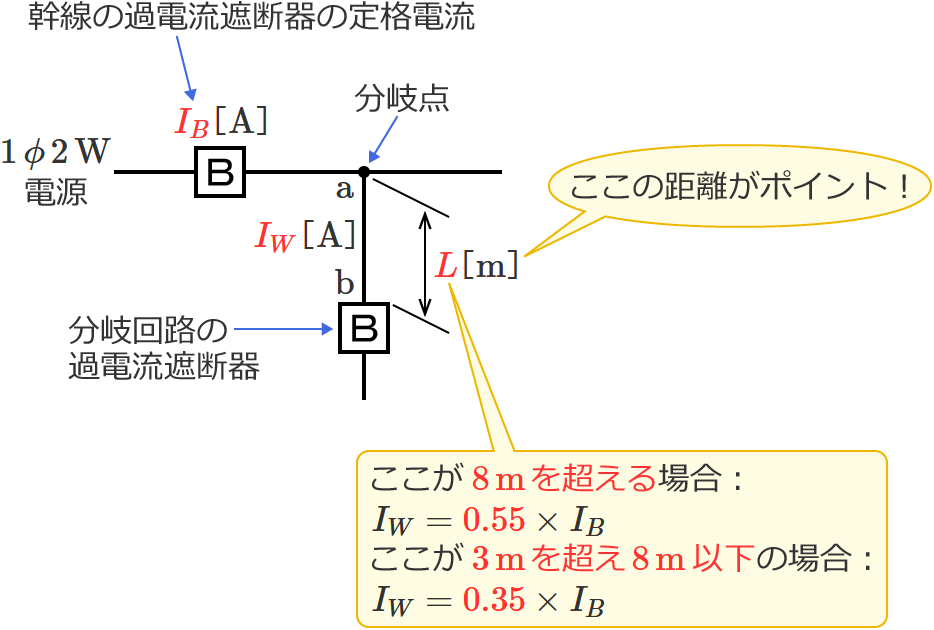
電線の許容電流の最小値を求める問題では、分岐点から分岐回路の過電流遮断器までの距離に着目しましょう!
問題2
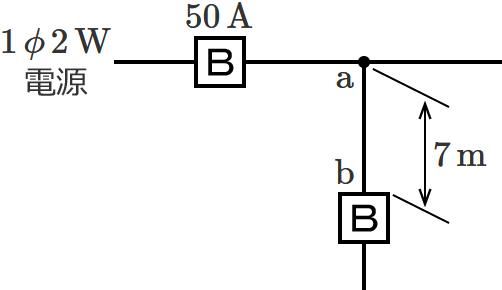
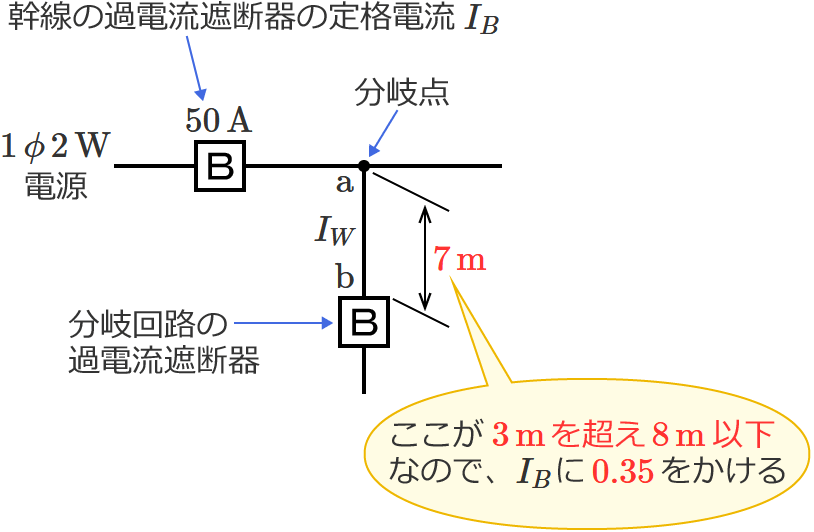
図のように定格電流 $\boldsymbol{50\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{7\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{17.5}$です。
問題の分岐回路の過電流遮断器は、分岐点から $7\,\mathrm{m}$ の位置に施設されます。$3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.35}\times I_B$ $=0.35\times 50$ $=17.5$ $\therefore\color{#f33}{17.5}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
問題3
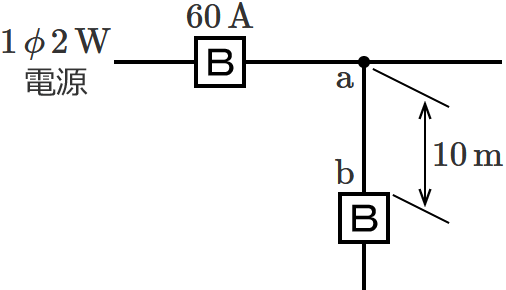
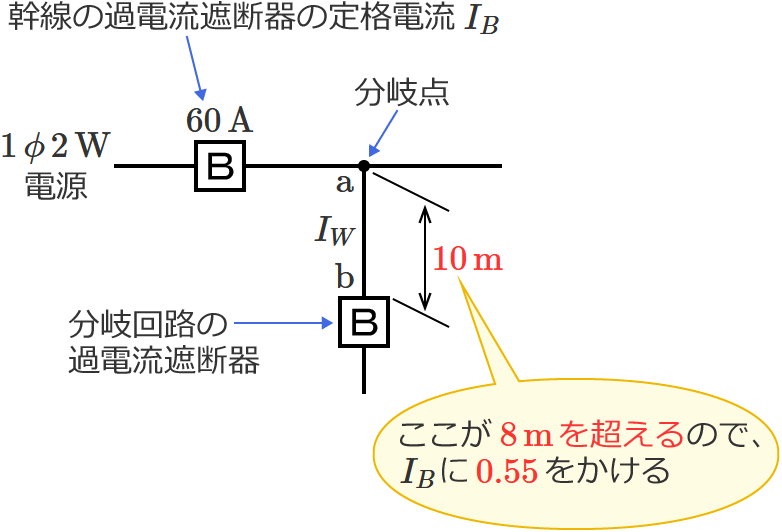
図のように定格電流 $\boldsymbol{60\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{10\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{33}$です。
問題の分岐回路の過電流遮断器は、分岐点から $10\,\mathrm{m}$ の位置に施設されます。$8\,\mathrm{m}$ を超える位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $55\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.55}\times I_B$ $=0.55\times 60$ $=33$ $\therefore\color{#f33}{33}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
問題4
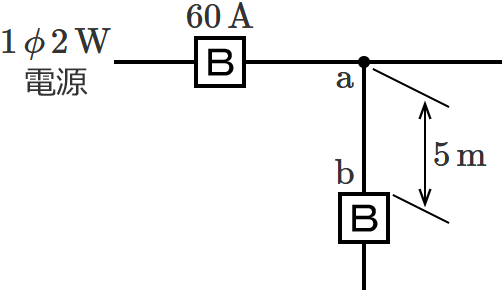
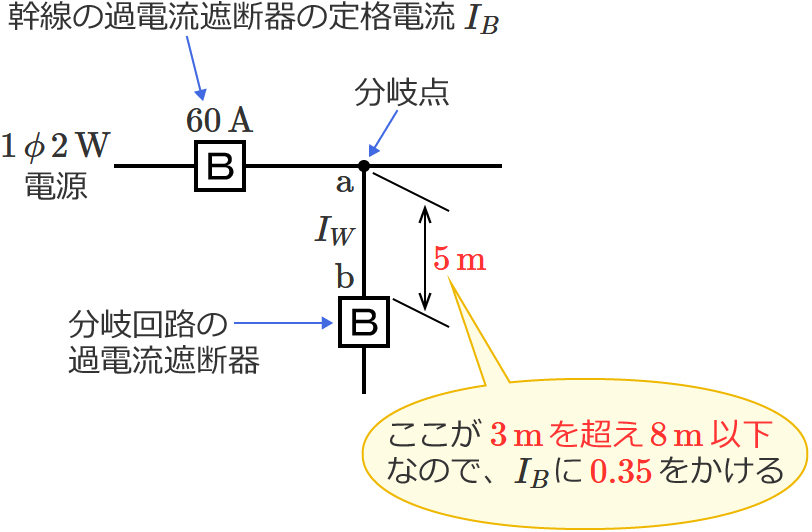
図のように定格電流 $\boldsymbol{60\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{5\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{21}$です。
問題の分岐回路の過電流遮断器は、分岐点から $5\,\mathrm{m}$ の位置に施設されます。$3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.35}\times I_B$ $=0.35\times 60$ $=21$ $\therefore\color{#f33}{21}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
問題5
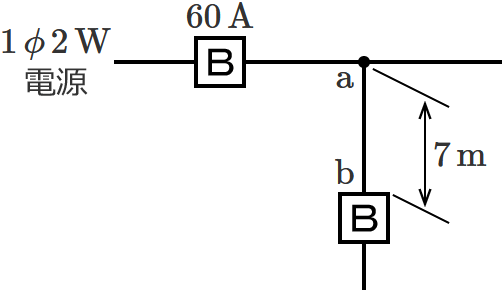
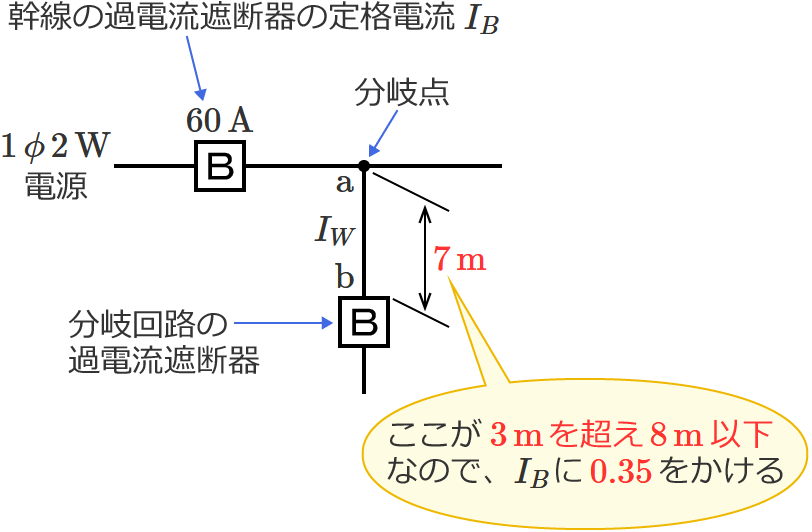
図のように定格電流 $\boldsymbol{60\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{7\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{21}$です。
問題の分岐回路の過電流遮断器は、分岐点から $7\,\mathrm{m}$ の位置に施設されます。$3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.35}\times I_B$ $=0.35\times 60$ $=21$ $\therefore\color{#f33}{21}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
スポンサーリンク
スポンサーリンク
問題6
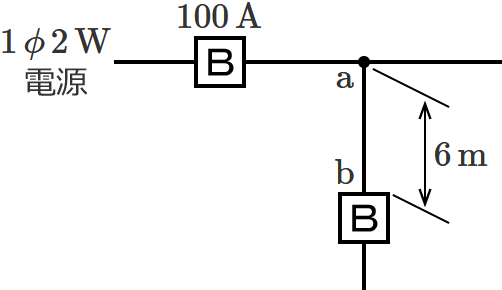
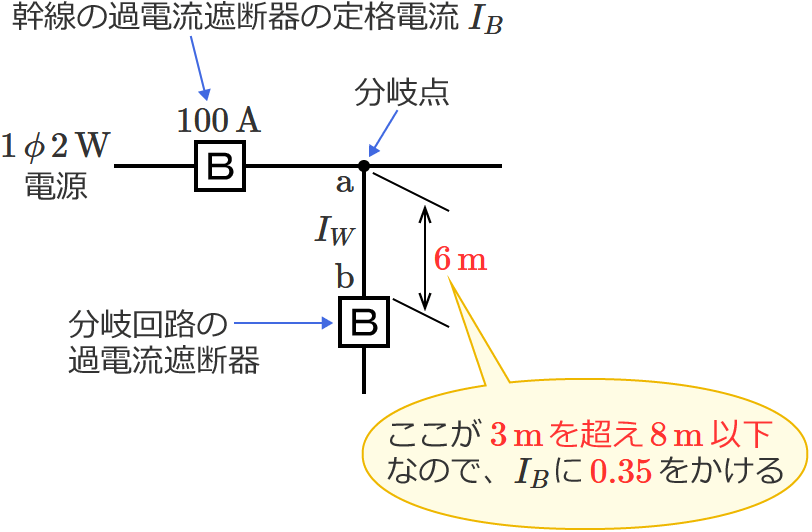
図のように定格電流 $\boldsymbol{100\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{6\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{35}$です。
問題の分岐回路の過電流遮断器は、分岐点から $6\,\mathrm{m}$ の位置に施設されます。$3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下の位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.35}\times I_B$ $=0.35\times 100$ $=35$ $\therefore\color{#f33}{35}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
問題7
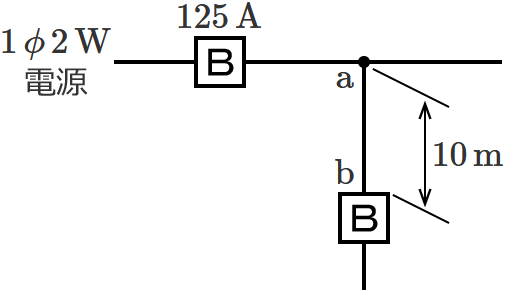
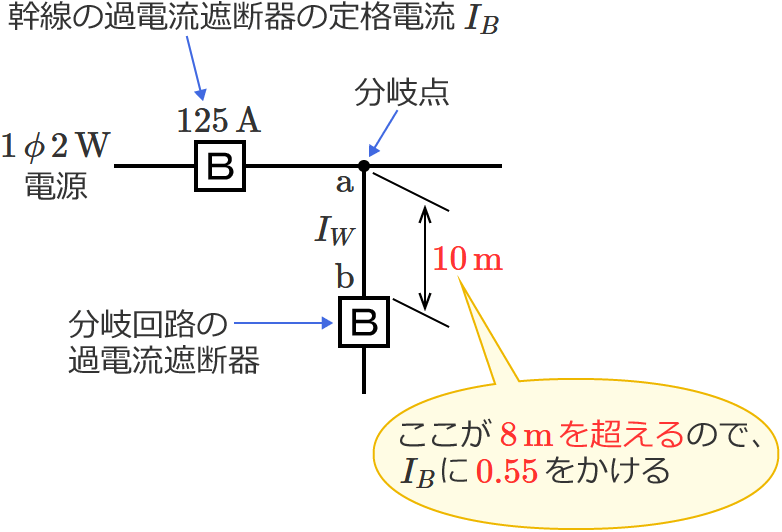
図のように定格電流 $\boldsymbol{125\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から分岐して、$\boldsymbol{10\,\mathrm{m}}$ の位置に過電流遮断器を施設するとき、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の電線の許容電流の最小値[$\boldsymbol{\mathrm{A}}$]は?
正解!
はずれ!
解説
正解は、$\boldsymbol{69}$です。
問題の分岐回路の過電流遮断器は、分岐点から $10\,\mathrm{m}$ の位置に施設されます。$8\,\mathrm{m}$ を超える位置に分岐回路の過電流遮断器を施設する場合は、「分岐点からの電線の許容電流 $I_W$ 」を「幹線の過電流遮断器の定格電流 $I_B$ 」の $55\,\%$ 以上にしなければなりません。
したがって、求める電線の許容電流 $I_W$ の最小値は、$I_W=\color{#f33}{0.55}\times I_B$ $=0.55\times 125$ $\fallingdotseq 69$ $\therefore\color{#f33}{69}\,\mathrm{A}$ になります。
| 分岐回路の過電流遮断器の施設位置 | 分岐点からの電線の許容電流の最小値 |
|---|---|
| $8\,\mathrm{m}$ を超える | $0.55\times$幹線の過電流遮断器の定格電流 |
| $3\,\mathrm{m}$ を超え $8\,\mathrm{m}$ 以下 | $0.35\times$幹線の過電流遮断器の定格電流 |
問題8
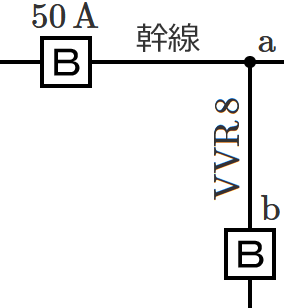
図のように定格電流 $\boldsymbol{50\,\mathrm{A}}$ の配線用遮断器で保護された低圧屋内幹線から $\boldsymbol{\mathrm{VVR}}$ ケーブル太さ $\boldsymbol{8\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{42\,\mathrm{A}}$ )で低圧屋内電路を分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さの最大値[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、ケーブルの許容電流を配線用遮断器の定格電流で割った値は、$\boldsymbol{42\div 50}$ $\boldsymbol{=0.84}$ になります。
正解!
はずれ!
解説
正解は、制限なしです。
幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ は $50\,\mathrm{A}$ 、分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ は $42\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=42\div 50$ $=0.84$ $=\color{#f33}{84\,\%}$ になります。
$I_W$ が $I_B$ の $55\,\%$ 以上の場合は、分岐回路の過電流遮断器を分岐点から $8\,\mathrm{m}$ を超える位置(制限なし)に施設できるので、求める $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値は「制限なし」になります。
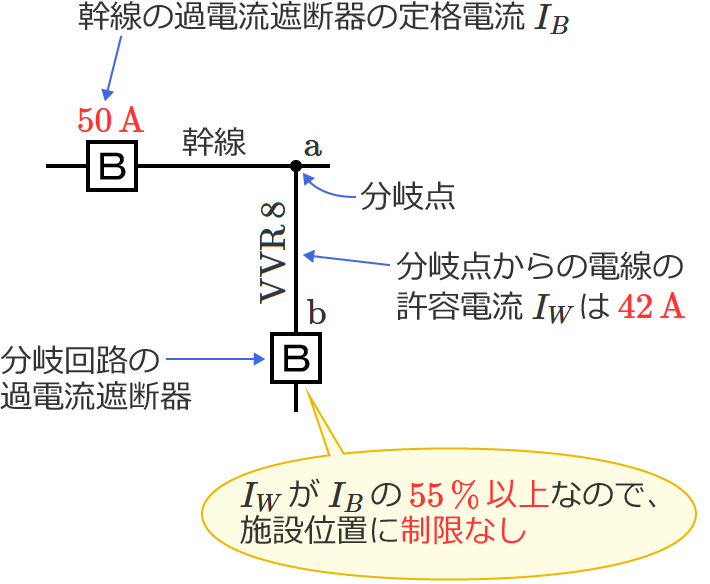
この問題8のような $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値を求める問題では、幹線の過電流遮断器の定格電流 $I_B$ に対する分岐点からの電線の許容電流 $I_W$ の割合( $I_W\div I_B$ の値)がポイントになります。
- 「分岐点からの電線の許容電流 $I_W$ 」が「幹線の過電流遮断器の定格電流 $I_B$ 」の $55\,\%$ 以上( $I_W\div I_B$ の値が $0.55$ 以上)の場合は、分岐回路の過電流遮断器の施設位置に制限なし(どこにでも施設できる)
- 「分岐点からの電線の許容電流 $I_W$ 」が「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 以上( $I_W\div I_B$ の値が $0.35$ 以上)の場合は、分岐回路の過電流遮断器を分岐点から $8\,\mathrm{m}$ 以下の位置に施設できる
- 「分岐点からの電線の許容電流 $I_W$ 」が「幹線の過電流遮断器の定格電流 $I_B$ 」の $35\,\%$ 未満( $I_W\div I_B$ の値が $0.35$ 未満)の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設する
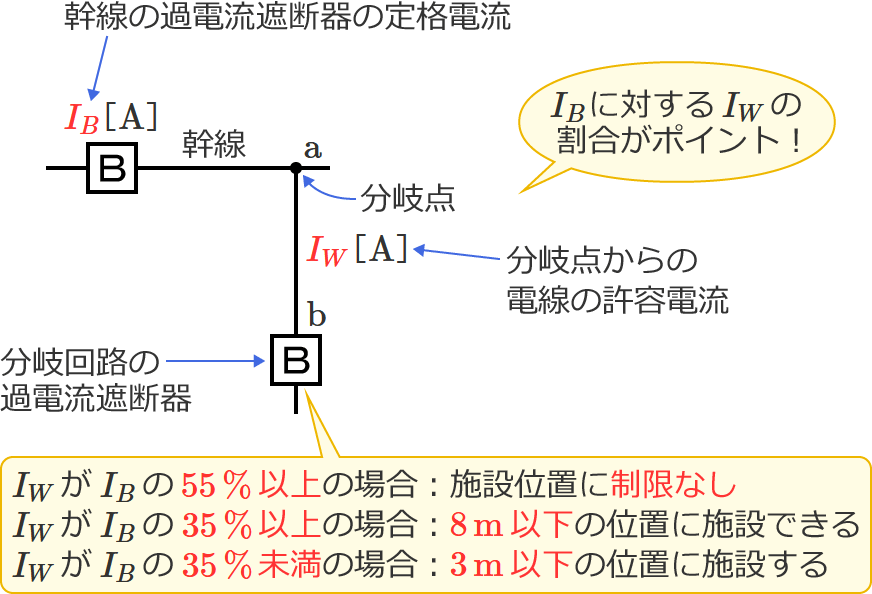
なので、$\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値を求める問題では、幹線の過電流遮断器の定格電流 $\boldsymbol{I_B}$ に対する分岐点からの電線の許容電流 $\boldsymbol{I_W}$ の割合( $I_W\div I_B$ の値)に着目しましょう!
問題9
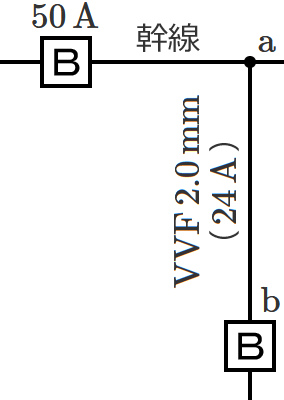
図のように、定格電流 $\boldsymbol{50\,\mathrm{A}}$ の過電流遮断器で保護される低圧屋内幹線から、太さ $\boldsymbol{2.0\,\mathrm{mm}}$ の $\boldsymbol{\mathrm{VVF}}$ ケーブル(許容電流 $\boldsymbol{24\,\mathrm{A}}$ )で分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さの最大値[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、ケーブルの許容電流を過電流遮断器の定格電流で割った値は、$\boldsymbol{24\div 50}$ $\boldsymbol{=0.48}$ になります。
正解!
はずれ!
解説
正解は、$\boldsymbol{8}$です。
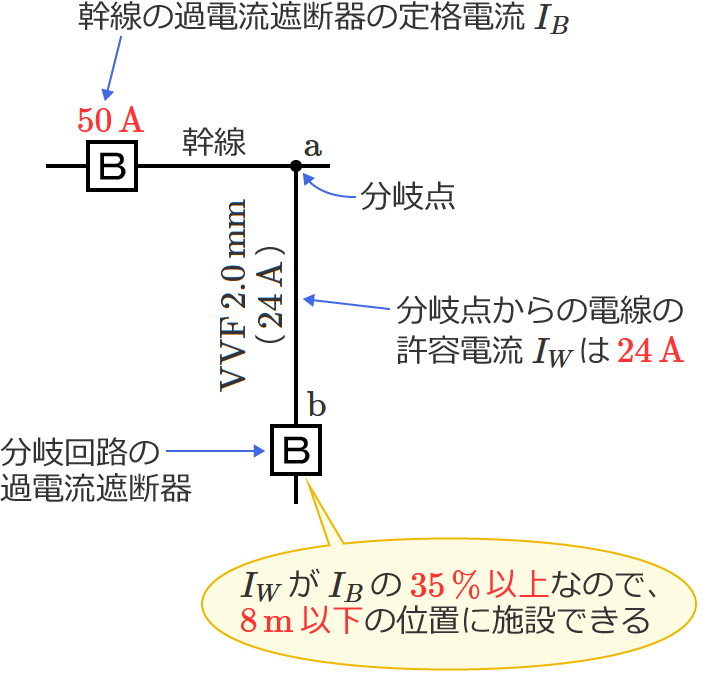
幹線の過電流遮断器の定格電流 $I_B$ は $50\,\mathrm{A}$ 、分岐点からの電線の許容電流( $\mathrm{VVF}$ ケーブルの許容電流)$I_W$ は $24\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=24\div 50$ $=0.48$ $=\color{#f33}{48\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 以上(ただし、$55\,\%$ 未満)の場合は、分岐回路の過電流遮断器を分岐点から $8\,\mathrm{m}$ 以下の位置に施設できるので、求める $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値は「 $8$ 」になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
問題10
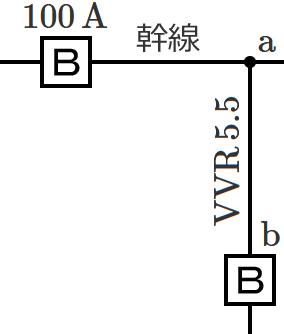
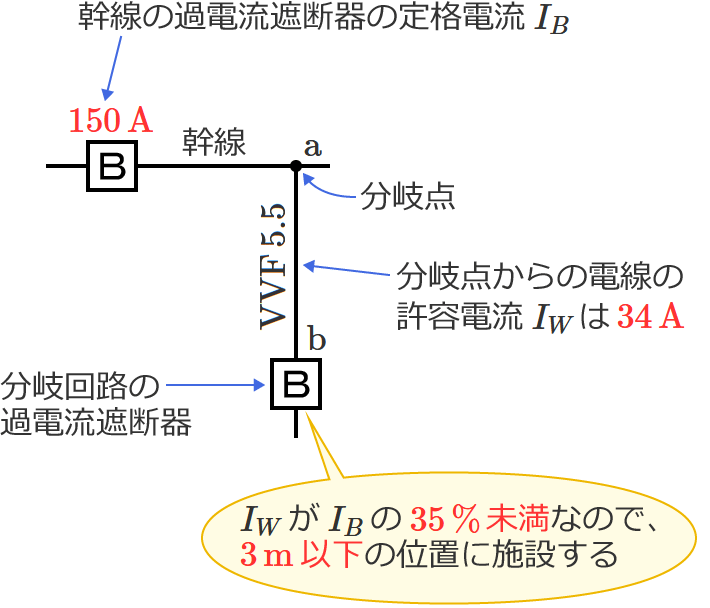
図のように、定格電流 $\boldsymbol{100\,\mathrm{A}}$ の配線用遮断器で保護された低圧屋内幹線から $\boldsymbol{\mathrm{VVR}}$ ケーブル太さ $\boldsymbol{5.5\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{34\,\mathrm{A}}$ )で低圧屋内電路を分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さの最大値[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、ケーブルの許容電流を配線用遮断器の定格電流で割った値は、$\boldsymbol{34\div 100}$ $\boldsymbol{=0.34}$ になります。
正解!
はずれ!
解説
正解は、$\boldsymbol{3}$です。
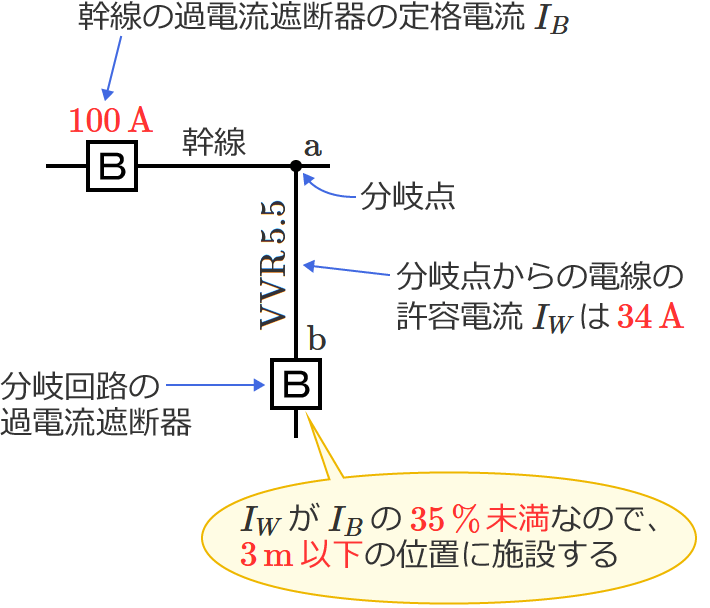
幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ は $100\,\mathrm{A}$ 、分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ は $34\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=34\div 100$ $=0.34$ $=\color{#f33}{34\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、求める $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値は「 $3$ 」になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
問題11
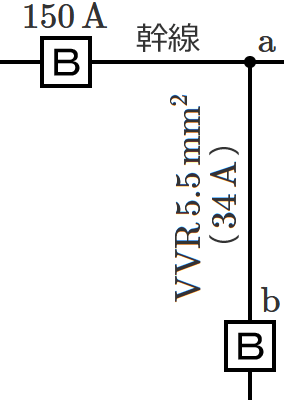
図のように定格電流 $\boldsymbol{150\,\mathrm{A}}$ の過電流遮断器で保護される低圧屋内幹線から、太さ $\boldsymbol{5.5\,\mathrm{mm^2}}$ の $\boldsymbol{\mathrm{VVR}}$ ケーブル(許容電流 $\boldsymbol{34\,\mathrm{A}}$ )で分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さの最大値[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、ケーブルの許容電流を過電流遮断器の定格電流で割った値は、$\boldsymbol{34\div 150}$ $\boldsymbol{\fallingdotseq 0.23}$ になります。
正解!
はずれ!
解説
正解は、$\boldsymbol{3}$です。
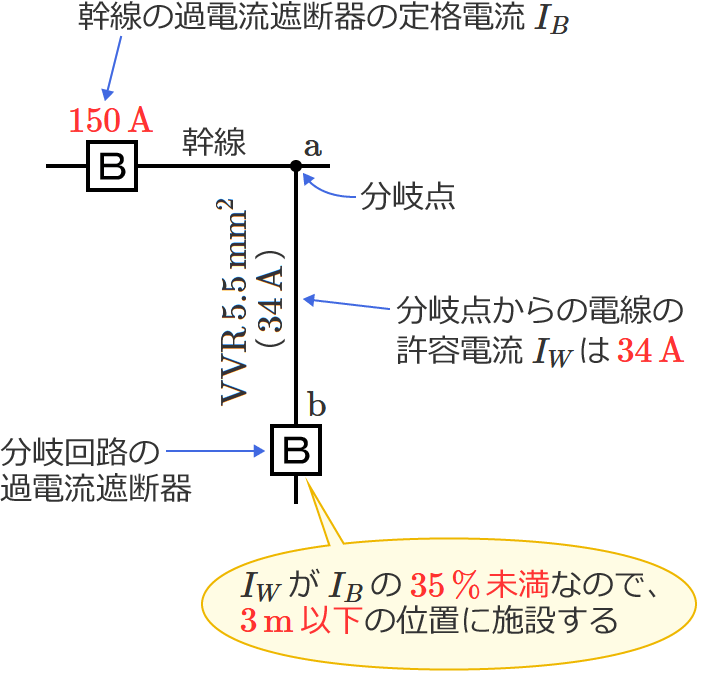
幹線の過電流遮断器の定格電流 $I_B$ は $150\,\mathrm{A}$ 、分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ は $34\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=34\div 150$ $\fallingdotseq 0.23$ $=\color{#f33}{23\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、求める $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値は「 $3$ 」になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
問題12
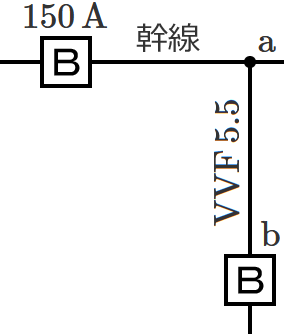
図のように定格電流 $\boldsymbol{150\,\mathrm{A}}$ の配線用遮断器で保護された低圧屋内幹線から太さ $\boldsymbol{5.5\,\mathrm{mm^2}}$ の $\boldsymbol{\mathrm{VVF}}$ ケーブル(許容電流 $\boldsymbol{34\,\mathrm{A}}$ )で低圧屋内電路を分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さの最大値[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、ケーブルの許容電流を配線用遮断器の定格電流で割った値は、$\boldsymbol{34\div 150}$ $\boldsymbol{\fallingdotseq 0.23}$ になります。
正解!
はずれ!
解説
正解は、$\boldsymbol{3}$です。
幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ は $150\,\mathrm{A}$ 、分岐点からの電線の許容電流( $\mathrm{VVF}$ ケーブルの許容電流)$I_W$ は $34\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=34\div 150$ $\fallingdotseq 0.23$ $=\color{#f33}{23\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、求める $\mathrm{a}$-$\mathrm{b}$ 間の長さの最大値は「 $3$ 」になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
問題13
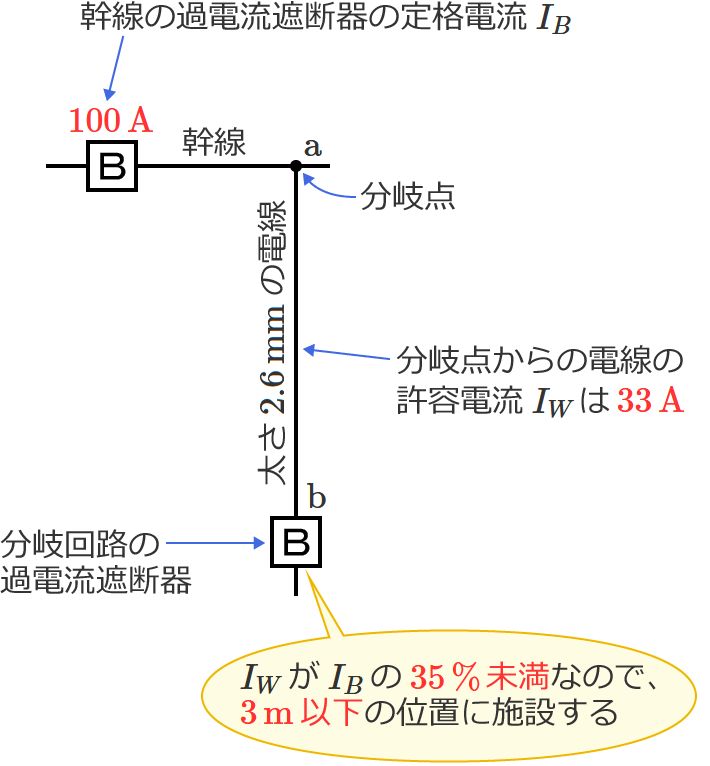
定格電流 $\boldsymbol{100\,\mathrm{A}}$ の過電流遮断器で保護された低圧屋内幹線から、太さ $\boldsymbol{2.6\,\mathrm{mm}}$ の電線(許容電流 $\boldsymbol{33\,\mathrm{A}}$ )で分岐回路を施設する場合、分岐点から配線用遮断器を施設する位置までの最大長さ[$\boldsymbol{\mathrm{m}}$]は? ただし、低圧屋内幹線に接続される負荷は、電灯負荷とする。
なお、電線の許容電流を過電流遮断器の定格電流で割った値は、$\boldsymbol{33\div 100}$ $\boldsymbol{=0.33}$ になります。
正解!
はずれ!
解説
正解は、$\boldsymbol{3}$です。
幹線の過電流遮断器の定格電流 $I_B$ は $100\,\mathrm{A}$ 、分岐点からの電線の許容電流(太さ $2.6\,\mathrm{mm}$ の電線の許容電流)$I_W$ は $33\,\mathrm{A}$ なので、$I_B$ に対する $I_W$ の割合は、$I_W\div I_B$ $=33\div 100$ $=0.33$ $=\color{#f33}{33\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器(配線用遮断器)を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、求める分岐点から配線用遮断器を施設する位置までの最大長さは「 $3$ 」になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
問題14
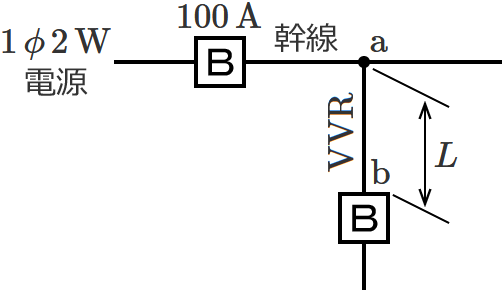
図のように、定格電流 $\boldsymbol{100\,\mathrm{A}}$ の配線用遮断器で保護された低圧屋内幹線から $\boldsymbol{\mathrm{VVR}}$ ケーブルで低圧屋内電路を分岐する場合、$\boldsymbol{\mathrm{a}}$-$\boldsymbol{\mathrm{b}}$ 間の長さ $\boldsymbol{L}$ と電線の太さ $\boldsymbol{A}$ の組合せとして、不適切なものは?
ただし、$\boldsymbol{\mathrm{VVR}}$ ケーブルの太さと許容電流の関係は表のとおりとする。
| 電線の太さ $A$ | 許容電流 |
|---|---|
| 直径 $2.0\,\mathrm{mm}$ | $24\,\mathrm{A}$ |
| 断面積 $5.5\,\mathrm{mm^2}$ | $34\,\mathrm{A}$ |
| 断面積 $8\,\mathrm{mm^2}$ | $42\,\mathrm{A}$ |
| 断面積 $14\,\mathrm{mm^2}$ | $61\,\mathrm{A}$ |
正解!
はずれ!
解説
正解は、$\boldsymbol{L}$:$\boldsymbol{10\,\mathrm{m}}$ $\boldsymbol{A}$:$\boldsymbol{8\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{42\,\mathrm{A}}$ )です。
●$\boldsymbol{L}$:$\boldsymbol{1\,\mathrm{m}}$ $\boldsymbol{A}$:$\boldsymbol{2.0\,\mathrm{mm}}$(許容電流 $\boldsymbol{24\,\mathrm{A}}$ )
電線の太さ $A$ が直径 $2.0\,\mathrm{mm}$ の電線の許容電流は表より $24\,\mathrm{A}$ なので、「幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ 」に対する「分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ 」の割合は、$I_W\div I_B$ $=24\div 100$ $=0.24$ $=\color{#f33}{24\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、$L$:$1\,\mathrm{m}$ の位置に施設できます。
したがって、$L$:$1\,\mathrm{m}$ $A$:$2.0\,\mathrm{mm}$ の組合せは適切です。
●$\boldsymbol{L}$:$\boldsymbol{2\,\mathrm{m}}$ $\boldsymbol{A}$:$\boldsymbol{5.5\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{34\,\mathrm{A}}$ )
電線の太さ $A$ が断面積 $5.5\,\mathrm{mm^2}$ の電線の許容電流は表より $34\,\mathrm{A}$ なので、「幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ 」に対する「分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ 」の割合は、$I_W\div I_B$ $=34\div 100$ $=0.34$ $=\color{#f33}{34\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 未満の場合は、分岐回路の過電流遮断器を分岐点から $3\,\mathrm{m}$ 以下の位置に施設するので、$L$:$2\,\mathrm{m}$ の位置に施設できます。
したがって、$L$:$2\,\mathrm{m}$ $A$:$5.5\,\mathrm{mm^2}$ の組合せは適切です。
●$\boldsymbol{L}$:$\boldsymbol{10\,\mathrm{m}}$ $\boldsymbol{A}$:$\boldsymbol{8\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{42\,\mathrm{A}}$ )
電線の太さ $A$ が断面積 $8\,\mathrm{mm^2}$ の電線の許容電流は表より $42\,\mathrm{A}$ なので、「幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ 」に対する「分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ 」の割合は、$I_W\div I_B$ $=42\div 100$ $=0.42$ $=\color{#f33}{42\,\%}$ になります。
$I_W$ が $I_B$ の $35\,\%$ 以上(ただし、$55\,\%$ 未満)の場合は、分岐回路の過電流遮断器を分岐点から $8\,\mathrm{m}$ 以下の位置に施設しなければならないので、$L$:$10\,\mathrm{m}$ の位置には施設できません。
したがって、$L$:$10\,\mathrm{m}$ $A$:$8\,\mathrm{mm^2}$ の組合せは不適切です。
●$\boldsymbol{L}$:$\boldsymbol{15\,\mathrm{m}}$ $\boldsymbol{A}$:$\boldsymbol{14\,\mathrm{mm^2}}$(許容電流 $\boldsymbol{61\,\mathrm{A}}$ )
電線の太さ $A$ が断面積 $14\,\mathrm{mm^2}$ の電線の許容電流は表より $61\,\mathrm{A}$ なので、「幹線の過電流遮断器(配線用遮断器)の定格電流 $I_B$ 」に対する「分岐点からの電線の許容電流( $\mathrm{VVR}$ ケーブルの許容電流)$I_W$ 」の割合は、$I_W\div I_B$ $=61\div 100$ $=0.61$ $=\color{#f33}{61\,\%}$ になります。
$I_W$ が $I_B$ の $55\,\%$ 以上の場合は、分岐回路の過電流遮断器の施設位置に制限はないので、$L$:$15\,\mathrm{m}$ の位置に施設できます。
したがって、$L$:$15\,\mathrm{m}$ $A$:$14\,\mathrm{mm^2}$ の組合せは適切です。
以上より、不適切なものは「$L$:$10\,\mathrm{m}$ $A$:$8\,\mathrm{mm^2}$(許容電流 $42\,\mathrm{A}$ )になります。
| $I_B$ に対する $I_W$ の割合 | 分岐回路の過電流遮断器の施設位置 |
|---|---|
| $55\,\%$ 以上 | 施設位置に制限なし |
| $35\,\%$ 以上 | $8\,\mathrm{m}$ 以下の位置に施設できる |
| $35\,\%$ 未満 | $3\,\mathrm{m}$ 以下の位置に施設する |
スポンサーリンク
スポンサーリンク
第二種電気工事士学科試験の4択クイズのまとめページ(一覧)はこちら
⇒ 第二種電気工事士学科試験の4択クイズ
2026年度の学科試験対策におすすめです!
このページの問題文には、(一財)電気技術者試験センターが作成した第二種電気工事士学科試験の試験問題から一部抜粋した文章を使用しています。
スポンサーリンク
第二種電気工事士学科試験の4択クイズ 分岐回路の開閉器および過電流遮断器の施設 関連ページ
- 4択クイズ 鑑別 スイッチ
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「スイッチ」についての4択クイズです。
- 4択クイズ 鑑別 コンセント
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「コンセント」についての4択クイズです。
- 4択クイズ 鑑別 遮断器と開閉器
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「遮断器と開閉器」についての4択クイズです。
- 4択クイズ 鑑別 照明器具
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「照明器具」についての4択クイズです。
- 4択クイズ 鑑別 電線管工事で使う材料
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電線管工事で使う材料」についての4択クイズです。
- 4択クイズ 鑑別 電線・ケーブルと電線を接続する材料
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電線・ケーブルと電線を接続する材料」についての4択クイズです。
- 4択クイズ 鑑別 その他の機器・器具・材料
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「その他の機器・器具・材料」についての4択クイズです。
- 4択クイズ 鑑別 電気工事で使う工具
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「電気工事で使う工具」についての4択クイズです。
- 4択クイズ 鑑別 測定器
- 第二種電気工事士学科試験の鑑別問題で出題されている内容について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。このページは「測定器」についての4択クイズです。
- 4択クイズ 接地工事
- 第二種電気工事士学科試験で出題されている「接地工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ ケーブル工事
- 第二種電気工事士学科試験で出題されている「ケーブル工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 地中埋設工事
- 第二種電気工事士学科試験で出題されている「地中埋設工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 金属管工事
- 第二種電気工事士学科試験で出題されている「金属管工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 金属可とう電線管工事
- 第二種電気工事士学科試験で出題されている「金属可とう電線管工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 合成樹脂管工事
- 第二種電気工事士学科試験で出題されている「合成樹脂管工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 金属線ぴ工事
- 第二種電気工事士学科試験で出題されている「金属線ぴ工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 金属・フロア・ライティングダクト工事
- 第二種電気工事士学科試験で出題されている「金属ダクト工事、フロアダクト工事、ライティングダクト工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ ネオン放電灯工事
- 第二種電気工事士学科試験で出題されている「ネオン放電灯工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ ショウウィンドー・ショウケース内工事
- 第二種電気工事士学科試験で出題されている「ショウウィンドー・ショウケース内工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 小勢力回路の工事
- 第二種電気工事士学科試験で出題されている「小勢力回路の工事」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 低圧屋内配線工事と施工できる場所
- 第二種電気工事士学科試験で出題されている「低圧屋内配線工事と施工できる場所」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 特殊な場所の工事と施工できる場所
- 第二種電気工事士学科試験で出題されている「特殊な場所の工事と施工できる場所」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 三相誘導電動機のスターデルタ始動法
- 第二種電気工事士学科試験で出題されている「三相誘導電動機のスターデルタ始動法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 三相誘導電動機を逆回転させる方法
- 第二種電気工事士学科試験で出題されている「三相誘導電動機を逆回転させる方法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 三相誘導電動機の力率改善
- 第二種電気工事士学科試験で出題されている「三相誘導電動機の力率改善」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 計器に表示されている記号
- 第二種電気工事士学科試験で出題されている「計器に表示されている記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電圧、電流、電力、力率の測定回路
- 第二種電気工事士学科試験で出題されている「電圧、電流、電力、力率の測定回路」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ クランプ形の電流計による電流の測定
- 第二種電気工事士学科試験で出題されている「クランプ形の電流計による電流の測定」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 接地抵抗計と接地抵抗の測定方法
- 第二種電気工事士学科試験で出題されている「接地抵抗計と接地抵抗の測定方法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 絶縁抵抗計と絶縁抵抗の測定
- 第二種電気工事士学科試験で出題されている「絶縁抵抗計と絶縁抵抗の測定」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 回路計(テスタ)
- 第二種電気工事士学科試験で出題されている「回路計(テスタ)」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 検電器
- 第二種電気工事士学科試験で出題されている「検電器」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 竣工検査
- 第二種電気工事士学科試験で出題されている「竣工検査」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気設備技術基準・解釈
- 第二種電気工事士学科試験で出題されている「電気設備技術基準・解釈」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気事業法
- 第二種電気工事士学科試験で出題されている「電気事業法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気工事士法
- 第二種電気工事士学科試験で出題されている「電気工事士法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気工事業法
- 第二種電気工事士学科試験で出題されている「電気工事業法(電気工事業の業務の適正化に関する法律)」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気用品安全法
- 第二種電気工事士学科試験で出題されている「電気用品安全法」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電線の許容電流
- 第二種電気工事士学科試験で出題されている「電線の許容電流」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 幹線の太さを決める根拠となる電流の最小値
- 第二種電気工事士学科試験で出題されている「幹線の太さを決める根拠となる電流の最小値」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 配線の図記号
- 第二種電気工事士学科試験で出題されている「配線の図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 絶縁電線・ケーブルの記号
- 第二種電気工事士学科試験で出題されている「絶縁電線・ケーブルの記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電線管・ダクトの記号
- 第二種電気工事士学科試験で出題されている「電線管・ダクトの記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ スイッチの図記号
- 第二種電気工事士学科試験で出題されている「スイッチの図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ コンセントの図記号
- 第二種電気工事士学科試験で出題されている「コンセントの図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 遮断器と開閉器の図記号
- 第二種電気工事士学科試験で出題されている「遮断器と開閉器の図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 照明器具の図記号
- 第二種電気工事士学科試験で出題されている「照明器具の図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 電気機器・計器の図記号
- 第二種電気工事士学科試験で出題されている「電気機器・計器の図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ ボックスなどその他の図記号
- 第二種電気工事士学科試験で出題されている「ボックスなどその他の図記号」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ コンセントの刃受の形状(極配置)
- 第二種電気工事士学科試験で出題されている「コンセントの刃受の形状(極配置)」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 最少電線本数(心線数)
- 第二種電気工事士学科試験で出題されている「最少電線本数(心線数)」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 配線工事に必要なケーブル
- 第二種電気工事士学科試験で出題されている「配線工事に必要なケーブル」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ 差込形コネクタの種類と最少個数の組合せ
- 第二種電気工事士学科試験で出題されている「使用する差込形コネクタの種類と最少個数の組合せ」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ リングスリーブの種類と最少個数の組合せ
- 第二種電気工事士学科試験で出題されている「使用するリングスリーブの種類と最少個数の組合せ」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。
- 4択クイズ リングスリーブの種類、個数、刻印の組合せ
- 第二種電気工事士学科試験で出題されている「使用するリングスリーブの種類、個数および刻印の組合せ」について4択クイズ(一問一答)にしてみました。スマホでもできるので(たぶん)、ちょっとしたスキマ時間などにポチポチやってみるのもいいかもです。



