スポンサーリンク



倍率器

※ページ内にPR･広告が含まれる場合があります。

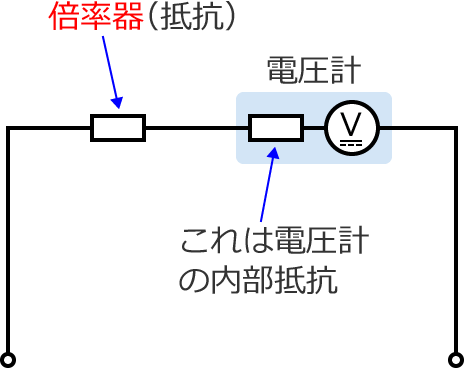
電圧計の測定範囲を拡大するために、電圧計に直列に接続する抵抗を倍率器といいます。

 

倍率器

 

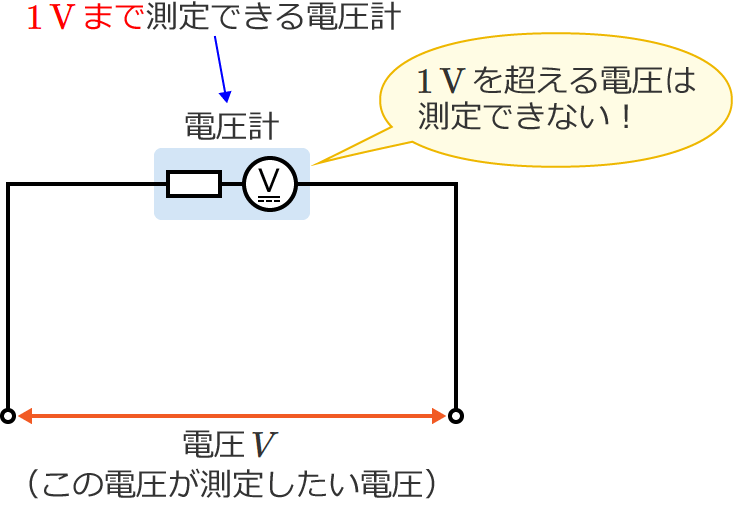
例えば、$1\,\mathrm{V}$ まで測定できる電圧計があるとして、これをそのまま使うと $1\,\mathrm{V}$ を超える電圧は測定できません。

 

この電圧計だけでは1Vまでしか測定できない

 

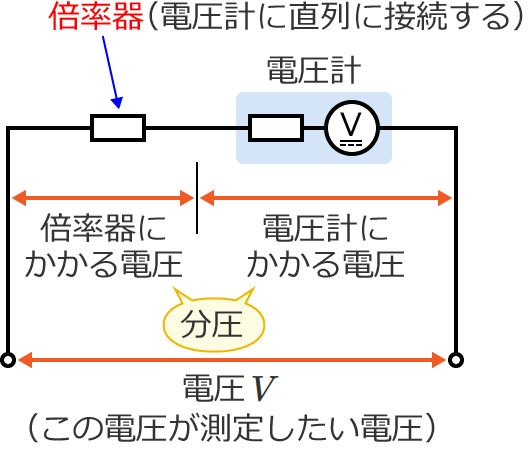
ですが、この電圧計に直列に倍率器（抵抗）を接続すると、電圧 $V$ は電圧計と倍率器に分圧するので、

 

電圧Vは電圧計と倍率器に分圧する

 

電圧 $V$ が $1\,\mathrm{V}$ を超えても電圧を測定できるようになります。

 

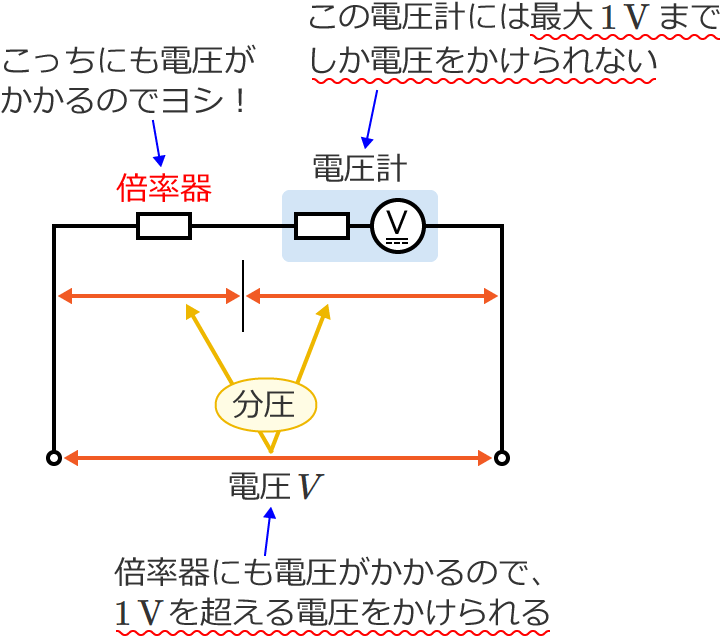
倍率器があるので1Vを超える電圧をかけることができる

 

例えば、電圧計に $1\,\mathrm{V}$ の電圧がかかるときに倍率器には $99\,\mathrm{V}$ の電圧がかかるように倍率器の抵抗値を決めれば、$100\,\mathrm{V}$ までの電圧をかけることができるようになるので、

 

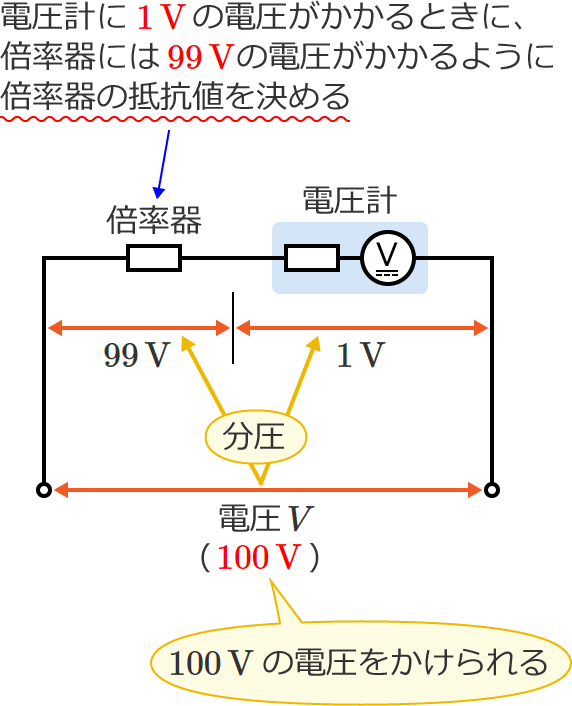
100Vまでの電圧をかけることができる

 

$1\,\mathrm{V}$ までしか測定できない電圧計を使って $100\,\mathrm{V}$ まで測定できるようになります。（電圧計の測定範囲が100倍に拡大される！）

 

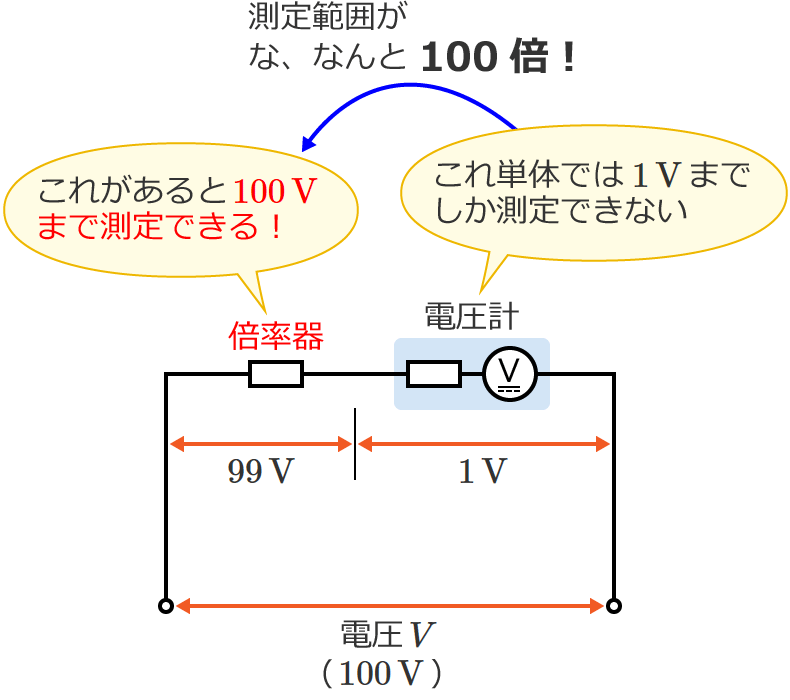
倍率器によって測定範囲が拡大された

 

このように、電圧計の測定範囲を拡大するために使われるのが倍率器です。

 

分圧については、こちらの直流回路の計算（分圧と分流）のページを参考にしてみてください。

 

スポンサーリンク

スポンサーリンク


 

倍率器の倍率

次のように、内部抵抗 $r_v$［$\Omega$］の電圧計に直列に抵抗 $R_m$［$\Omega$］の倍率器が接続された回路があるとします。

 

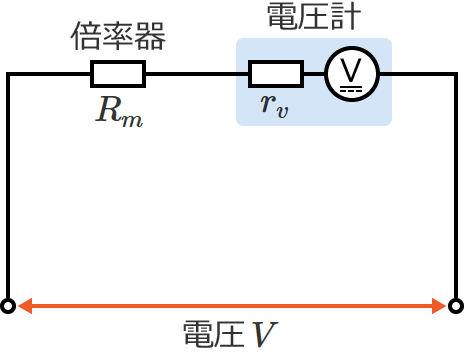
倍率器を接続した回路

 

この回路において、電圧 $V$［$\mathrm{V}$］と電圧計にかかる電圧 $V_v$［$\mathrm{V}$］の比の値 $m=\dfrac{V}{V_v}$ を求めてみます。

 

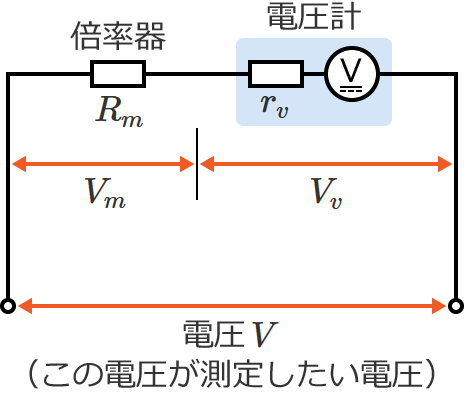
電圧Vと電圧計にかかる電圧Vv

 

電圧計にかかる電圧 $V_v$ は、分圧の公式より次のように求められます。

 

$V_v=V\times\dfrac{r_v}{r_v+R_m}$　…①

 

この①式から $m\left( =\dfrac{V}{V_v}\right)$ を求めると、

 

$\dfrac{V_v}{V} =\dfrac{r_v}{r_v+R_m}$

 

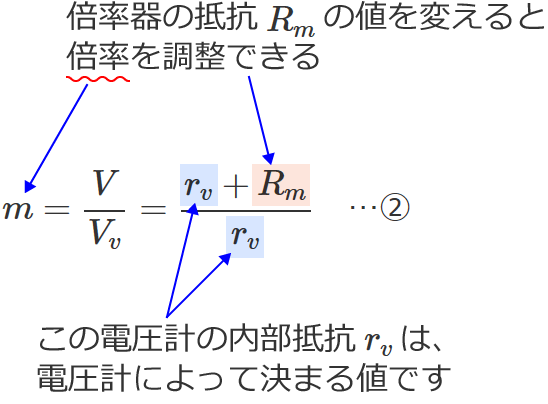
$\therefore\, m=\dfrac{V}{V_v} =\dfrac{r_v+R_m}{r_v}$　…②

 

となります。

 

この②式の $m$ の値は、$V$ を $V_v$ で割ったものなので、「電圧 $V$ 」が「電圧計にかかる電圧 $V_v$ 」の何倍になるかを表わしています。

 

つまり、②式から求められる値 $m$ は、倍率器を接続することによって電圧計の測定範囲が何倍になるか（ $m$ 倍になる）を表わす値になり、この値 $m$ を倍率器の倍率といいます。

 

倍率器の倍率

 

また、②式の倍率器の倍率 $m$ は「電圧計の内部抵抗 $r_v$ 」と「倍率器の抵抗 $R_m$ 」で表わされているので、電圧計の測定範囲を拡大するときの倍率は、倍率器の抵抗 $R_m$ の値を変えることで調整できることになります。（電圧計の内部抵抗 $r_v$ は、電圧計によって決まる値です。）

 

倍率器の抵抗の値を変えると倍率を調整できる

 

電圧計の測定範囲をm倍に拡大するときの倍率器の抵抗値の求め方

電圧計の測定範囲を $m$ 倍に拡大するときの倍率器の抵抗値 $R_m$ は、さきほどの②式を使うと求められます。

 

$m=\dfrac{V}{V_v} =\dfrac{r_v+R_m}{r_v}$　…②　（この式を使う）

 

②式を $R_m=\cdots$ の形に変形すると、

 

$m\, r_v=r_v+R_m$

 

$R_m=m\, r_v-r_v$

 

$\therefore\, R_m=\left( m-1\right) r_v$　…③

 

となります。

 

なので、③式に倍率 $m$ と電圧計の内部抵抗 $r_v$ の値を代入すると、電圧計の測定範囲を $m$ 倍に拡大するときの倍率器の抵抗値 $R_m$ が求められます。

 

電圧計の測定範囲をm倍にするときの倍率器の抵抗値

 

電圧計の測定範囲を拡大するときの倍率器の抵抗値の計算例

内部抵抗 $r_v$ が $3\,\mathrm{k}\Omega$ の電圧計の測定範囲を $100$ 倍にするとき、倍率器の抵抗値 $R_m$ は？

 

$R_m=\left( m-1\right) r_v$ $=\left( 100-1\right)\times 3000$ $=99\times 3000=297000$

 

$\therefore$ 倍率器の抵抗値 $R_m=297\,\mathrm{k}\Omega$

 

倍率器のまとめ
  • 電圧計の測定範囲を拡大するために、電圧計に直列に接続する抵抗を倍率器という
  • 倍率器の倍率 $m$： $m=\dfrac{V}{V_v} =\dfrac{r_v+R_m}{r_v}$
  • 電圧計の測定範囲を $m$ 倍にするときの倍率器の抵抗値 $R_m$： $R_m=\left( m-1\right) r_v$

 

スポンサーリンク

スポンサーリンク


 

電流計の測定範囲を拡大するときは、分流器を使います。分流器については、こちらの分流器のページを参考にしてみてください。

分流器　←BACK

NEXT→　電圧降下法



スポンサーリンク


倍率器　関連ページ

分流器
分流器について解説しています。分流器は電流計に並列に接続する抵抗で、電流計の測定範囲を拡大するときに使われます。
電圧降下法
電圧降下法（電位降下法）について解説しています。電圧降下法は、電圧計と電流計を使って抵抗にかかる電圧と抵抗に流れる電流を測定し、その測定値から抵抗を測定する（求める）測定方法です。
ホイートストンブリッジ
ホイートストンブリッジについて解説しています。ホイートストンブリッジは、未知の抵抗値を測定するときによく使われている回路です。