スポンサーリンク
ホイートストンブリッジ
※ページ内にPR・広告が含まれる場合があります。
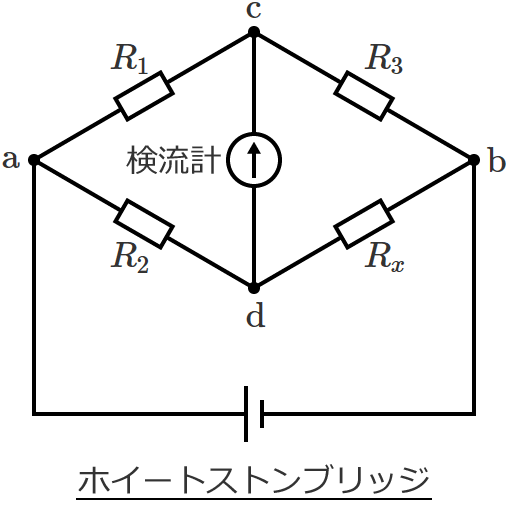
次のように、直列接続された2つの抵抗が並列に接続されている回路があるとして、
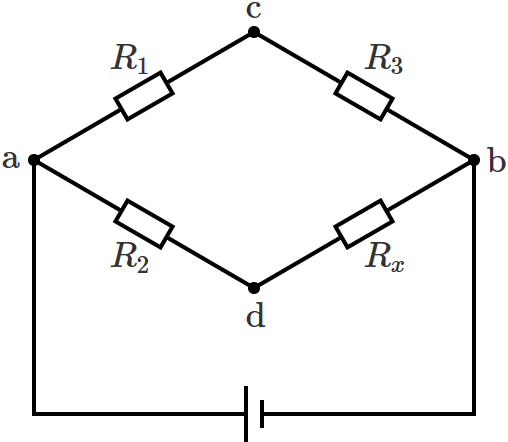
この回路の $\mathrm{c}$-$\mathrm{d}$ 間に検流計を接続した次のような回路をホイートストンブリッジといいます。
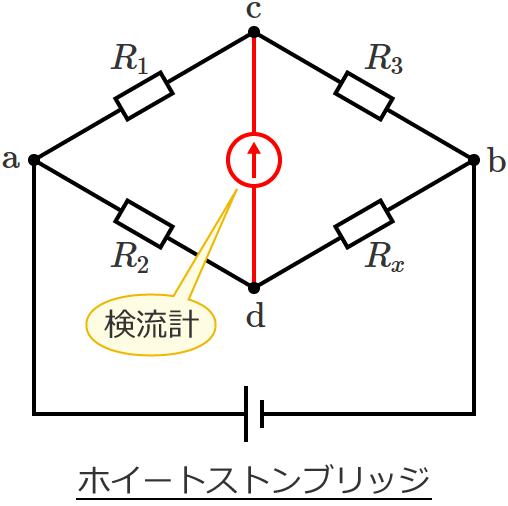
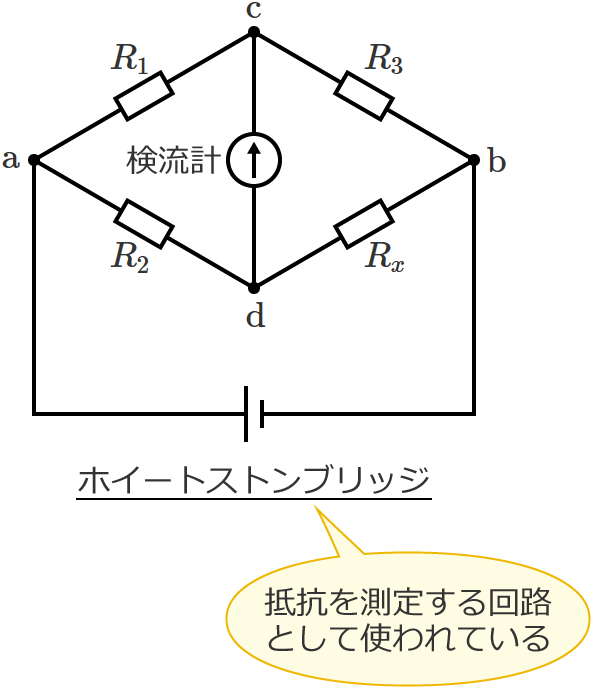
このホイートストンブリッジは、ブリッジの平衡条件から未知の抵抗の値を求めることができるので、抵抗を測定する回路として広く使われています。
スポンサーリンク
ホイートストンブリッジが平衡するための条件
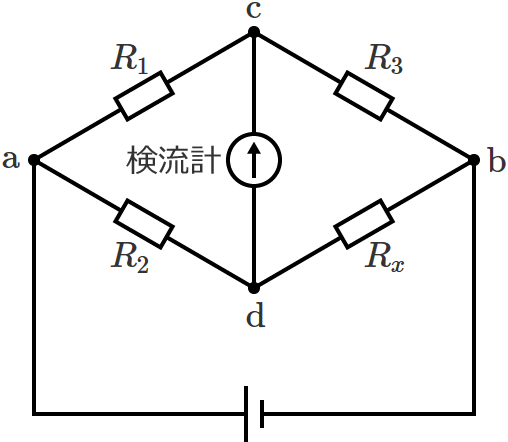
ホイートストンブリッジ回路の4つの抵抗の値を適当に調整すると、検流計に流れる電流をゼロにすることができ、このときの状態(検流計に電流が流れていない状態)をブリッジが平衡しているといいます。
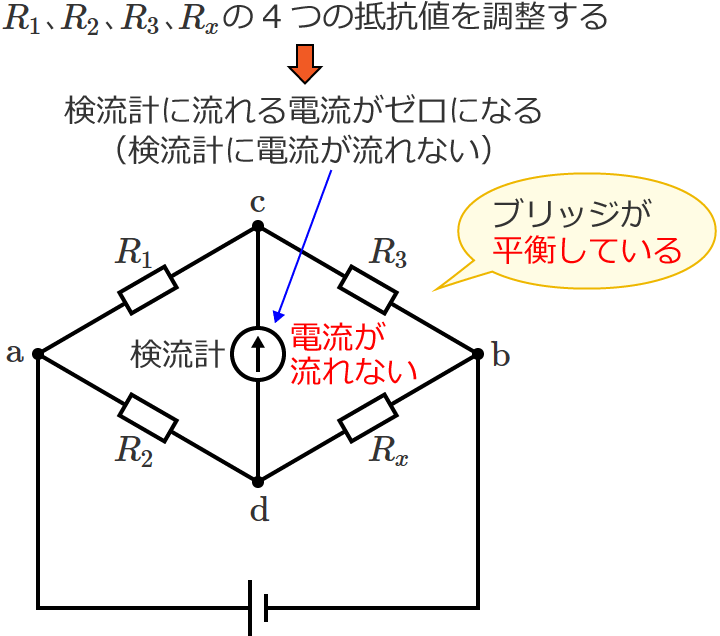
ホイートストンブリッジが平衡するための条件は、次のように求めることができます。
ブリッジが平衡しているときは検流計に電流が流れないので、抵抗 $R_1$ に流れる電流を $I_1$ とすると抵抗 $R_3$ に流れる電流も $I_1$ になります。また、同じように、抵抗 $R_2$ に流れる電流を $I_2$ とすると抵抗 $R_x$ に流れる電流も $I_2$ になります。
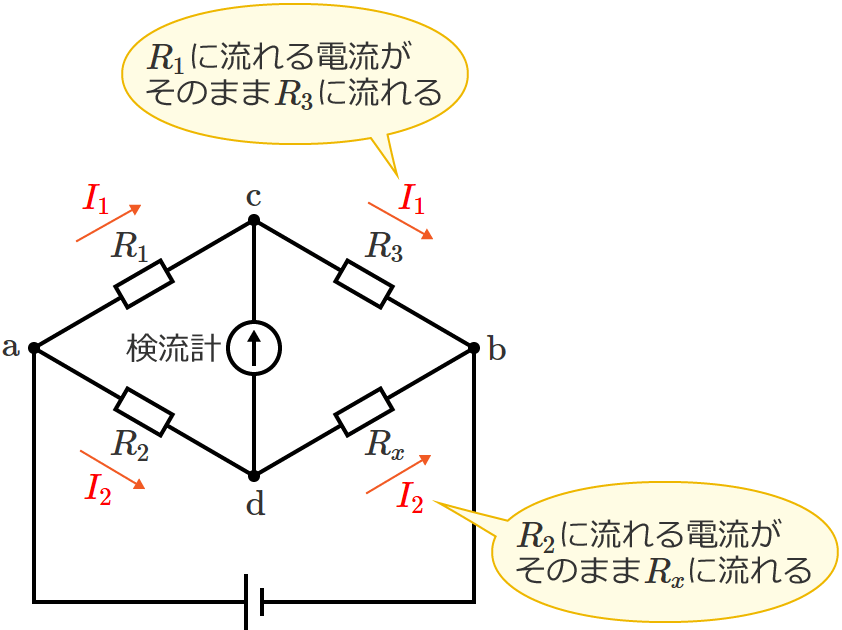
このとき、回路の $\mathrm{a}$-$\mathrm{c}$-$\mathrm{d}$-$\mathrm{a}$ の閉路をループ❶、$\mathrm{c}$-$\mathrm{b}$-$\mathrm{d}$-$\mathrm{c}$ の閉路をループ❷とすると、
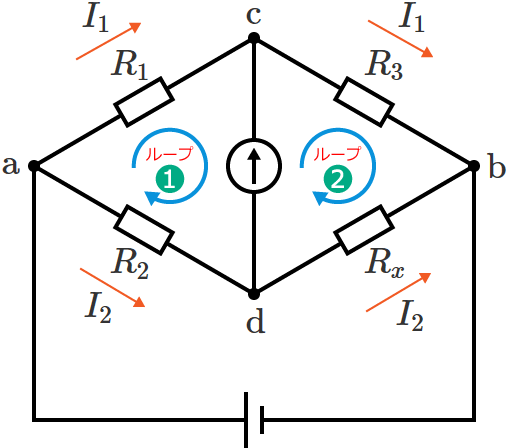
キルヒホッフの第二法則より、
ループ❶では、
$R_1\, I_1-R_2\, I_2=0$
$R_1\, I_1=R_2\, I_2$
$\therefore\, \dfrac{I_1}{I_2} =\dfrac{R_2}{R_1}$ …③
ループ❷では、
$R_3\, I_1-R_x\, I_2=0$
$R_3\, I_1=R_x\, I_2$
$\therefore\, \dfrac{I_1}{I_2} =\dfrac{R_x}{R_3}$ …④
となります。したがって、③$\, =\,$④ とすると、
$\dfrac{R_2}{R_1} =\dfrac{R_x}{R_3}$
$\therefore\, R_1\, R_x=R_2\, R_3$ …⑤ (ホイートストンブリッジが平衡するための条件)
となり、これがホイートストンブリッジが平衡するための条件になります。
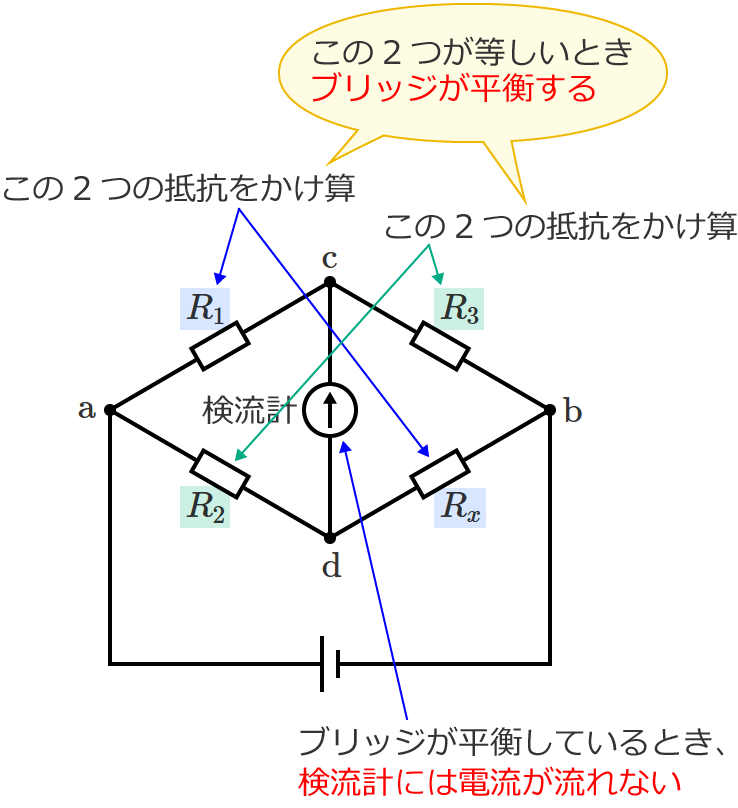
⑤式をみると分かるように、向かい合う辺の抵抗の値をかけたものどうしが等しくなるとき、ホイートストンブリッジが平衡します。
スポンサーリンク
スポンサーリンク
ホイートストンブリッジによる未知の抵抗の値の求め方
ホイートストンブリッジが平衡しているとき(検流計に電流が流れていないとき)は、さきほどの⑤式より、
$R_1\, R_x=R_2\, R_3$ (ホイートストンブリッジが平衡するときの条件)
が成り立つので、この原理を利用すると未知の抵抗の値を測定することができます。
次のように、抵抗の値が分かっている2つの抵抗 $R_1$、$R_2$、抵抗の値を変えることができる可変抵抗 $R_3$、抵抗の値が分からない未知の抵抗 $R_x$ からなるホイートストンブリッジ回路があるとします。
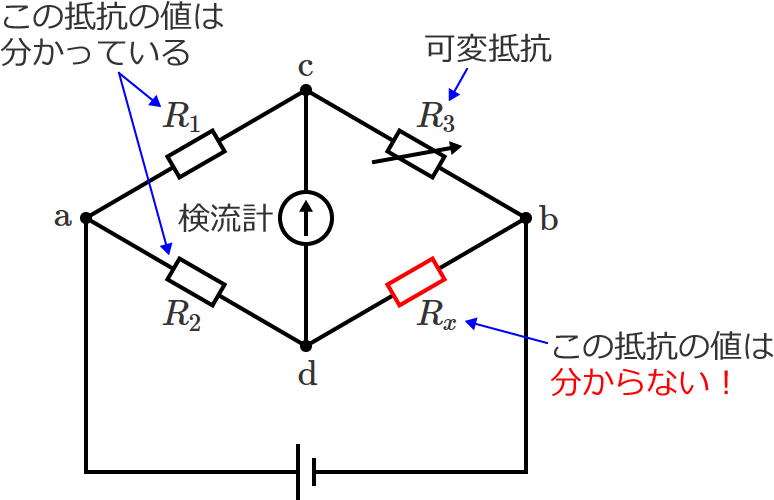
この回路において、可変抵抗 $R_3$ の値を適当に調整して、検流計に電流が流れないようにします。(つまり、ブリッジが平衡している状態にします。)
すると、ブリッジが平衡しているので、ブリッジの平衡条件 $R_1\, R_x=R_2\, R_3$ が成り立ちます。この平衡条件の式を $R_x=\cdots$ に変形すると、
$R_x=\dfrac{R_2}{R_1} R_3$ …⑥
となるので、この⑥式に各値( $R_1$、$R_2$、$R_3$ )を代入すると未知の抵抗 $R_x$ の値を求めることができます。
このようにホイートストンブリッジを使うと未知の抵抗値を測定でき、また、検流計の内部抵抗の影響も受けずに精密に抵抗の測定ができるので、ホイートストンブリッジは、$1\,\Omega$ から $1\, \mathrm{M}\Omega$ 程度の抵抗の測定に広く使われています。
- 検流計に流れる電流がゼロになっている状態をブリッジが平衡しているという
- ホイートストンブリッジが平衡するときの条件: $R_1\, R_x=R_2\, R_3$
- ホイートストンブリッジを使うと、抵抗を測定できる
スポンサーリンク
スポンサーリンク
電圧降下法 ←BACK
NEXT→ 電気のお勉強のTOP
スポンサーリンク


