スポンサーリンク
電圧降下法
※ページ内にPR・広告が含まれる場合があります。
電圧計で抵抗にかかる電圧、電流計で抵抗に流れる電流を測定し、その測定値から抵抗を求める方法を電圧降下法といいます。電圧降下法は、電位降下法ともいいます。
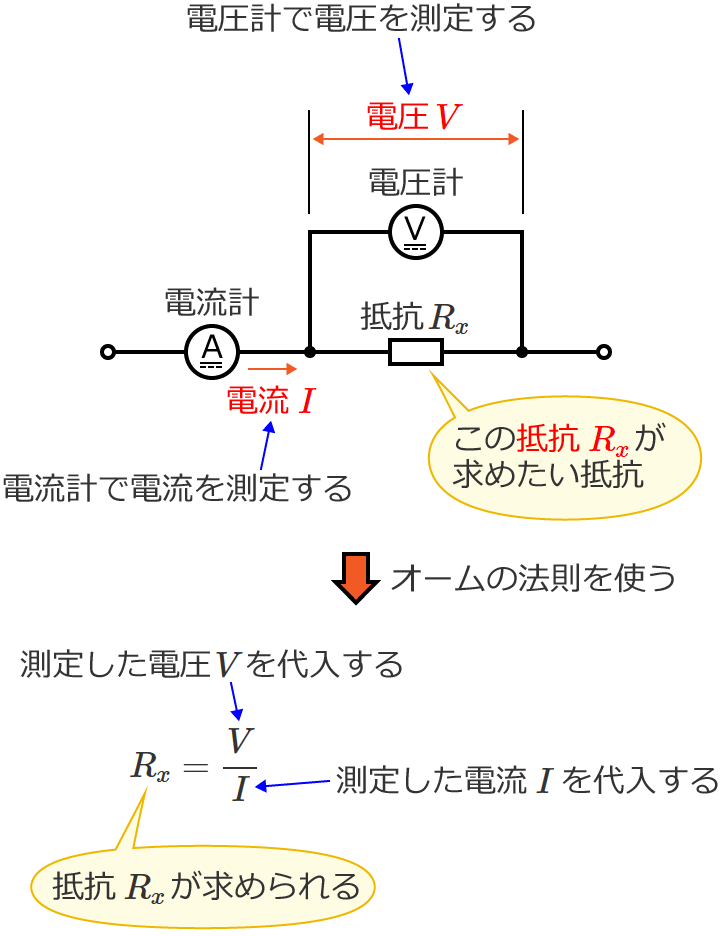
この電圧降下法による抵抗の測定は、電圧と電流を測定してオームの法則を使って抵抗を算出するだけなので、比較的簡単に抵抗の測定ができます。
ただし、電圧計と電流計には内部抵抗があるため、
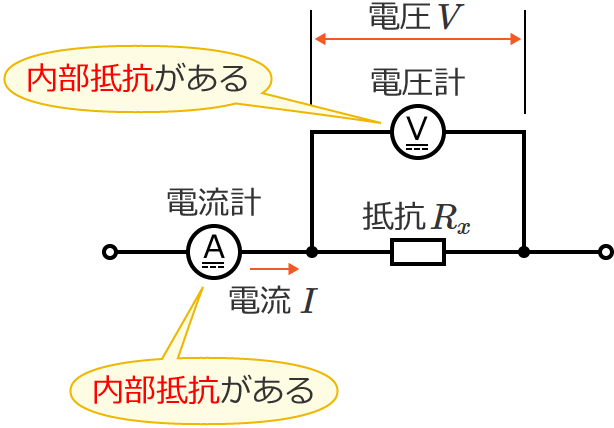
それらの内部抵抗を考慮しない場合には、大きな誤差が生じる場合があります。
スポンサーリンク
電圧降下法における電圧計と電流計の接続方法と誤差
電圧降下法で抵抗を測定するときの電圧計と電流計の接続方法には、次の2通りの接続方法があります。
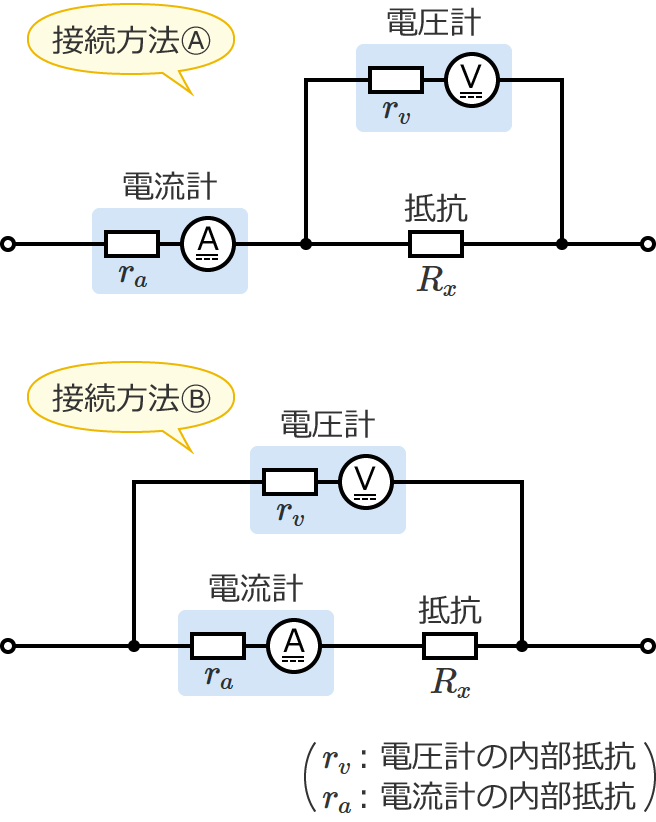
この2通りの接続方法のどちらでも抵抗を測定することはできますが、測定する抵抗の大きさによって、Ⓐの接続方法にした方が誤差が小さくなる場合と、Ⓑの接続方法にした方が誤差が小さくなる場合があります。( $R_x=V/I$ で抵抗を求める場合)
測定する抵抗 Rx << 電圧計の内部抵抗 rv の場合
測定する抵抗の値を $R_x$、電圧計の内部抵抗の値を $r_v$ としたとき、$R_x\ll r_v$( $R_x$ が $r_v$ より十分小さい)の場合は、Ⓐの接続方法で測定した方が誤差が小さくなります。
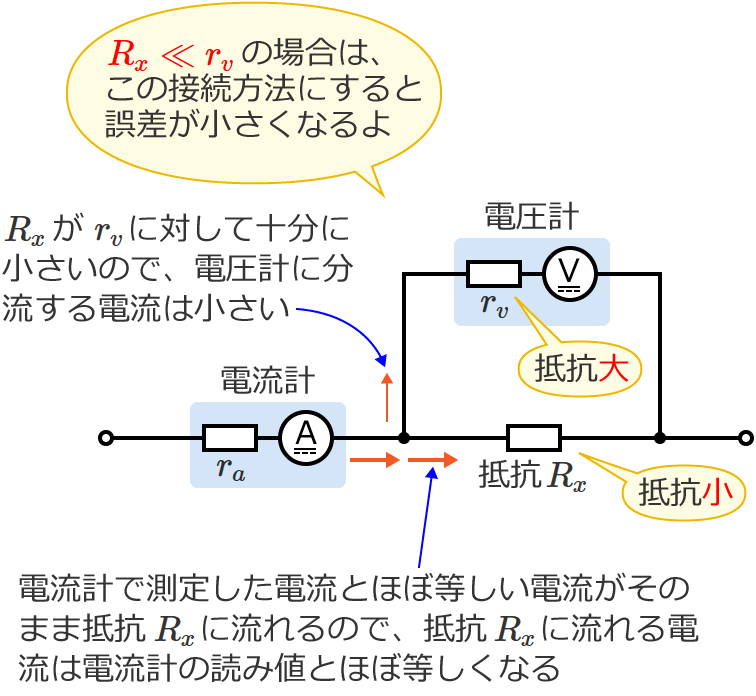
ちなみに、$R_x\ll r_v$( $R_x$ が $r_v$ より十分小さい)で、$R_x$ が $r_a$ に対して十分大きくない場合にⒷの接続方法で測定すると、$r_a$ にかかる電圧 $V_a$ が無視できないくらいの大きさになるので誤差が大きくなります。
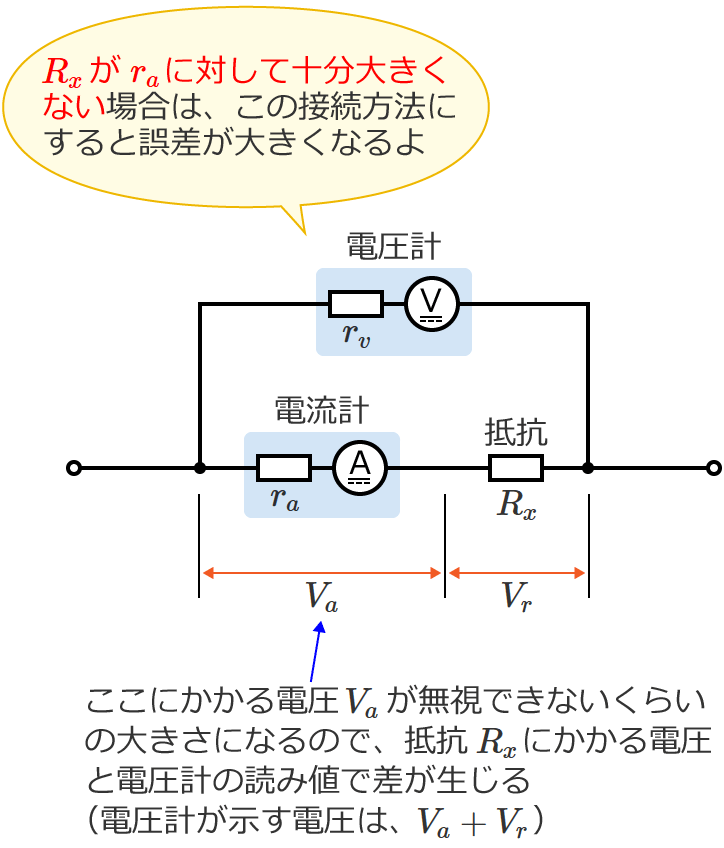
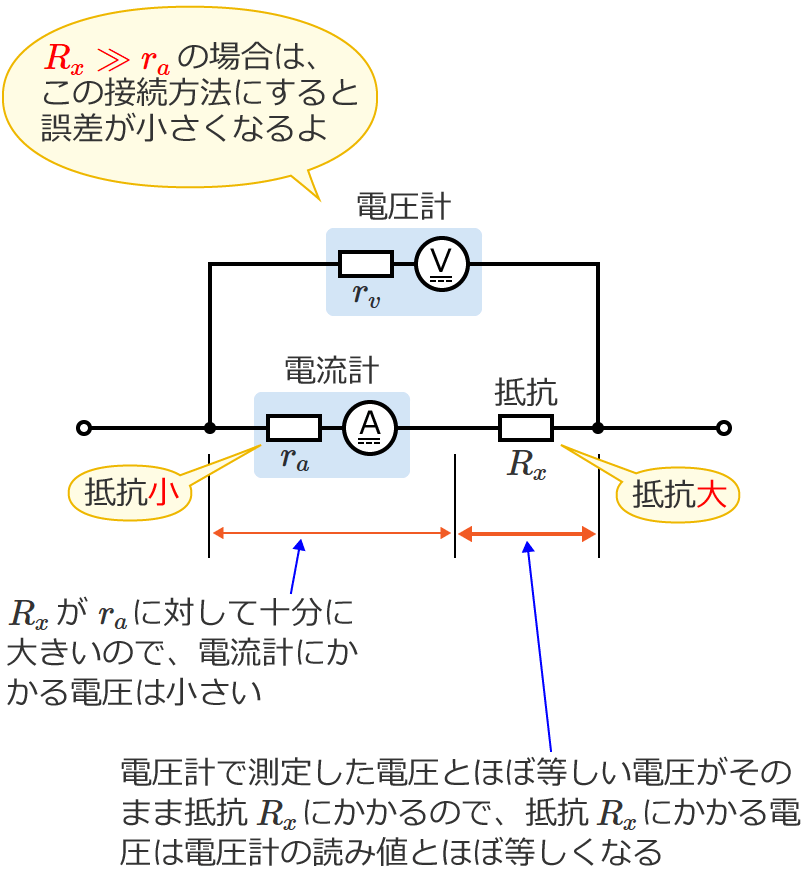
測定する抵抗 Rx >> 電流計の内部抵抗 ra の場合
測定する抵抗の値を $R_x$、電流計の内部抵抗の値を $r_a$ としたとき、$R_x\gg r_a$( $R_x$ が $r_a$ より十分大きい)の場合は、Ⓑの接続方法で測定した方が誤差が小さくなります。
ちなみに、$R_x\gg r_a$( $R_x$ が $r_a$ より十分大きい)で、$R_x$ が $r_v$ に対して十分小さくない場合にⒶの接続方法で測定すると、電圧計に分流する電流 $I_v$ が無視できないくらいの大きさになるので誤差が大きくなります。
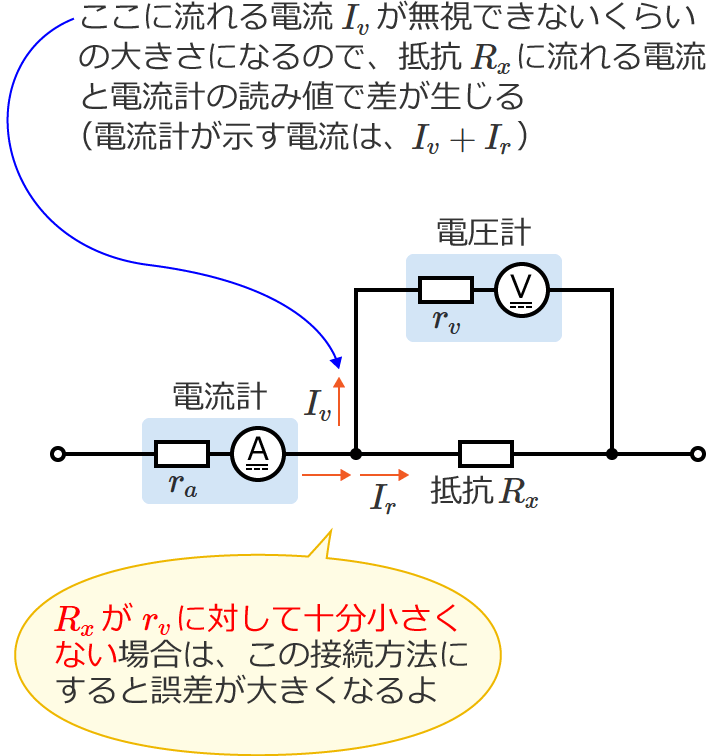
スポンサーリンク
スポンサーリンク
測定する抵抗 Rx の値をより正確に求める場合
測定する抵抗 $R_x$ の値をより正確に求める場合は、次のようにします。
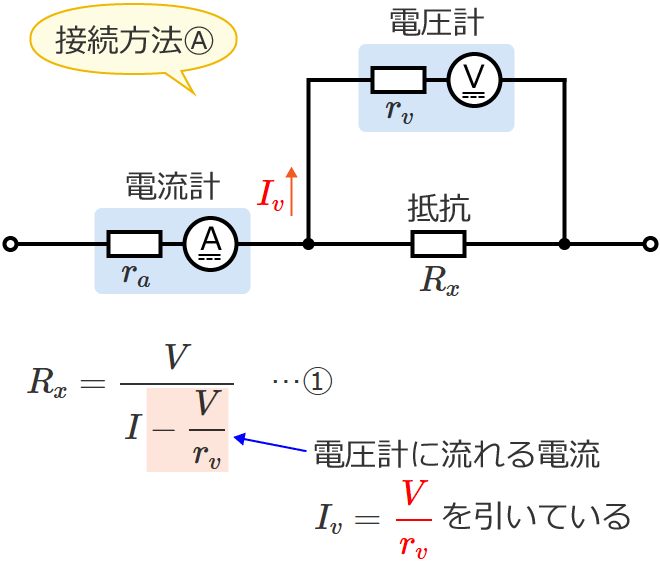
接続方法Ⓐの場合
接続方法Ⓐで測定した場合は、電圧計で測定した電圧 $V$、電流計で測定した電流 $I$、電圧計の内部抵抗 $r_v$ を次の①式に代入して抵抗 $R_x$ を求めます。
$R_x=\dfrac{V}{I-\dfrac{V}{r_v}}$ …①
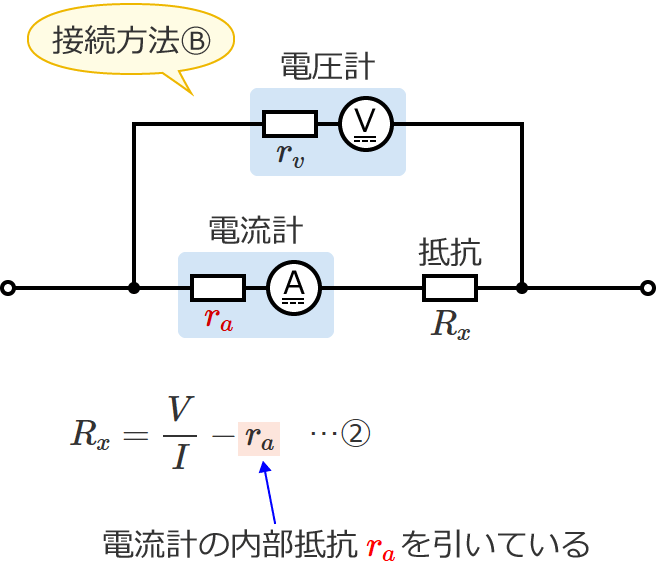
接続方法Ⓑの場合
接続方法Ⓑで測定した場合は、電圧計で測定した電圧 $V$、電流計で測定した電流 $I$、電流計の内部抵抗 $r_a$ を次の②式に代入して抵抗 $R_x$ を求めます。
$R_x=\dfrac{V}{I} -r_a$ …②
①、②式には電圧計と電流計の内部抵抗が考慮されているので、①、②式を使えば、$R_x=\dfrac{V}{I}$ の式を使って抵抗 $R_x$ を求めるよりも、より正確に抵抗 $R_x$ を求めることができます。
- 電圧計と電流計で電圧と電流を測定し、その測定値から抵抗を求める方法を電圧降下法という
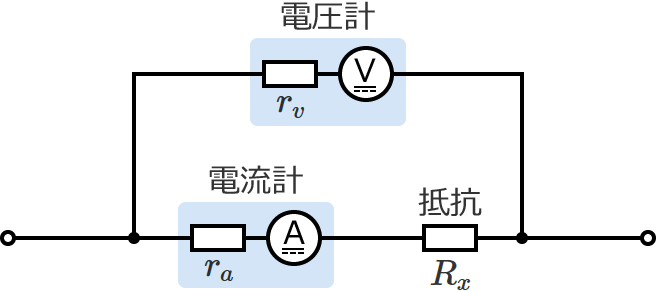
- $R_x\ll r_v$ の場合は、次の接続方法で測定すると誤差が小さくなる
より正確に求めたい場合は、
$R_x=\dfrac{V}{I-\dfrac{V}{r_v}}$ の式を使う
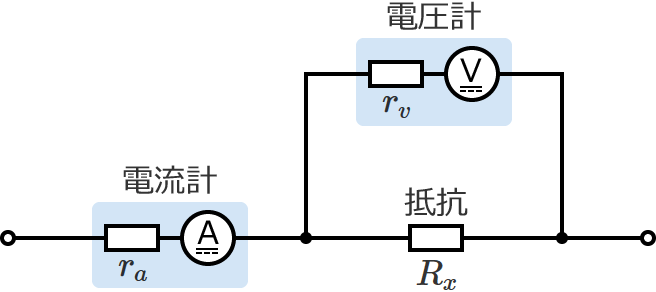
- $R_x\gg r_a$ の場合は、次の接続方法で測定すると誤差が小さくなる
より正確に求めたい場合は、
$R_x=\dfrac{V}{I} -r_a$ の式を使う
スポンサーリンク
スポンサーリンク
倍率器 ←BACK
NEXT→ ホイートストンブリッジ
スポンサーリンク
電圧降下法 関連ページ
- 分流器
- 分流器について解説しています。分流器は電流計に並列に接続する抵抗で、電流計の測定範囲を拡大するときに使われます。
- 倍率器
- 倍率器について解説しています。倍率器は電圧計に直列に接続する抵抗で、電圧計の測定範囲を拡大するときに使われます。
- ホイートストンブリッジ
- ホイートストンブリッジについて解説しています。ホイートストンブリッジは、未知の抵抗値を測定するときによく使われている回路です。


