抵抗を示す式を求める計算問題の解き方

※ページ内にPR･広告が含まれる場合があります。

第二種電気工事士学科試験の抵抗を示す式を求める計算問題の解き方について解説しています。

第二種電気工事士学科試験を受験する方の中には、

計算問題が苦手！とか、

計算問題はもう捨てちゃいました！（捨てないで～）

という方もいるかもしれませんが、第二種電気工事士学科試験で出題されている計算問題のほとんどは、

過去に出題された計算問題とまったく同じ問題
過去に出題された計算問題の数値を変えただけの問題
ちょっとだけ何か（？）を変えた類似問題

で、出題項目ごとに過去問題を見てみると、問題の出題パターンもほぼ同じです。

ですので、計算問題が苦手な方でも、出題項目ごとにおぼえることをおぼえて解き方のパターンに慣れてしまえば、計算問題でも点数をとれるようになります。

このページでは、過去に試験で出題された過去問題を使って抵抗を示す式を求める計算問題の解き方について解説していますので、このページを読んで抵抗を示す式を求める計算問題を解けるようになりましょう。

計算問題も解けるようになると、合格がぐぐぐーん！と近づきますよ！

問題には過去問題を使っていますので、過去問題の勉強にもなると思います。

抵抗を示す式を求める計算問題を解くための基礎知識
オームの法則の公式
電力の公式
抵抗を示す式を求める計算問題（過去問題）と解き方
問題1
出題：令和3年度上期午前問2

抵抗を示す式を求める計算問題を解くための基礎知識

まず初めに、抵抗を示す式を求める計算問題を解くためにおぼえておかなければならないことをおぼえてしまいましょう。

抵抗を示す式を求める計算問題を解けるようになるためにおぼえておかなければならないのは、次の電気の基本的な公式です。

オームの法則の公式
電力の公式

この公式さえおぼえておけば、あとはどこでこの公式を使うのか（どこにこの公式を当てはめるのか）だけです。

オームの法則の公式

オームの法則の公式は次のような公式で、電気回路の電圧、電流、抵抗の関係を表わす公式です。

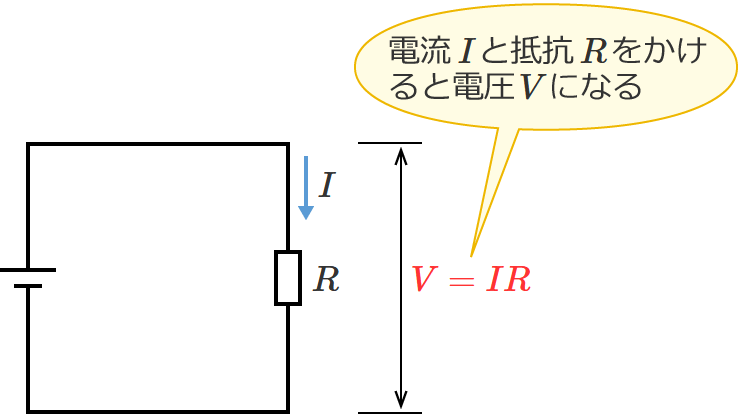
オームの法則の公式：$V=IR$　…①

①式の $V$ は電圧［$\mathrm{V}$］、$I$ は電流［$\mathrm{A}$］、$R$ は抵抗［$\Omega$］を表わし、①式は、電流（$I$）と抵抗（$R$）をかけたものは電圧（$V$）になりますよ、という式です。（電流と抵抗が分かれば、電圧が分かる。）

オームの法則の公式（V=IR）

ここで、①式を $I=\cdots$ の式に変形すると次のような式になり、

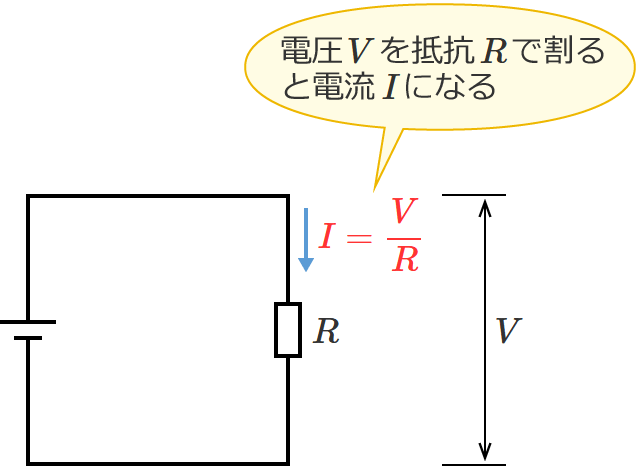
$I=\dfrac{V}{R}$　…②

この②式は、電圧（$V$）を抵抗（$R$）で割ったものは電流（$I$）になりますよ、という式になります。（電圧と抵抗が分かれば、電流が分かる。）

オームの法則の公式（I=V/R）

また、①式を $R=\cdots$ の式に変形すると次のような式になり、

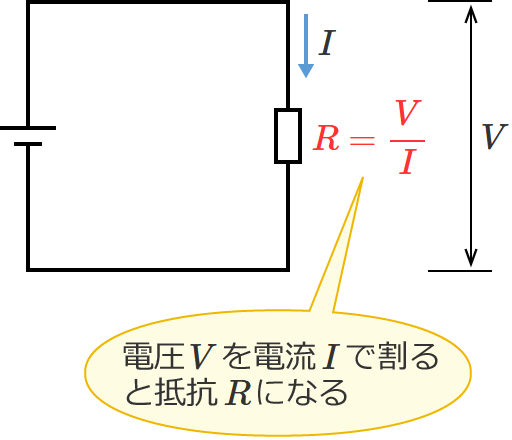
$R=\dfrac{V}{I}$　…③

この③式は、電圧（$V$）を電流（$I$）で割ったものは抵抗（$R$）になりますよ、という式になります。（電圧と電流が分かれば、抵抗が分かる。）

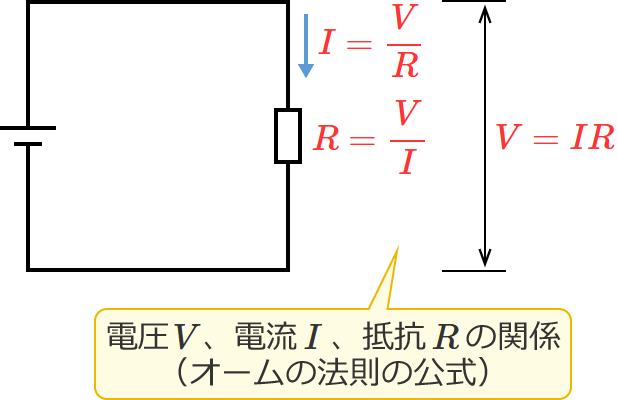
オームの法則の公式（R=V/I）

これら3つの式（①式、②式、③式）は、抵抗を示す式を求める計算問題を解くときだけではなく電気回路の計算をするときによく使われるので、必ずおぼえておきましょう！

オームの法則の公式

電力の公式

電力の公式は次のような公式で、抵抗で消費される電力（消費電力）を表わす公式です。

電力（消費電力）の公式：$P=VI$　…④

④式の $V$ は電圧［$\mathrm{V}$］、$I$ は電流［$\mathrm{A}$］、$P$ は電力［$\mathrm{W}$］を表わし、④式は、電圧（$V$）と電流（$I$）をかけたものは電力（$P$）になりますよ、という式です。（電圧と電流が分かれば、電力（消費電力）が分かる。）

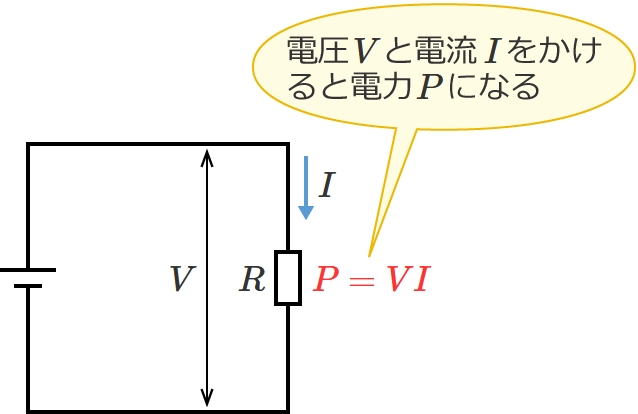
電力の公式（P=VI）

ここで、④式に先ほどのオームの法則の①式（ $V=IR$ ）を代入すると次のような式（⑤式）になり、

$P=VI$　（④式）

$=\color{#ff3333}{IR}\times I$　（$V$ に $IR$ を代入した）

$\therefore P=I^2R$　…⑤

この⑤式は、電流の2乗（$I^2$）に抵抗（$R$）をかけたものは電力（$P$）になりますよ、という式になります。（電流と抵抗が分かれば、電力（消費電力）が分かる。）

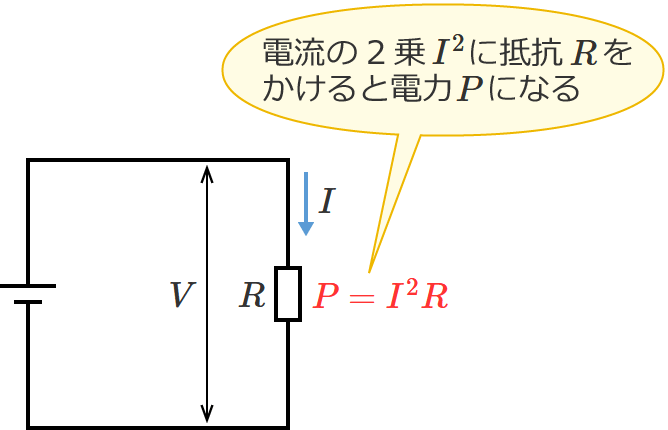
電力の公式（P=I^2×R）

また、④式に先ほどのオームの法則の②式（ $I=\dfrac{V}{R}$ ）を代入すると次のような式（⑥式）になり、

$P=VI$　（④式）

$=V\times \color{#ff3333}{\dfrac{V}{R}}$　（$I$ に $\dfrac{V}{R}$ を代入した）

$\therefore P=\dfrac{V^2}{R}$　…⑥

この⑥式は、電圧の2乗（$V^2$）を抵抗（$R$）で割ったものは電力（$P$）になりますよ、という式になります。（電圧と抵抗が分かれば、電力（消費電力）が分かる。）

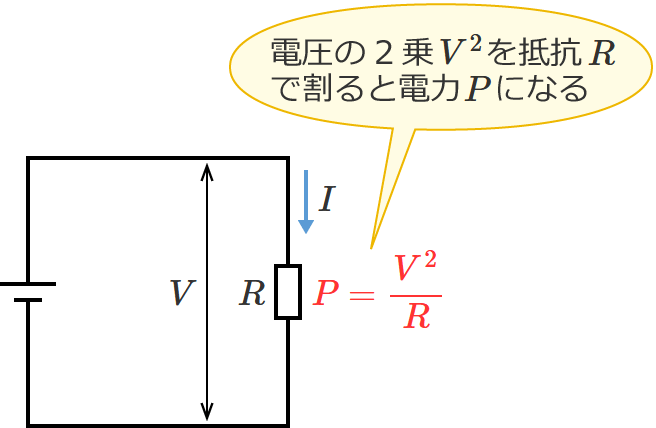
電力の公式（P=V^2/R）

これら3つの式（④式、⑤式、⑥式）も、抵抗を示す式を求める計算問題を解くときだけではなく電気回路の計算をするときによく使われるので、必ずおぼえておきましょう！

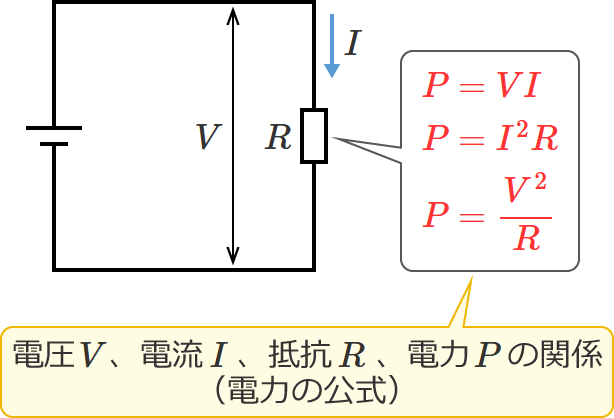
電力の公式

以上の「オームの法則の公式（3つ）」と「電力の公式（3つ）」をおぼえたら、抵抗を示す式を求める計算問題を解くための基礎知識はOKです！（このページに掲載している問題は、6つの公式すべて使わなくても解けるんですけどね。）

では、過去に第二種電気工事士学科試験で出題された過去問題を解いてみましょう！

補足

公式は2つだけおぼえておけば大丈夫！

ここの解説でおぼえる公式を6つあげましたが、解説を読んでみると分かるように、6つの公式は2つの公式をもとにつくられています。

なので、式の変形や代入などの計算が苦手でなければ、公式を6つ丸暗記する必要はなく、次の2つの公式だけおぼえておけば大丈夫です。

$V=IR$　（オームの法則の公式）
$P=VI$　（電力の公式）

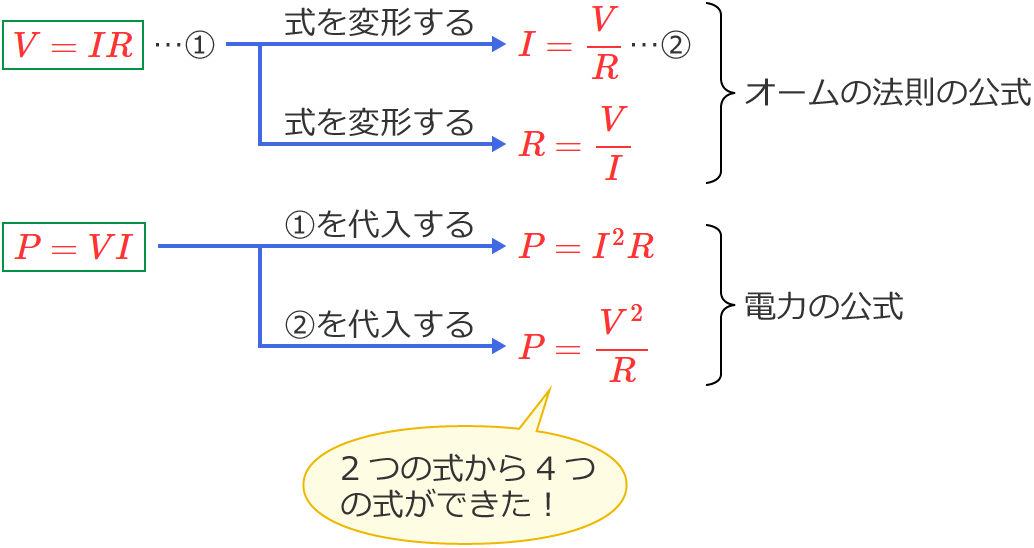
オームの法則の公式と電力の公式

6つ丸暗記するか…、計算するか…。

抵抗を示す式を求める計算問題（過去問題）と解き方

抵抗 $R$［$\Omega$］に電圧 $V$［$\mathrm{V}$］を加えると、電流 $I$［$\mathrm{A}$］が流れ、$P$［$\mathrm{W}$］の電力が消費される場合、抵抗 $R$［$\Omega$］を示す式として、誤っているものは。

イ．$\dfrac{PI}{V}$ロ．$\dfrac{P}{I^2}$ハ．$\dfrac{V^2}{P}$ニ．$\dfrac{V}{I}$

出題：令和3年度上期午前問2

解き方

この問題は、抵抗を $R$ 、電圧を $V$ 、電流を $I$ 、電力を $P$ とした場合に、選択肢それぞれの式が抵抗 $R$ になるかどうか考えればいい問題です。

この問題を、先ほどおぼえた6つの公式を使って考えてみましょう。

オームの法則と電力の6つの公式
オームの法則の公式	$V=IR$
	$I=\dfrac{V}{R}$
	$R=\dfrac{V}{I}$
電力の公式	$P=VI$
	$P=I^2R$
	$P=\dfrac{V^2}{R}$

「イ」は飛ばして、「ロ」から考えてみます。（「イ」を飛ばすってことは…。）

「ロ」の式は、$P$ と $I^2$ がある式ですね。電力の公式に $P$ と $I^2$ を含んでいる式（ $P=I^2R$ ）があるので、この式を使うと「ロ」の式が抵抗 $R$ になるかどうか分かりそうです。計算してみましょう。

$P=I^2R$　（$P$ と $I^2$ を含んでいる電力の公式）

$\therefore \dfrac{P}{I^2} =R$　（両辺を $I^2$ で割った）

なので、「ロ」の式（ $\dfrac{P}{I^2}$ ）は抵抗 $R$ になります！

「ハ」の式は、$P$ と $V^2$ がある式ですね。電力の公式に $P$ と $V^2$ を含んでいる式（ $P=\dfrac{V^2}{R}$ ）があるので、この式を使うと「ハ」の式が抵抗 $R$ になるかどうか分かりそうです。計算してみましょう。

$P=\dfrac{V^2}{R}$　（$P$ と $V^2$ を含んでいる電力の公式）

$P\times R=V^2$　（両辺に $R$ をかけた）

$R=\dfrac{V^2}{P}$　（両辺を $P$ で割った）

$\therefore \dfrac{V^2}{P} =R$

なので、「ハ」の式（ $\dfrac{V^2}{P}$ ）は抵抗 $R$ になります！

「ニ」の式は、$V$ と $I$ がある式ですね。オームの法則の公式に $V$ と $I$ を含んでいる式（ $R=\dfrac{V}{I}$ ）があるので、この式を使うと「ニ」の式が抵抗 $R$ になるかどうか分かりそうです。計算してみましょう…。ん？、これは計算する必要もなく、そのまんまでした。

$\therefore \dfrac{V}{I} =R$

なので、「ニ」の式（ $\dfrac{V}{I}$ ）は抵抗 $R$ になります！

以上より、「ロ」「ハ」「ニ」は抵抗 $R$ を示す式になっているので、正解（誤っているもの）は「イ」になります。

ちなみに、「イ」は計算せずに飛ばして解説をしましたが（「イ」は抵抗 $R$ にならないのね）、この「イ」は何になるでしょうか？

ちょっと計算してみると…、

$\dfrac{PI}{V}$　（「イ」の式）

$=\dfrac{\color{#ff3333}{VI}\times I}{V}$　（$P=VI$ より、$P$ に $VI$ を代入した）

$=\dfrac{VI^2}{V} =I^2$

となって、「イ」の $\dfrac{PI}{V}$ の式は電流の2乗（$I^2$）になります。

電流の2乗が抵抗になるかといえば、もちろんならないので、「イ」は抵抗 $R$ を示す式ではないですよ！ということになります。

ここの解説では「イ」を飛ばして「ロ」から計算しましたが、「イ」の計算をしただけでも答えが分かってしまうんですね。

解答：イ

問題1の別解①（ $\boldsymbol{V}$ に $\boldsymbol{IR}$ 、$\boldsymbol{P}$ に $\boldsymbol{I^2R}$ を代入する方法）

選択肢の式と公式を一つ一つ照らし合わせて考えるのは、なんだかめんどくさい感じがするなーという方は、次のような解き方をしてもいいと思います。

この問題は、選択肢それぞれの式が抵抗 $R$ になるかどうか？という問題なので、選択肢それぞれの式をどうにかして$\boldsymbol{R}$ だけにできないか考えてみればいいです。

選択肢の式に使われている文字は「 $V$ 」「 $I$ 」「 $P$ 」の3つですよね。（VIP（ビップ）だなー。）

この3つの文字を「 $R$ 」と「何か」の2つの文字だけ（またはどちらか1つの文字）で表わすことができれば、抵抗 $R$ を示す式の場合は、「何か」の文字は消えて最終的に「 $R$ 」だけになるんじゃないかと。

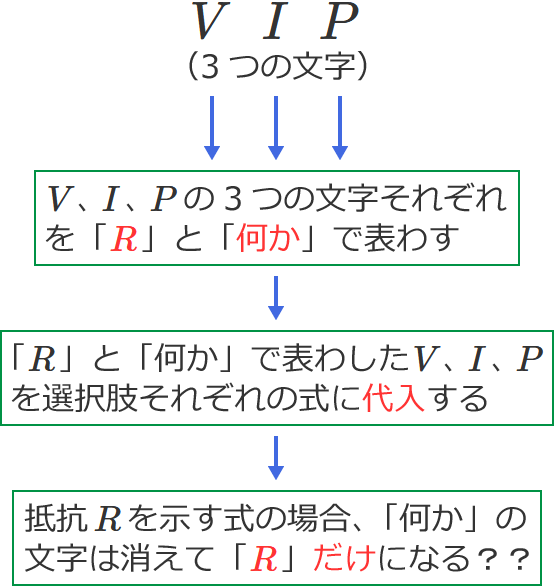
抵抗Rだけにする解き方

例えば、3つの文字「 $V$ 」「 $I$ 」「 $P$ 」のうちの「 $V$ 」は、オームの法則の公式に $V=IR$ という式があるので、「 $V$ 」は「 $R$ 」と「 $I$ 」で表わすことができます。

また、3つの文字「 $V$ 」「 $I$ 」「 $P$ 」のうちの「 $P$ 」は、電力の公式に $P=I^2R$ という式があるので、「 $P$ 」は「 $R$ 」と「 $I$ 」で表わすことができます。

なので、「 $I$ 」はそのまま $I$ とすれば、3つの文字「 $V$ 」「 $I$ 」「 $P$ 」は「 $R$ 」と「 $I$ 」だけで表わすことができます。

つまり、こうするとよさそうだ！

$V$ は $V=IR$ より、$IR$ に置き換える。
$I$ はそのまま $I$ とする。
$P$ は $P=I^2R$ より、$I^2R$ に置き換える。

では、選択肢それぞれの式の $V$ には $IR$ 、$P$ には $I^2R$ を代入してみましょう。（ $I$ はそのまま $I$ です。）

イ．$\dfrac{PI}{V} =\dfrac{\color{#ff3333}{I^2R}\times I}{\color{#ff3333}{IR}}$　（$V$ に $IR$ 、$P$ に $I^2R$ を代入した）

$=\dfrac{I^3R}{IR}=I^2$

「イ」は $I^2$ になりました。

ロ．$\dfrac{P}{I^2} =\dfrac{\color{#ff3333}{I^2R}}{I^2}$　（$P$ に $I^2R$ を代入した）

$=R$

「ロ」は $R$ になりました！

ハ．$\dfrac{V^2}{P} =\dfrac{\left( \color{#ff3333}{IR}\right)^2}{\color{#ff3333}{I^2R}}$　（$V$ に $IR$ 、$P$ に $I^2R$ を代入した）

$=\dfrac{I^2R^2}{I^2R}=R$

「ハ」は $R$ になりました！

ニ．$\dfrac{V}{I} =\dfrac{\color{#ff3333}{IR}}{I}$　（$V$ に $IR$ を代入した）

$=R$

「ニ」は $R$ になりました！

以上より、「ロ」「ハ」「ニ」は抵抗 $R$ を示す式になっていて、「イ」は抵抗 $R$ を示す式になっていないことが分かりました。（「イ」が正解（誤っているもの））

文字を使った式の計算が苦手ではない方の場合は、この解き方の方がやりやすいかもです。

ちなみに、ここでやっている計算方法を簡単に説明すると、

$V=IR$ より、$V$ に $IR$ を代入
$P=I^2R$ より、$P$ に $I^2R$ を代入

としているだけです。（長々と書いていますが、これだけなんです…。）

解答：イ

問題1の別解②（ $\boldsymbol{I}$ に $\boldsymbol{V/R}$ 、$\boldsymbol{P}$ に $\boldsymbol{V^2/R}$ を代入する方法）

別解②は別解①と同じような解き方ですが、オームの法則の公式の $I=\dfrac{V}{R}$ と電力の公式の $P=\dfrac{V^2}{R}$ を使って、選択肢それぞれの式の $I$ に $\dfrac{V}{R}$ 、$P$ に $\dfrac{V^2}{R}$ を代入する方法です。

この計算方法の場合、選択肢それぞれの式を「 $R$ 」と「 $V$ 」だけの式にすることができます。

では、選択肢それぞれの式の $I$ には $\dfrac{V}{R}$ 、$P$ には $\dfrac{V^2}{R}$ を代入してみましょう。（ $V$ はそのまま $V$ です。）

イ．$\dfrac{PI}{V} =\dfrac{\color{#ff3333}{\dfrac{V^2}{R}}\times\color{#ff3333}{\dfrac{V}{R}}}{V}$　（$I$ に $\dfrac{V}{R}$ 、$P$ に $\dfrac{V^2}{R}$ を代入した）

$=\dfrac{V^2}{R}\times\dfrac{V}{R}\times\dfrac{1}{V} =\dfrac{V^3}{R^2V}$ $=\dfrac{V^2}{R^2} =\left( \dfrac{V}{R}\right)^2$

「イ」は $\left( \dfrac{V}{R}\right)^2$ になりました。

オームの法則の公式より $\dfrac{V}{R}$ は電流 $I$ になるので、上式の $\left( \dfrac{V}{R}\right)^2$ は $I^2$（電流の2乗）になります。

ロ．$\dfrac{P}{I^2} =\dfrac{\color{#ff3333}{\dfrac{V^2}{R}}}{\left(\color{#ff3333}{\dfrac{V}{R}}\right)^2}$　（$I$ に $\dfrac{V}{R}$ 、$P$ に $\dfrac{V^2}{R}$ を代入した）

$=\dfrac{\dfrac{V^2}{R}}{\dfrac{V^2}{R^2}} =\dfrac{V^2}{R}\times \dfrac{R^2}{V^2} =\dfrac{R^2V^2}{RV^2}$ $=R$

「ロ」は $R$ になりました！

ハ．$\dfrac{V^2}{P} =\dfrac{V^2}{\color{#ff3333}{\dfrac{V^2}{R}}}$　（$P$ に $\dfrac{V^2}{R}$ を代入した）

$=V^2\times \dfrac{R}{V^2} =\dfrac{V^2R}{V^2} =R$

「ハ」は $R$ になりました！

ニ．$\dfrac{V}{I} =\dfrac{V}{\color{#ff3333}{\dfrac{V}{R}}}$　（$I$ に $\dfrac{V}{R}$ を代入した）

$=V\times \dfrac{R}{V} =\dfrac{VR}{V} =R$

「ニ」は $R$ になりました！

別解②の場合は分数が多くなるので、別解①よりもちょっとだけ計算が大変になりますね。

解答：イ

抵抗を示す式を求める計算問題の解き方の解説は以上になりますが、抵抗を示す式を求める計算問題を解くためには、電気の基本公式（オームの法則の公式、電力の公式）の知識が必要になります。

このページに掲載しているオームの法則の公式と電力の公式は、第二種電気工事士学科試験で出題されている他の計算問題を解くときにもよく使う基本公式ですので、必ずおぼえておくようにしましょう。基本は大事！

第二種電気工事士学科試験の計算問題の解き方のまとめページはこちら
⇒ 第二種電気工事士学科試験の計算問題の解き方

このページに掲載の問題（過去問題）は、（一財）電気技術者試験センターが作成した第二種電気工事士学科試験の問題です。なお、多少の違いがあっても問題としては同じと考えられる問題については、同じ問題として記載しています。

第二種電気工事士（学科試験対策）のＴＯＰ　←BACK

NEXT→　導線の電気抵抗を表わす式を求める計算問題の解き方

抵抗を示す式を求める計算問題の解き方　関連ページ

導線の電気抵抗を表わす式を求める計算問題の解き方: 第二種電気工事士学科試験で出題されている「導線の電気抵抗を表わす式を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
導線の抵抗率を表わす式を求める計算問題の解き方: 第二種電気工事士学科試験で出題されている「導線の抵抗率を表わす式を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
抵抗値が最も近い同材質の銅導線を求める計算問題の解き方: 第二種電気工事士学科試験で出題されている「抵抗値が最も近い同材質の銅導線を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
2本の銅線の抵抗の比を求める計算問題の解き方: 第二種電気工事士学科試験で出題されている「2本の銅線の抵抗の比を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。

第二種電気工事士｜学科試験対策｜抵抗を示す式を求める計算問題の解き方