スポンサーリンク
抵抗値が最も近い同材質の銅導線を求める計算問題の解き方
※ページ内にPR・広告が含まれる場合があります。
第二種電気工事士学科試験の抵抗値が最も近い同材質の銅導線を求める計算問題の解き方について解説しています。
第二種電気工事士学科試験を受験する方の中には、
計算問題が苦手!とか、
計算問題はもう捨てちゃいました!(捨てないで〜)
という方もいるかもしれませんが、第二種電気工事士学科試験で出題されている計算問題のほとんどは、
- 過去に出題された計算問題とまったく同じ問題
- 過去に出題された計算問題の数値を変えただけの問題
- ちょっとだけ何か(?)を変えた類似問題
で、出題項目ごとに過去問題を見てみると、問題の出題パターンもほぼ同じです。
ですので、計算問題が苦手な方でも、出題項目ごとにおぼえることをおぼえて解き方のパターンに慣れてしまえば、計算問題でも点数をとれるようになります。
このページでは、過去に試験で出題された過去問題を使って抵抗値が最も近い同材質の銅導線を求める計算問題の解き方について解説していますので、このページを読んで抵抗値が最も近い同材質の銅導線を求める計算問題を解けるようになりましょう。
計算問題も解けるようになると、合格がぐぐぐーん!と近づきますよ!
問題には過去問題を使っていますので、過去問題の勉強にもなると思います。
スポンサーリンク
抵抗値が最も近い同材質の銅導線を求める計算問題を解くための基礎知識
まず初めに、抵抗値が最も近い同材質の銅導線を求める計算問題を解くためにおぼえておかなければならないことをおぼえてしまいましょう。
抵抗値が最も近い同材質の銅導線を求める計算問題を解けるようになるためにおぼえておかなければならないのは、次の2つの電線の抵抗の公式です。
- 電線の太さが断面積の電線の抵抗の公式
- 電線の太さが直径の電線の抵抗の公式
この2つの公式をおぼえておけば、あとはこの公式のどちらかに問題で与えられた値(条件)を当てはめて各銅導線の抵抗値を求め、問題文に書かれている銅導線と抵抗値が最も近い銅導線を選ぶだけです。
銅導線の太さが断面積の場合は「電線の太さが断面積の電線の抵抗の公式」、銅導線の太さが直径の場合は「電線の太さが直径の電線の抵抗の公式」を使います。
電線の太さが断面積の電線の抵抗の公式
電線の太さが断面積の電線の抵抗の公式は次のような公式で、この公式の電線の太さは断面積で与えられます。
電線の太さが断面積の電線の抵抗の公式:$R=\rho\dfrac{L}{S}$ …①
①式の $R$ は電線の抵抗[$\Omega$]、$\rho$ は電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$]、$L$ は電線の長さ[$\mathrm{m}$]、$S$ は電線の断面積[$\mathrm{m^2}$]を表わし、①式は、電線の抵抗率 $\rho$ 、電線の長さ $L$ 、電線の断面積 $S$ が分かれば、電線の抵抗 $R$ を求めることができますよ、という式です。
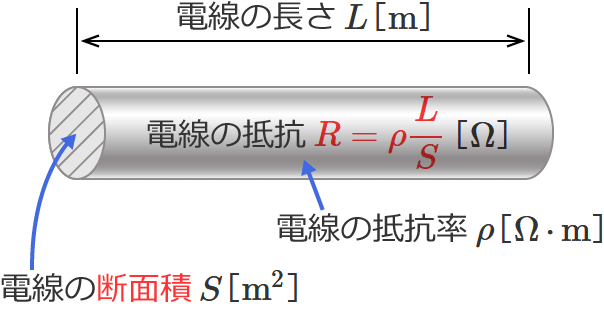
ここで、①式を見てみると$\boldsymbol{\rho}$(抵抗率)というものがありますが、この抵抗率 $\rho$ は、電線の材料(材質)が同じ場合は、電線の長さや太さが変わっても値(抵抗率 $\rho$ の値)は変わりません。
抵抗率 $\rho$[$\Omega\,\cdotp\mathrm{m}$]は、電線の長さを $1\,\mathrm{m}$(単位長さ)、電線の断面積を $1\,\mathrm{m^2}$(単位断面積)としたときの電線の抵抗値を示します。
$R=\rho\dfrac{L}{S}$ $R=\rho\dfrac{1\left[ \mathrm{m}\right]}{1\left[ \mathrm{m^2}\right]}$ $\therefore R=\rho$
なので、電線の材料(材質)が同じであれば、電線の長さや太さが変わっても抵抗率の値は変わりません。(抵抗率は、電線の長さや太さには依存しないってことですね。)
例えば、「銅でできている電線」と「アルミニウムでできている電線」があるとすると、この2本の電線は異なる材料でできているので、この2本の電線の抵抗率は異なる値になります。
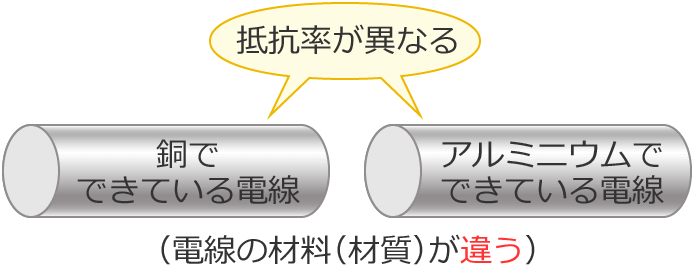
また、「銅でできている電線」と「銅でできている電線」(同じ材質の電線)があるとすると、この2本の電線は同じ材料でできているので、この2本の電線の抵抗率は同じ値になります。(電線の長さや太さが変わっても、抵抗率の値は変わりません。)
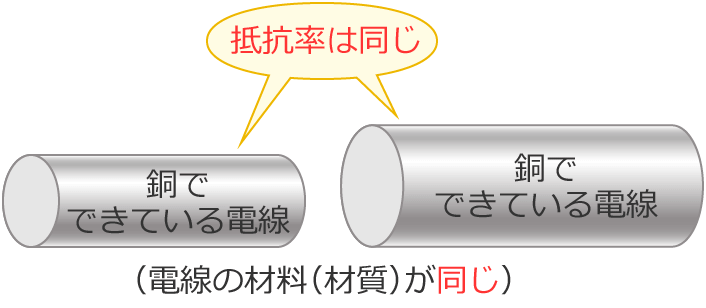
抵抗値が最も近い同材質の銅導線を求める計算問題の問題文には、よく同材質の銅導線と書いてあるんですけど、これは、
同材質(の銅導線) ⇒ 抵抗率が同じ(銅導線)
ということになります。問題文に同材質と書いてあったら抵抗率は同じとおぼえておきましょう。
電線の太さが断面積の電線の抵抗の公式については、ここでは「①式」と「電線の材料(材質)が同じ場合は、抵抗率は同じ値になる」をおぼえておけばいいのですが、ここで、ちょっとだけ注意することがあります。(ちょっとじゃないけど…。)
そ、それは、単位です!
①式中の $S$ は電線の断面積を表わしますが、この $S$ の単位は$\boldsymbol{\mathrm{m^2}}$(平方メートル)です。
なので、問題に書かれている電線の断面積の単位が「 $\mathrm{mm^2}$ 」(平方ミリメートル)だったら、その電線の断面積を「 $\mathrm{mm^2}$ 」(平方ミリメートル)から「 $\mathrm{m^2}$ 」(平方メートル)に直して①式の公式に代入しなければなりません。(換算が必要ってことです。)
$\mathrm{mm^2}$(平方ミリメートル)を $\mathrm{m^2}$(平方メートル)に直す(換算する)ときは、$\mathrm{mm^2}$(平方ミリメートル)の値に $10^{-6}$ をかけます。例えば、$1\,000\,000\,\mathrm{mm^2}$(百万平方ミリメートル) …② を平方メートルに直すときは、②の値に $10^{-6}$ をかけます。
$1\,000\,000$[$\mathrm{mm^2}$]$\times\color{#ff3333}{10^{-6}}$ ⇒ $1$[$\mathrm{m^2}$] ($1\,000\,000\,\mathrm{mm^2}$ は $1\,\mathrm{m^2}$ になる)
断面積が $8\,\mathrm{mm^2}$ だったら、これも同じようにして、$8$ に $10^{-6}$ をかけます。
$8$[$\mathrm{mm^2}$]$\times\color{#ff3333}{10^{-6}}$ ⇒ $8\times 10^{-6}$[$\mathrm{m^2}$] ($8\,\mathrm{mm^2}$ は $8\times 10^{-6}\,\mathrm{m^2}$ になる)
もし、$\mathrm{mm^2}$ を $\mathrm{m^2}$ に直すときに $10$ の何乗だったか忘れてしまった場合は、$1$ 平方メートルは何平方ミリメートルになるか考えてみると分かります。
- $1\,\mathrm{cm}$ は $10\,\mathrm{mm}$
- $10\,\mathrm{cm}$ は $100\,\mathrm{mm}$
- $100\,\mathrm{cm}$( $1\,\mathrm{m}$ )は $1\,000\,\mathrm{mm}$
ということは、
- $1\,\mathrm{m^2}$ は $1\,000\,\mathrm{mm}\times1\,000\,\mathrm{mm}$ で、$1\,000\,000\,\mathrm{mm^2}$ ($\mathrm{m^2}$ と $\mathrm{mm^2}$ は $1:1\,000\,000$ )
となるから、$\mathrm{mm^2}$ を $\mathrm{m^2}$ に直すときは $1\,000\,000$( $=10^6$ )で割る。ということは、$10^{-6}$ をかけるんだー!てな感じで。
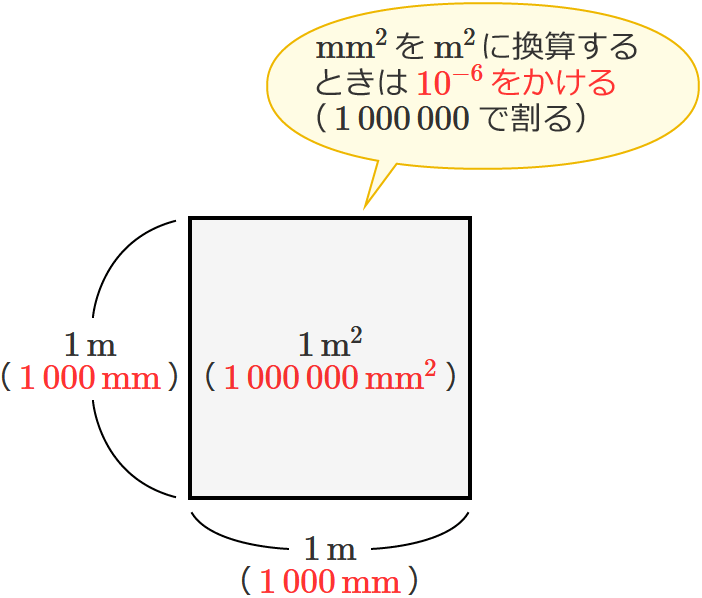
$\dfrac{1}{1\,000\,000} =\dfrac{1}{10^6} =10^{-6}$ になります。なので、$1\,000\,000$ で割るというのは、$10^{-6}$ をかけるのと同じです。
この $\mathrm{mm^2}$ から $\mathrm{m^2}$ への換算は、他の抵抗の計算問題を解くときにも使うのでおぼえておきましょう。
電線の太さが直径の電線の抵抗の公式
電線の太さが直径の電線の抵抗の公式は次のような公式で、この公式の電線の太さは直径で与えられます。
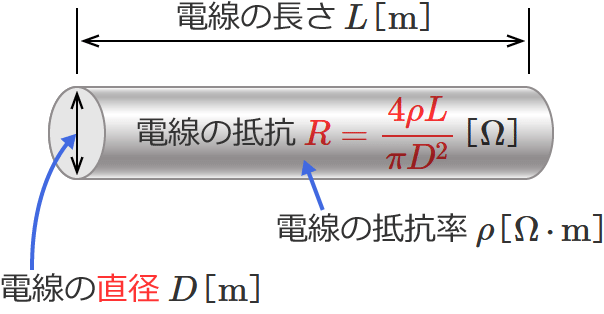
電線の太さが直径の電線の抵抗の公式:$R=\dfrac{4\rho L}{\pi D^2}$ …③
③式の $R$ は電線の抵抗[$\Omega$]、$\rho$ は電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$]、$L$ は電線の長さ[$\mathrm{m}$]、$D$ は電線の直径[$\mathrm{m}$]を表わし、③式は、電線の抵抗率 $\rho$ 、電線の長さ $L$ 、電線の直径 $D$ が分かれば、電線の抵抗 $R$ を求めることができますよ、という式です。
③式中の $\pi$ は円周率( $\pi\fallingdotseq 3.14$ )で、円の面積とかを求めるときによく使うやつですね。円の面積 $=\pi\times r^2$( $\text{円周率}\times\text{半径}^2$ )みたいなね。
電線の太さが直径の電線の抵抗の公式については、ここでは「③式」と先ほど①式のところで解説した「電線の材料(材質)が同じ場合は、抵抗率は同じ値になる」をおぼえておけばいいのですが、ここでも、ちょっとだけ注意することがあります。(これも、ちょっとじゃないけど…。)
そ、それは、ここでも単位です!
③式中の $D$ は電線の直径を表わしますが、この $D$ の単位は$\boldsymbol{\mathrm{m}}$(メートル)です。
なので、問題に書かれている電線の直径の単位が「 $\mathrm{mm}$ 」(ミリメートル)だったら、その電線の直径を「 $\mathrm{mm}$ 」(ミリメートル)から「 $\mathrm{m}$ 」(メートル)に直して③式の公式に代入しなければなりません。(換算が必要ってことです。)
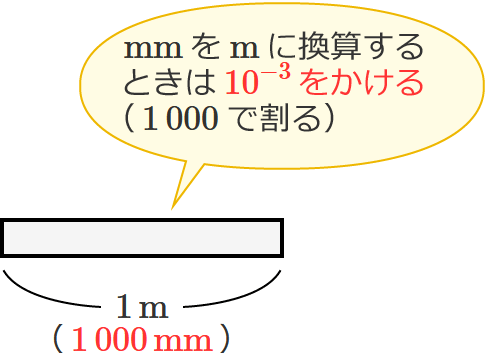
$\mathrm{mm}$(ミリメートル)を $\mathrm{m}$(メートル)に直す(換算する)ときは、$\mathrm{mm}$(ミリメートル)の値に $10^{-3}$ をかけます。例えば、$1\,000\,\mathrm{mm}$(千ミリメートル) …④ をメートルに直すときは、④の値に $10^{-3}$ をかけます。
$1\,000$[$\mathrm{mm}$]$\times\color{#ff3333}{10^{-3}}$ ⇒ $1$[$\mathrm{m}$] ($1\,000\,\mathrm{mm}$ は $1\,\mathrm{m}$ になる)
直径が $2.6\,\mathrm{mm}$ だったら、これも同じようにして、$2.6$ に $10^{-3}$ をかけます。
$2.6$[$\mathrm{mm}$]$\times\color{#ff3333}{10^{-3}}$ ⇒ $2.6\times 10^{-3}$[$\mathrm{m}$] ($2.6\,\mathrm{mm}$ は $2.6\times 10^{-3}\,\mathrm{m}$ になる)
もし、$\mathrm{mm}$ を $\mathrm{m}$ に直すときに $10$ の何乗だったか忘れてしまった場合は、次のように $1$ センチは何ミリで…、と書いてみると分かります。
- $1\,\mathrm{cm}$ は $10\,\mathrm{mm}$
- $10\,\mathrm{cm}$ は $100\,\mathrm{mm}$
- $100\,\mathrm{cm}$( $1\,\mathrm{m}$ )は $1\,000\,\mathrm{mm}$ ($\mathrm{m}$ と $\mathrm{mm}$ は $1:1\,000$ )
となるから、$\mathrm{mm}$ を $\mathrm{m}$ に直すときは $1\,000$( $=10^3$ )で割る。ということは、$10^{-3}$ をかけるんだー!てな感じで。
$\dfrac{1}{1\,000} =\dfrac{1}{10^3} =10^{-3}$ になります。なので、$1\,000$ で割るというのは、$10^{-3}$ をかけるのと同じです。
この $\mathrm{mm}$ から $\mathrm{m}$ への換算は、他の抵抗の計算問題を解くときにも使うので、先ほどの $\mathrm{mm^2}$ から $\mathrm{m^2}$ への換算といっしょにおぼえておきましょう。
- $\mathrm{mm^2}$ から $\mathrm{m^2}$ へ換算するときは、$10^{-6}$ をかける
- $\mathrm{mm}$ から $\mathrm{m}$ へ換算するときは、$10^{-3}$ をかける
以上の「電線の太さが断面積の電線の抵抗の公式」と「電線の太さが直径の電線の抵抗の公式」をおぼえたら、抵抗値が最も近い同材質の銅導線を求める計算問題を解くための基礎知識はOKです!
では、過去に第二種電気工事士学科試験で出題された過去問題を解いてみましょう!
断面積の公式から直径の公式を導出できる!
次のようにすると、「電線の太さが断面積の電線の抵抗の公式」から「電線の太さが直径の電線の抵抗の公式」を導くことができます。
$R=\rho\dfrac{L}{S}$ …⑤ (電線の太さが断面積の電線の抵抗の公式)
この公式の「 $S$ 」は断面積なので、電線の直径を $D$ とした場合、断面積 $S$ は、
$S=\pi\times\left( \dfrac{D}{2}\right)^2$ …⑥
$=\pi\times\dfrac{D^2}{4} =\dfrac{\pi D^2}{4}$
$\therefore S=\dfrac{\pi D^2}{4}$ …⑦ と表わせます。
⑥では、円の面積の公式( $\text{円周率}\pi\times\text{半径}^2$ )を使っています。$D$ は直径なので、半径は $\dfrac{D}{2}$ になります。
この⑦を⑤式に代入します。
$R=\rho\dfrac{L}{S}$ (⑤式)
$=\rho\dfrac{L}{\color{#ff3333}{\dfrac{\pi D^2}{4}}}$ (⑦を⑤式に代入した)
$=\dfrac{\rho L}{\dfrac{\pi D^2}{4}} =\rho L\times\dfrac{4}{\pi D^2} =\dfrac{4\rho L}{\pi D^2}$
$\therefore \color{#ff3333}{R=\dfrac{4\rho L}{\pi D^2}}$ (電線の太さが直径の電線の抵抗の公式)
導出できた!
以上のように円の面積の公式を使うと、「電線の太さが断面積の電線の抵抗の公式」から「電線の太さが直径の電線の抵抗の公式」を導くことができるので、「電線の太さが直径の電線の抵抗の公式」を忘れてしまったときは計算してみるといいと思います。

2つの公式どっちも忘れてしまったときはどうしましょう…。
スポンサーリンク
スポンサーリンク
抵抗値が最も近い同材質の銅導線を求める計算問題(過去問題)と解き方
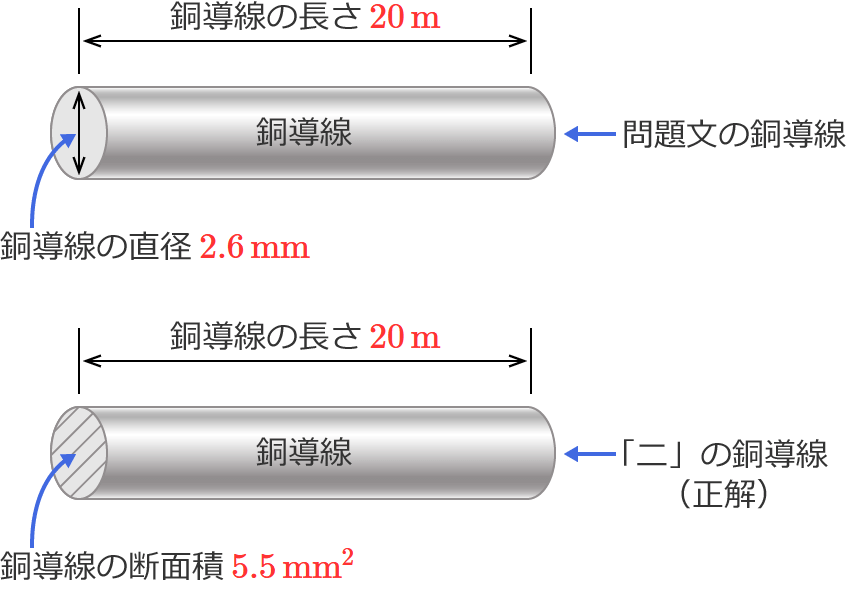
直径 $2.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$ の銅導線と抵抗値が最も近い同材質の銅導線は。
イ.断面積 $8\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$
ロ.断面積 $8\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$
ハ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$
ニ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$
出題:令和3年度上期午後問2
解き方
この問題は、問題文に書かれている銅導線と抵抗値が最も近い銅導線を選択肢の中から選ぶ問題なので、「問題文の銅導線の抵抗」(1つ)と「選択肢の銅導線の抵抗」(4つ)を求めてしまえば正解が分かります。
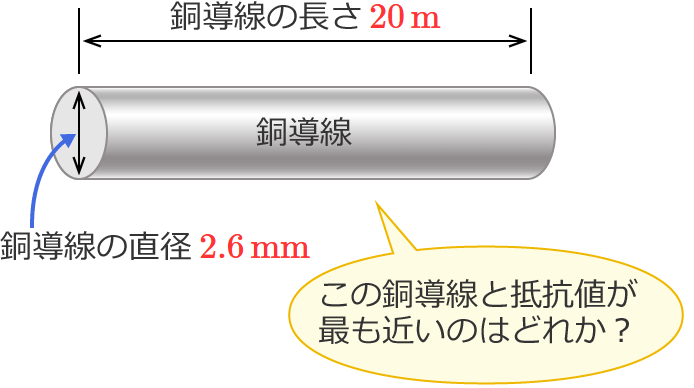
銅導線の抵抗は、先ほどおぼえた電線の抵抗の公式を使えば求められるのですが、問題を読んでみると、各銅導線の長さと太さ(直径または断面積)は書いてあるので分かりますが、抵抗率は書いてないので分かりません。
ですが、問題文に同材質の銅導線と書いてあるので、「問題文の銅導線の抵抗率と選択肢の各銅導線の抵抗率は同じになる」ということが分かります。(電線の材質が同じだったら、抵抗率も同じになるのでした。)
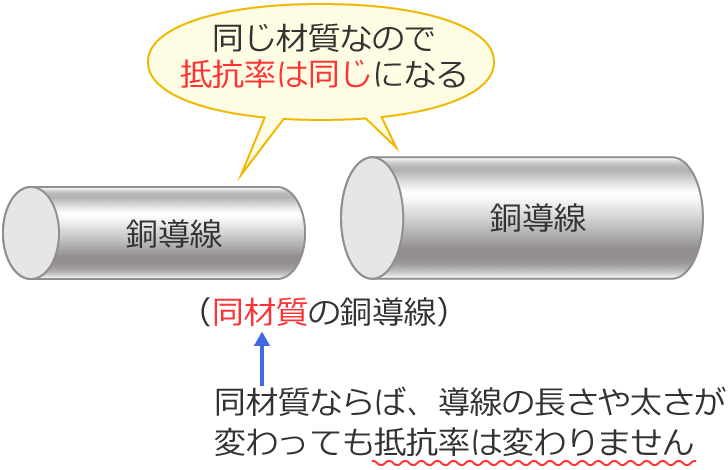
なので、抵抗率の値は分かりませんが、どの銅導線も同じ抵抗率になるので、銅導線の抵抗率をすべて $\rho$[$\Omega\,\cdotp\mathrm{m}$]として各銅導線の抵抗を求めます。
もちろん、求めた抵抗には $\rho$ が含まれてしまいますが、この問題は「抵抗値が最も近い銅導線を選ぶ問題」なので、$\rho$ があっても大丈夫!です。
では、抵抗率をすべて $\rho$[$\Omega\,\cdotp\mathrm{m}$]として、それぞれの銅導線の抵抗を求めてみましょう。
各銅導線の抵抗を求めるときは、銅導線の太さが断面積の場合は「電線の太さが断面積の電線の抵抗の公式」(次の①式)、銅導線の太さが直径の場合は「電線の太さが直径の電線の抵抗の公式」(次の②式)を使います。
$R=\rho\dfrac{L}{S}$ …① (電線の太さが断面積の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $S$:電線の断面積[$\mathrm{m^2}$]
$R=\dfrac{4\rho L}{\pi D^2}$ …② (電線の太さが直径の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $D$:電線の直径[$\mathrm{m}$]
問題文の銅導線の抵抗
問題文の銅導線は、直径 $2.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{問題文}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{20}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{2.6\times 10^{-3}}\right)^2}$ …③ (問題文の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{80\rho}{3.14\times 2.6^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{80\rho}{21.2\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{80\rho}{21.2}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 3.77\rho\times 10^6 =3.77\times 10^6\rho$
$\therefore R_{\,\text{問題文}} =\color{#ff3333}{3.77\times 10^6\rho}$
③の直径 $D$ には、直径 $2.6$[$\mathrm{mm}$]をメートルに換算した $2.6\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「イ」の銅導線の抵抗
「イ」の銅導線は、断面積 $8\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{イ}} =\rho\times\dfrac{\color{#ff3333}{40}}{\color{#ff3333}{8\times 10^{-6}}}$ …④ (「イ」の値を代入した)
$=\dfrac{40\rho}{8\times 10^{-6}}$
$=\dfrac{40\rho}{8}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$=5\rho\times 10^6 =5\times 10^6\rho$
$\therefore R_{\,\text{イ}} =5\times 10^6\rho$
④の断面積 $S$ には、断面積 $8$[$\mathrm{mm^2}$]を平方メートルに換算した $8\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ロ」の銅導線の抵抗
「ロ」の銅導線は、断面積 $8\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ロ}} =\rho\times\dfrac{\color{#ff3333}{20}}{\color{#ff3333}{8\times 10^{-6}}}$ …⑤ (「ロ」の値を代入した)
$=\dfrac{20\rho}{8\times 10^{-6}}$
$=\dfrac{20\rho}{8}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$=2.5\rho\times 10^6 =2.5\times 10^6\rho$
$\therefore R_{\,\text{ロ}} =2.5\times 10^6\rho$
⑤の断面積 $S$ には、断面積 $8$[$\mathrm{mm^2}$]を平方メートルに換算した $8\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ハ」の銅導線の抵抗
「ハ」の銅導線は、断面積 $5.5\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ハ}} =\rho\times\dfrac{\color{#ff3333}{40}}{\color{#ff3333}{5.5\times 10^{-6}}}$ …⑥ (「ハ」の値を代入した)
$=\dfrac{40\rho}{5.5\times 10^{-6}}$
$=\dfrac{40\rho}{5.5}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 7.27\rho\times 10^6 =7.27\times 10^6\rho$
$\therefore R_{\,\text{ハ}} =7.27\times 10^6\rho$
⑥の断面積 $S$ には、断面積 $5.5$[$\mathrm{mm^2}$]を平方メートルに換算した $5.5\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ニ」の銅導線の抵抗
「ニ」の銅導線は、断面積 $5.5\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ニ}} =\rho\times\dfrac{\color{#ff3333}{20}}{\color{#ff3333}{5.5\times 10^{-6}}}$ …⑦ (「ニ」の値を代入した)
$=\dfrac{20\rho}{5.5\times 10^{-6}}$
$=\dfrac{20\rho}{5.5}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 3.64\rho\times 10^6 =3.64\times 10^6\rho$
$\therefore R_{\,\text{ニ}} =\color{#ff3333}{3.64\times 10^6\rho}$
⑦の断面積 $S$ には、断面積 $5.5$[$\mathrm{mm^2}$]を平方メートルに換算した $5.5\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
以上より、問題文の銅導線と抵抗値が最も近いものは「ニ」になります。
ちなみに、ここでやっている計算方法を簡単にまとめると、
- 銅導線の太さが直径の場合は、直径の公式に各値を代入して銅導線の抵抗を求める
- 銅導線の太さが断面積の場合は、断面積の公式に各値を代入して銅導線の抵抗を求める
- ただし、抵抗率は $\rho$ とし、問題の単位は公式の単位に合わせる
となります。
解答:ニ
問題1の別解①(問題の銅導線の直径を断面積に換算して比較する方法)
この問題は、問題文の銅導線の直径を断面積に換算して、選択肢の銅導線と比較することでも正解を見つけることができます。
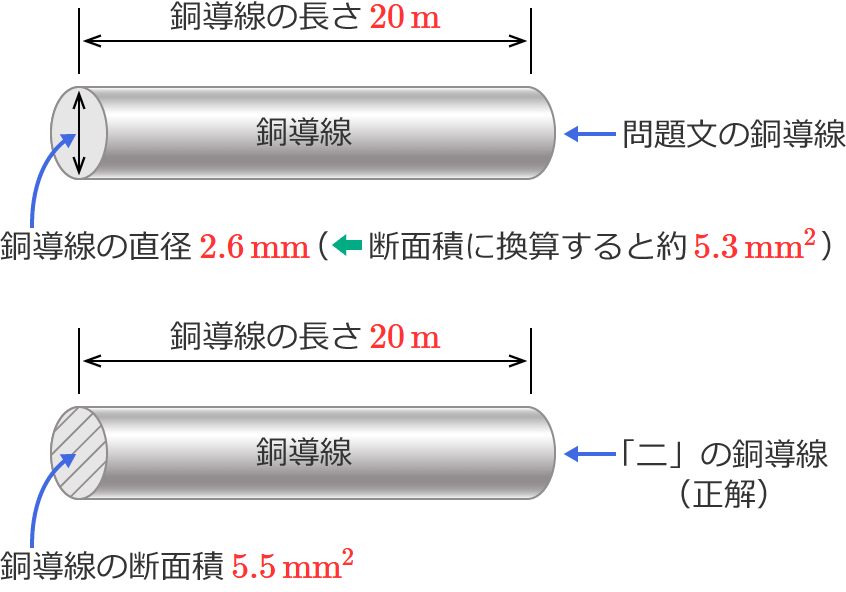
問題文の銅導線の直径は $2.6\,\mathrm{mm}$ なので、これを断面積[$\mathrm{mm^2}$]に換算してみると次のようになります。
問題文の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{2.6}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 1.3^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 1.69 \fallingdotseq 5.3$
$\therefore$ 問題文の銅導線の断面積 $\fallingdotseq \color{#ff3333}{5.3\,\mathrm{mm^2}}$
なので、直径を断面積に換算した問題文の銅導線は、断面積約 $\boldsymbol{5.3\,\mathrm{mm^2}}$ 、長さ $\boldsymbol{20\,\mathrm{m}}$になります。
これと抵抗値が最も近くなるのは選択肢のどの銅導線か、「イ」から見てみましょう。(ぱっとみ、「ニ」が正解っぽいけど…。)
イ.断面積 $8\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$ (「イ」の銅導線)
「イ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは2倍になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが2倍なら断面積も2倍くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「イ」の銅導線の断面積は $8\,\mathrm{mm^2}$ …、ちょっと足りないような…。
ちょっと分からないけど、違うっぽいですね。
次いってみましょう。
電線の抵抗は長さに比例し断面積に反比例する
電線の抵抗は、電線の抵抗の公式 $R=\rho\dfrac{L}{S}$ より、電線の長さ($L$)に比例し、電線の断面積($S$)に反比例します。なので、電線の長さが2倍になったら電線の抵抗 $R$ も2倍になるので、電線の抵抗 $R$ が同じになるためには、電線の断面積も2倍でなければなりません。

ロ.断面積 $8\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ (「ロ」の銅導線)
「ロ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは同じですね。
長さが同じなら断面積も同じくらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ロ」の銅導線の断面積は $8\,\mathrm{mm^2}$ …。
これは、違うっぽいですね。
次いってみましょう。
ハ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $40\,\mathrm{m}$ (「ハ」の銅導線)
「ハ」の銅導線は、問題文の銅導線とほぼ同じくらいの断面積で、長さは2倍になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが2倍なら断面積も2倍くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ハ」の銅導線の断面積は $5.5\,\mathrm{mm^2}$ …。
断面積がほぼ同じなので、これは違いますね。
次いってみましょう。
ニ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ (「ニ」の銅導線)
「ニ」の銅導線は、問題文の銅導線とほぼ同じくらいの断面積で、長さは同じですね。
長さが同じで、断面積がほぼ同じなので、正解はこれ!ですね。
以上より、問題文の銅導線と抵抗値が最も近いものは「ニ」になります。
別解①の解き方は一つ一つ値を求めていないのでちょっと不安(なんかモヤモヤする…)という方には、はじめの解き方をおすすめします。はじめの解き方の場合は、計算がそれなりにあるため少し大変ですが、きっちり答えが分かるのでスッキリ!すると思います。
解答:ニ
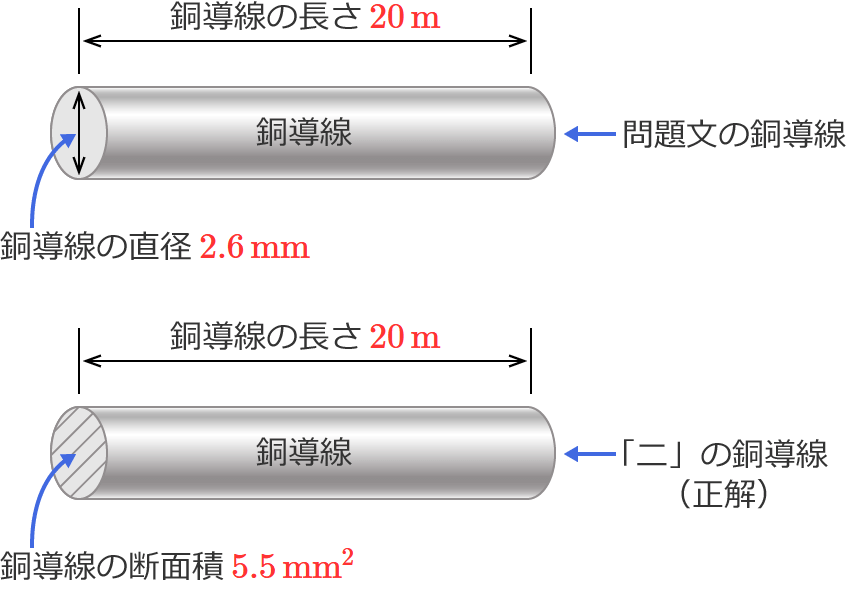
直径 $2.6$[$\mathrm{mm}$]、長さ $20$[$\mathrm{m}$]の銅導線と抵抗値が最も近い同材質の銅導線は。
イ.直径 $1.6$[$\mathrm{mm}$]、長さ $40$[$\mathrm{m}$]
ロ.断面積 $8$[$\mathrm{mm^2}$]、長さ $20$[$\mathrm{m}$]
ハ.直径 $3.2$[$\mathrm{mm}$]、長さ $10$[$\mathrm{m}$]
ニ.断面積 $5.5$[$\mathrm{mm^2}$]、長さ $20$[$\mathrm{m}$]
出題:平成26年度下期問3
解き方
問題2は問題1とほぼ同じ問題で、問題1と問題2の違いは、選択肢に直径の銅導線があるかないかくらいです。問題1と同じような解き方で解くことができますので、問題1の解き方と同じように解いてみます。

問題文に同材質の銅導線と書いてあるので、どの銅導線も抵抗率は同じです。なので、抵抗率をすべて $\rho$[$\Omega\,\cdotp\mathrm{m}$]として、それぞれの銅導線の抵抗を求めます。
各銅導線の抵抗を求めるときは、銅導線の太さが断面積の場合は「電線の太さが断面積の電線の抵抗の公式」(次の①式)、銅導線の太さが直径の場合は「電線の太さが直径の電線の抵抗の公式」(次の②式)を使います。
$R=\rho\dfrac{L}{S}$ …① (電線の太さが断面積の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $S$:電線の断面積[$\mathrm{m^2}$]
$R=\dfrac{4\rho L}{\pi D^2}$ …② (電線の太さが直径の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $D$:電線の直径[$\mathrm{m}$]
問題文の銅導線の抵抗
問題文の銅導線は、直径 $2.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{問題文}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{20}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{2.6\times 10^{-3}}\right)^2}$ …③ (問題文の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{80\rho}{3.14\times 2.6^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{80\rho}{21.2\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{80\rho}{21.2}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 3.77\rho\times 10^6 =3.77\times 10^6\rho$
$\therefore R_{\,\text{問題文}} =\color{#ff3333}{3.77\times 10^6\rho}$
③の直径 $D$ には、直径 $2.6$[$\mathrm{mm}$]をメートルに換算した $2.6\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「イ」の銅導線の抵抗
「イ」の銅導線は、直径 $1.6\,\mathrm{mm}$ 、長さ $40\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{イ}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{40}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{1.6\times 10^{-3}}\right)^2}$ …④ (「イ」の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{160\rho}{3.14\times 1.6^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{160\rho}{8.04\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{160\rho}{8.04}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 19.9\rho\times 10^6 =19.9\times 10^6\rho$
$\therefore R_{\,\text{イ}} =19.9\times 10^6\rho$
④の直径 $D$ には、直径 $1.6$[$\mathrm{mm}$]をメートルに換算した $1.6\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「ロ」の銅導線の抵抗
「ロ」の銅導線は、断面積 $8\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ロ}} =\rho\times\dfrac{\color{#ff3333}{20}}{\color{#ff3333}{8\times 10^{-6}}}$ …⑤ (「ロ」の値を代入した)
$=\dfrac{20\rho}{8\times 10^{-6}}$
$=\dfrac{20\rho}{8}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$=2.5\rho\times 10^6 =2.5\times 10^6\rho$
$\therefore R_{\,\text{ロ}} =2.5\times 10^6\rho$
⑤の断面積 $S$ には、断面積 $8$[$\mathrm{mm^2}$]を平方メートルに換算した $8\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ハ」の銅導線の抵抗
「ハ」の銅導線は、直径 $3.2\,\mathrm{mm}$ 、長さ $10\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{ハ}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{10}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{3.2\times 10^{-3}}\right)^2}$ …⑥ (「ハ」の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{40\rho}{3.14\times 3.2^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{40\rho}{32.2\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{40\rho}{32.2}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 1.24\rho\times 10^6 =1.24\times 10^6\rho$
$\therefore R_{\,\text{ハ}} =1.24\times 10^6\rho$
⑥の直径 $D$ には、直径 $3.2$[$\mathrm{mm}$]をメートルに換算した $3.2\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「ニ」の銅導線の抵抗
「ニ」の銅導線は、断面積 $5.5\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ニ}} =\rho\times\dfrac{\color{#ff3333}{20}}{\color{#ff3333}{5.5\times 10^{-6}}}$ …⑦ (「ニ」の値を代入した)
$=\dfrac{20\rho}{5.5\times 10^{-6}}$
$=\dfrac{20\rho}{5.5}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 3.64\rho\times 10^6 =3.64\times 10^6\rho$
$\therefore R_{\,\text{ニ}} =\color{#ff3333}{3.64\times 10^6\rho}$
⑦の断面積 $S$ には、断面積 $5.5$[$\mathrm{mm^2}$]を平方メートルに換算した $5.5\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
以上より、問題文の銅導線と抵抗値が最も近いものは「ニ」になります。
解答:ニ
問題2の別解①(問題の銅導線の直径を断面積に換算して比較する方法)
この問題2を、問題1の別解①の解き方(問題の銅導線の直径を断面積に換算して比較する方法)でも解いてみましょう。
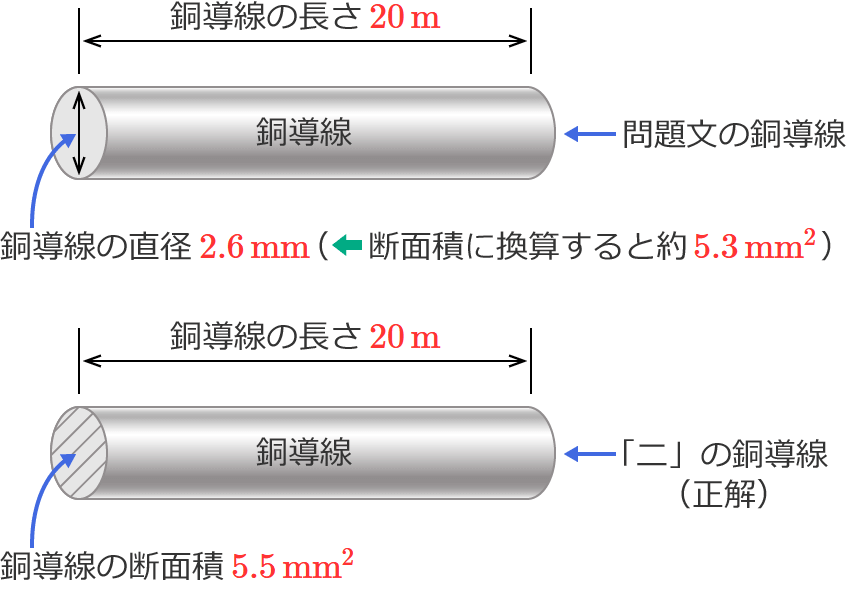
問題文の銅導線の直径は $2.6\,\mathrm{mm}$ なので、これを断面積[$\mathrm{mm^2}$]に換算してみると次のようになります。
問題文の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{2.6}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 1.3^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 1.69 \fallingdotseq 5.3$
$\therefore$ 問題文の銅導線の断面積 $\fallingdotseq \color{#ff3333}{5.3\,\mathrm{mm^2}}$
なので、直径を断面積に換算した問題文の銅導線は、断面積約 $\boldsymbol{5.3\,\mathrm{mm^2}}$ 、長さ $\boldsymbol{20\,\mathrm{m}}$になります。
これと抵抗値が最も近くなるのは選択肢のどの銅導線か、「イ」から見てみましょう。(ぱっとみ、「ニ」が正解っぽいけど…。)
イ.直径 $1.6\,\mathrm{mm}$ 、長さ $40\,\mathrm{m}$ (「イ」の銅導線)
「イ」の銅導線の直径を断面積に換算してみると、
「イ」の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{1.6}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 0.8^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 0.64 \fallingdotseq 2.0$
$\therefore$ 「イ」の銅導線の断面積 $\fallingdotseq 2.0\,\mathrm{mm^2}$
となるので、「イ」の銅導線は、問題文の銅導線よりも断面積は小さく、長さは2倍になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが2倍なら断面積も2倍くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「イ」の銅導線の断面積は約 $2.0\,\mathrm{mm^2}$ …。
長さが2倍なのに断面積は小さくなっているので、これは明らかに違いますね。
次いってみましょう。
ロ.断面積 $8\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ (「ロ」の銅導線)
「ロ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは同じですね。
長さが同じなら断面積も同じくらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ロ」の銅導線の断面積は $8\,\mathrm{mm^2}$ …。
これは、違うっぽいですね。
次いってみましょう。
ハ.直径 $3.2\,\mathrm{mm}$ 、長さ $10\,\mathrm{m}$ (「ハ」の銅導線)
「ハ」の銅導線の直径を断面積に換算してみると、
「ハ」の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{3.2}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 1.6^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 2.56 \fallingdotseq 8.0$
$\therefore$ 「ハ」の銅導線の断面積 $\fallingdotseq 8.0\,\mathrm{mm^2}$
となるので、「ハ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは1/2倍(半分)になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが1/2倍(半分)なら断面積も1/2倍(半分)くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ハ」の銅導線の断面積は約 $8.0\,\mathrm{mm^2}$ …。
長さが1/2倍(半分)なのに断面積は大きくなっているので、これは明らかに違いますね。
次いってみましょう。
ニ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $20\,\mathrm{m}$ (「ニ」の銅導線)
「ニ」の銅導線は、問題文の銅導線とほぼ同じくらいの断面積で、長さは同じですね。
長さが同じで、断面積がほぼ同じなので、正解はこれ!ですね。
以上より、問題文の銅導線と抵抗値が最も近いものは「ニ」になります。
問題2の場合は選択肢にも直径の銅導線があるので、問題1よりも少し計算が増えますね。(問題の銅導線の直径を断面積に直したら、選択肢をみてパッと答えを選んでもいいような…、それはやっちゃだめなような…。)
解答:ニ
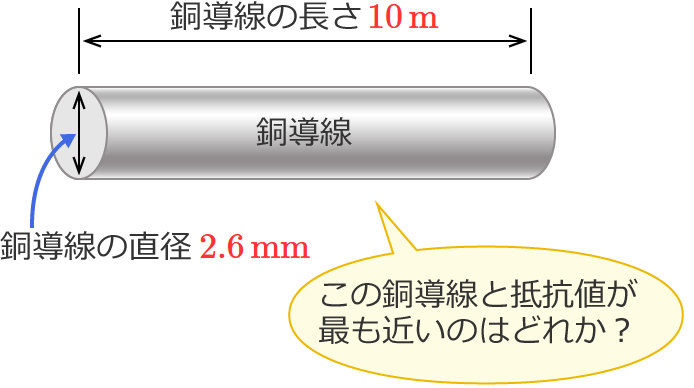
直径 $2.6\,\mathrm{mm}$ 、長さ $10\,\mathrm{m}$ の銅導線と抵抗値が最も近い同材質の銅導線は。
イ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$
ロ.断面積 $8\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$
ハ.直径 $1.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$
ニ.直径 $3.2\,\mathrm{mm}$ 、長さ $5\,\mathrm{m}$
出題:令和元年度下期問2平成30年度下期問3平成28年度下期問3平成25年度下期問3平成21年度問4
解き方
問題3も問題1とほぼ同じ問題で、問題1と問題3の違いは、選択肢に直径の銅導線があるかないかくらいです(問題2とは数値が違うだけ)。問題1と同じような解き方で解くことができますので、問題1の解き方と同じように解いてみます。
問題文に同材質の銅導線と書いてあるので、どの銅導線も抵抗率は同じです。なので、抵抗率をすべて $\rho$[$\Omega\,\cdotp\mathrm{m}$]として、それぞれの銅導線の抵抗を求めます。
各銅導線の抵抗を求めるときは、銅導線の太さが断面積の場合は「電線の太さが断面積の電線の抵抗の公式」(次の①式)、銅導線の太さが直径の場合は「電線の太さが直径の電線の抵抗の公式」(次の②式)を使います。
$R=\rho\dfrac{L}{S}$ …① (電線の太さが断面積の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $S$:電線の断面積[$\mathrm{m^2}$]
$R=\dfrac{4\rho L}{\pi D^2}$ …② (電線の太さが直径の電線の抵抗の公式)
$R$:電線の抵抗[$\Omega$] $\rho$:電線の抵抗率[$\Omega\,\cdotp\mathrm{m}$] $L$:電線の長さ[$\mathrm{m}$] $D$:電線の直径[$\mathrm{m}$]
問題文の銅導線の抵抗
問題文の銅導線は、直径 $2.6\,\mathrm{mm}$ 、長さ $10\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{問題文}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{10}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{2.6\times 10^{-3}}\right)^2}$ …③ (問題文の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{40\rho}{3.14\times 2.6^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{40\rho}{21.2\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{40\rho}{21.2}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 1.89\rho\times 10^6 =1.89\times 10^6\rho$
$\therefore R_{\,\text{問題文}} =\color{#ff3333}{1.89\times 10^6\rho}$
③の直径 $D$ には、直径 $2.6$[$\mathrm{mm}$]をメートルに換算した $2.6\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「イ」の銅導線の抵抗
「イ」の銅導線は、断面積 $5.5\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{イ}} =\rho\times\dfrac{\color{#ff3333}{10}}{\color{#ff3333}{5.5\times 10^{-6}}}$ …④ (「イ」の値を代入した)
$=\dfrac{10\rho}{5.5\times 10^{-6}}$
$=\dfrac{10\rho}{5.5}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 1.82\rho\times 10^6 =1.82\times 10^6\rho$
$\therefore R_{\,\text{イ}} =\color{#ff3333}{1.82\times 10^6\rho}$
④の断面積 $S$ には、断面積 $5.5$[$\mathrm{mm^2}$]を平方メートルに換算した $5.5\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ロ」の銅導線の抵抗
「ロ」の銅導線は、断面積 $8\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$ です。銅導線の太さが断面積なので、①式の「電線の太さが断面積の電線の抵抗の公式」を使って求めます。
$R=\rho\dfrac{L}{S}$ (①式)
$R_{\,\text{ロ}} =\rho\times\dfrac{\color{#ff3333}{10}}{\color{#ff3333}{8\times 10^{-6}}}$ …⑤ (「ロ」の値を代入した)
$=\dfrac{10\rho}{8\times 10^{-6}}$
$=\dfrac{10\rho}{8}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$=1.25\rho\times 10^6 =1.25\times 10^6\rho$
$\therefore R_{\,\text{ロ}} =1.25\times 10^6\rho$
⑤の断面積 $S$ には、断面積 $8$[$\mathrm{mm^2}$]を平方メートルに換算した $8\times 10^{-6}$[$\mathrm{m^2}$]の値を代入しています。
「ハ」の銅導線の抵抗
「ハ」の銅導線は、直径 $1.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{ハ}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{20}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{1.6\times 10^{-3}}\right)^2}$ …⑥ (「ハ」の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{80\rho}{3.14\times 1.6^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{80\rho}{8.04\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{80\rho}{8.04}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 9.95\rho\times 10^6 =9.95\times 10^6\rho$
$\therefore R_{\,\text{ハ}} =9.95\times 10^6\rho$
⑥の直径 $D$ には、直径 $1.6$[$\mathrm{mm}$]をメートルに換算した $1.6\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
「ニ」の銅導線の抵抗
「ニ」の銅導線は、直径 $3.2\,\mathrm{mm}$ 、長さ $5\,\mathrm{m}$ です。銅導線の太さが直径なので、②式の「電線の太さが直径の電線の抵抗の公式」を使って求めます。
$R=\dfrac{4\rho L}{\pi D^2}$ (②式)
$R_{\,\text{ニ}} \fallingdotseq\dfrac{4\rho\times \color{#ff3333}{5}}{\color{#ff3333}{3.14}\times\left( \color{#ff3333}{3.2\times 10^{-3}}\right)^2}$ …⑦ (「ニ」の値と円周率 $\pi\fallingdotseq 3.14$ を代入した)
$=\dfrac{20\rho}{3.14\times 3.2^2\times\left( 10^{-3}\right)^2}$
$\fallingdotseq\dfrac{20\rho}{32.2\times 10^{-6}}$ ($10^{-3}$ の2乗は $10^{-6}$ になります)
$=\dfrac{20\rho}{32.2}\times 10^6$ ($\dfrac{1}{10^{-6}}$ は $10^6$ になります)
$\fallingdotseq 0.62\rho\times 10^6 =0.62\times 10^6\rho$
$\therefore R_{\,\text{ニ}} =0.62\times 10^6\rho$
⑦の直径 $D$ には、直径 $3.2$[$\mathrm{mm}$]をメートルに換算した $3.2\times 10^{-3}$[$\mathrm{m}$]の値を代入しています。
以上より、問題文の銅導線と抵抗値が最も近いものは「イ」になります。
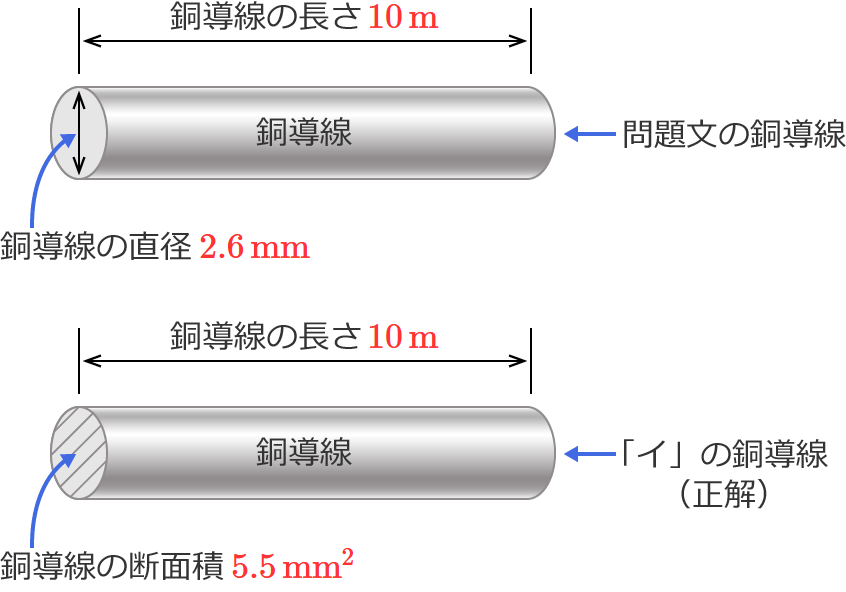
解答:イ
問題3の別解①(問題の銅導線の直径を断面積に換算して比較する方法)
この問題3を、問題1の別解①の解き方(問題の銅導線の直径を断面積に換算して比較する方法)でも解いてみましょう。
問題文の銅導線の直径は $2.6\,\mathrm{mm}$ なので、これを断面積[$\mathrm{mm^2}$]に換算してみると次のようになります。
問題文の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{2.6}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 1.3^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 1.69 \fallingdotseq 5.3$
$\therefore$ 問題文の銅導線の断面積 $\fallingdotseq \color{#ff3333}{5.3\,\mathrm{mm^2}}$
なので、直径を断面積に換算した問題文の銅導線は、断面積約 $\boldsymbol{5.3\,\mathrm{mm^2}}$ 、長さ $\boldsymbol{10\,\mathrm{m}}$になります。
これと抵抗値が最も近くなるのは選択肢のどの銅導線か、「イ」から見てみましょう。(ぱっとみ、「イ」が正解っぽいけど…。)
イ.断面積 $5.5\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$ (「イ」の銅導線)
「イ」の銅導線は、問題文の銅導線とほぼ同じくらいの断面積で、長さは同じですね。
長さが同じで、断面積がほぼ同じなので、正解はこれ!になりそうですね。
いちおう、他も見てみましょう。
ロ.断面積 $8\,\mathrm{mm^2}$ 、長さ $10\,\mathrm{m}$ (「ロ」の銅導線)
「ロ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは同じですね。
長さが同じなら断面積も同じくらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ロ」の銅導線の断面積は $8\,\mathrm{mm^2}$ …。
これは、違うっぽいですね。
次いってみましょう。
ハ.直径 $1.6\,\mathrm{mm}$ 、長さ $20\,\mathrm{m}$ (「ハ」の銅導線)
「ハ」の銅導線の直径を断面積に換算してみると、
「ハ」の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{1.6}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 0.8^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 0.64 \fallingdotseq 2.0$
$\therefore$ 「ハ」の銅導線の断面積 $\fallingdotseq 2.0\,\mathrm{mm^2}$
となるので、「ハ」の銅導線は、問題文の銅導線よりも断面積は小さく、長さは2倍になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが2倍なら断面積も2倍くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ハ」の銅導線の断面積は約 $2.0\,\mathrm{mm^2}$ …。
長さが2倍なのに断面積は小さくなっているので、これは明らかに違いますね。
次いってみましょう。
ニ.直径 $3.2\,\mathrm{mm}$ 、長さ $5\,\mathrm{m}$ (「ニ」の銅導線)
「ニ」の銅導線の直径を断面積に換算してみると、
「ニ」の銅導線の断面積 $=\pi\times\left( \dfrac{\color{#ff3333}{3.2}}{2}\right)^2$ (円の面積の公式を使った)
$\fallingdotseq \color{#ff3333}{3.14}\times 1.6^2$ ($\pi$ に $3.14$ を代入した)
$=3.14\times 2.56 \fallingdotseq 8.0$
$\therefore$ 「ニ」の銅導線の断面積 $\fallingdotseq 8.0\,\mathrm{mm^2}$
となるので、「ニ」の銅導線は、問題文の銅導線よりも断面積は大きく、長さは1/2倍(半分)になっていますね。
電線の抵抗は、長さに比例して、断面積に反比例するので、長さが1/2倍(半分)なら断面積も1/2倍(半分)くらいになっていないと抵抗値は同じくらいにはなりませんね。問題文の銅導線の断面積は約 $5.3\,\mathrm{mm^2}$ 、「ニ」の銅導線の断面積は約 $8.0\,\mathrm{mm^2}$ …。
長さが1/2倍(半分)なのに断面積は大きくなっているので、これは明らかに違いますね。
以上より、問題文の銅導線と抵抗値が最も近いものは「イ」になります。(問題の銅導線の直径を断面積に直したら、選択肢をみてパッと答えを選んでもいいような…、でもでもそれはやっちゃだめなような…。)
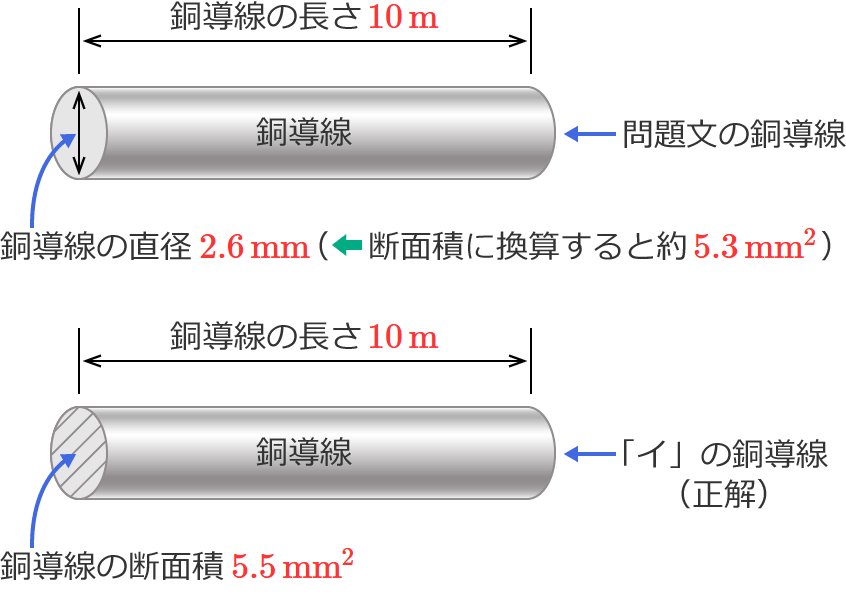
解答:イ
抵抗値が最も近い同材質の銅導線を求める計算問題の解き方の解説は以上になりますが、抵抗値が最も近い同材質の銅導線を求める計算問題を解くためには、電線の抵抗の公式の知識が必要になります。
このページに掲載している電線の抵抗の公式は、第二種電気工事士学科試験で出題されている他の抵抗の計算問題を解くときにもよく使う基本公式ですので、必ずおぼえておくようにしましょう。基本は大事!
スポンサーリンク
スポンサーリンク
第二種電気工事士学科試験の計算問題の解き方のまとめページはこちら
⇒ 第二種電気工事士学科試験の計算問題の解き方
導線の抵抗率を表わす式を求める計算問題の解き方 ←BACK
NEXT→ 2本の銅線の抵抗の比を求める計算問題の解き方
スポンサーリンク
抵抗値が最も近い同材質の銅導線を求める計算問題の解き方 関連ページ
- 抵抗を示す式を求める計算問題の解き方
- 第二種電気工事士学科試験で出題されている「抵抗を示す式を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
- 導線の電気抵抗を表わす式を求める計算問題の解き方
- 第二種電気工事士学科試験で出題されている「導線の電気抵抗を表わす式を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
- 導線の抵抗率を表わす式を求める計算問題の解き方
- 第二種電気工事士学科試験で出題されている「導線の抵抗率を表わす式を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。
- 2本の銅線の抵抗の比を求める計算問題の解き方
- 第二種電気工事士学科試験で出題されている「2本の銅線の抵抗の比を求める計算問題」の解き方について解説しています。問題には過去問題を使っていますので、過去問題の勉強にもなると思います。問題の解き方の他に、問題を解くために必要な基礎知識などについても解説していますので、計算問題の勉強に活用してみてください。


