スポンサーリンク
ベルヌーイの定理
※ページ内にPR・広告が含まれる場合があります。
次のような水圧管を流れる水と、ある基準レベルを考えます。
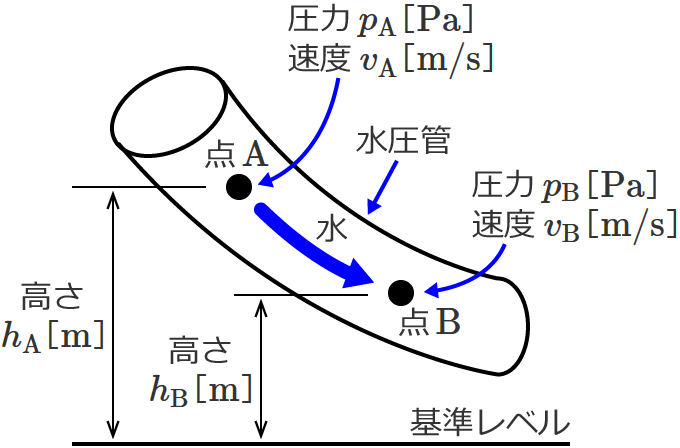
ここで、
$h_\mathrm{A}$ :点 $\mathrm{A}$ での水の高さ [$ \mathrm{m} $]
$p_\mathrm{A}$ :点 $\mathrm{A}$ での圧力 [$ \mathrm{Pa} $]
$v_\mathrm{A}$ :点 $\mathrm{A}$ での水の流速 [$ \mathrm{m / s} $]
$h_\mathrm{B}$ :点 $\mathrm{B}$ での水の高さ [$ \mathrm{m} $]
$p_\mathrm{B}$ :点 $\mathrm{B}$ での圧力 [$ \mathrm{Pa} $]
$v_\mathrm{B}$ :点 $\mathrm{B}$ での水の流速 [$ \mathrm{m / s} $]
です。
水頭には位置水頭、速度水頭、圧力水頭がありますが、摩擦損失が無いものと仮定すると、上図のような点 $\mathrm{A}$ と点 $\mathrm{B}$ において、点 $\mathrm{A}$ での3つの水頭の和と点 $\mathrm{B}$ での3つの水頭の和は等しくなります。
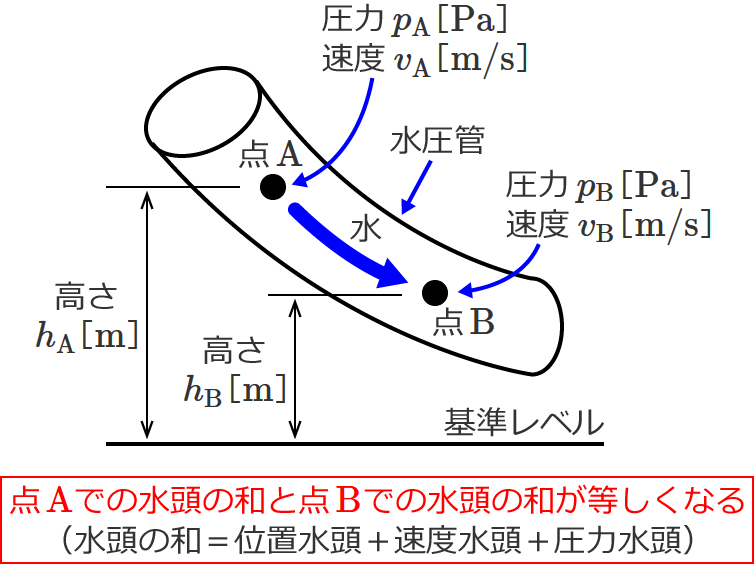
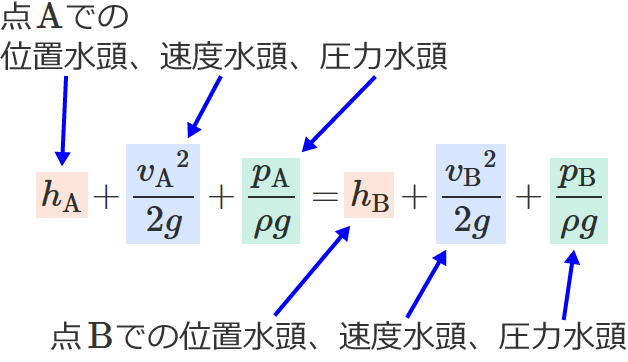
これをベルヌーイの定理といい、水の密度を $\rho$[$ \mathrm{kg / m^3} $]、重力加速度を $g$[$ \mathrm{m / s^2} $]とすると、点 $\mathrm{A}$ と点 $\mathrm{B}$ について次式が成り立ちます。
$\therefore h_\mathrm{A} +\dfrac{{v_\mathrm{A}}^2}{2g} +\dfrac{p_\mathrm{A}}{\rho g}$ $=h_\mathrm{B} +\dfrac{{v_\mathrm{B}}^2}{2g} +\dfrac{p_\mathrm{B}}{\rho g}$
スポンサーリンク
スポンサーリンク
スポンサーリンク
ベルヌーイの定理 関連ページ
- 水力発電所と水車の種類
- 水力発電の「水力発電所と水車の種類」についてまとめたページです。「水力発電所と水車の種類」は第三種電気主任技術者試験(電験三種)でもよく出題される重要な項目です。
- 水力発電所の構成と出力
- 水力発電の「水力発電所の構成と出力」についてまとめたページです。「水力発電所の構成と出力」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 水力発電所の有効落差と損失落差
- 水力発電の「水力発電所の有効落差と損失落差」についてまとめたページです。「水力発電所の有効落差と損失落差」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 水力発電所の出力と有効落差の関係
- 水力発電の「水力発電所の出力と有効落差の関係」についてまとめたページです。「水力発電所の出力と有効落差の関係」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 比速度
- 水力発電の「比速度」についてまとめたページです。「比速度」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 速度調定率
- 水力発電の「速度調定率」についてまとめたページです。「速度調定率」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 周波数と発電機出力の関係(ガバナ特性)
- 水力発電の「周波数と発電機出力の関係(ガバナ特性)」についてまとめたページです。「周波数と発電機出力の関係(ガバナ特性)」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 水頭
- 水力発電の「水頭」についてまとめたページです。「水頭」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 河川の年間平均流量
- 水力発電の「河川の年間平均流量」についてまとめたページです。
- 揚水発電
- 水力発電の「揚水発電」についてまとめたページです。「揚水発電」は第三種電気主任技術者試験(電験三種)でも出題される項目です。


