スポンサーリンク
直流発電機の誘導起電力
※ページ内にPR・広告が含まれる場合があります。
直流発電機の誘導起電力の公式
直流発電機の誘導起電力 $E$ を与える式は、
$E$ :直流発電機の誘導起電力 [$ \mathrm{V} $]
$a$ :並列回路数(重ね巻の場合 $a=p$、波巻の場合 $a=2$)
$p$ :磁極数
$Z$ :電機子の導体総数
$N$ :電機子の回転速度 [$ \mathrm{min^{-1}} $]
とすると、次式で与えられます。
$E=\dfrac{pZ}{60a} \phi N$ [$ \mathrm{V} $]
スポンサーリンク
直流発電機の誘導起電力の式の導出
直流発電機の誘導起電力の式は、次のようにすると導出できます。
ある $n$[本]の導体が時間 $\varDelta t$[$ \mathrm{s} $]の間に $\varDelta \phi$[$ \mathrm{Wb} $]の磁束を切るとき、このときに発生する誘導起電力 $e$ の大きさは次式で与えられます。
$e=n \dfrac{\varDelta \phi}{\varDelta t}$ [$ \mathrm{V} $] …①
ここで、①式の $\dfrac{\varDelta \phi}{\varDelta t}$ は、$\varDelta t = 1$[$ \mathrm{s} $]とすれば $\dfrac{\varDelta \phi}{\varDelta t}$ は1秒間の磁束 $\phi$ の変化量ということになるので、例えば次のように磁束密度 $B$[$ \mathrm{T} $]の中で、長さ $l$[$ \mathrm{m} $]の導体が速度 $v$[$ \mathrm{m / s} $]で移動している場合、$\dfrac{\varDelta \phi}{\varDelta t}$ は、$\dfrac{\varDelta \phi}{\varDelta t} = B \cdot vl = Blv$ と表わされます。
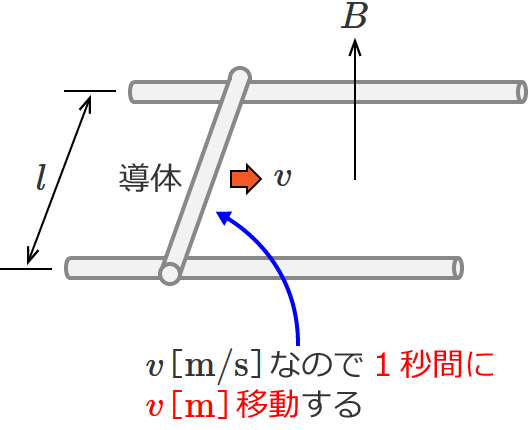
移動速度 $v$ は導体が1秒間に進む距離なので、$l \times v$ が1秒間に磁束を切る面積になります。
したがって、 $n$[本]の導体が磁束を切る場合の誘導起電力 $e$ の大きさは、次のようになります。
$e=nBlv$ [$ \mathrm{V} $] …②
次に、②式の $n$、$B$、$v$ について、直流発電機と対応させて考えてみます。
直流発電機の電機子巻線の導体総数を $Z$、並列回路数を $a$ とすると、直列導体数 $n$ は、
$n = \dfrac{Z}{a}$ …③ となります。
また、電機子の直径を $D$[$ \mathrm{m} $]、長さを $l$[$ \mathrm{m} $]、磁極数を $p$、毎極の有効磁束を $ \phi $[$ \mathrm{Wb} $]とすれば、電機子の周辺の平均磁束密度 $B$ は、
$B = \dfrac{\text{全磁束}}{\text{電機子の周辺の面積}} = \dfrac{p \cdot \phi}{\pi D \cdot l}$
$\therefore B = \dfrac{p \phi}{\pi D l}$ [$ \mathrm{T} $] …④ となります。( $\pi D$ は円周で、半径を $r$ とすると $\pi D = 2 \pi r$ です。)
速度 $v$ については、電機子の半径を $r$[$ \mathrm{m} $]、電機子の回転角速度を $\omega$[$ \mathrm{rad / s} $]とすれば、$v=r \omega$ なので、これを電機子の直径 $D$、電機子の回転速度 $N$[$ \mathrm{min^{-1}} $]で表わすと次のようになります。( $f$ は周波数で、$\omega = 2 \pi f$ です。)
$v = r \omega = r \cdot 2 \pi f = 2 \pi r \cdot f$ $= \pi \cdot 2r \cdot \dfrac{N}{60}$ $= \pi D \dfrac{N}{60}$
$\therefore v = \pi D \dfrac{N}{60}$ [$ \mathrm{m / s} $] …⑤
以上より、③、④、⑤式を②式に代入すると、
$e = nBlv = \dfrac{Z}{a} \cdot \dfrac{p \phi}{\pi D l} \cdot l \cdot \pi D \dfrac{N}{60}$ $= \dfrac{Z p \phi N}{60 a}$ $= \dfrac{p Z}{60 a} \phi N$
$\therefore e = \dfrac{p Z}{60 a} \phi N$
したがって、$e=E$ とすれば、直流発電機の誘導起電力を与える式は次式となります。
$\therefore E = \dfrac{p Z}{60 a} \phi N$ [$ \mathrm{V} $]
スポンサーリンク
スポンサーリンク
誘導起電力については、こちらの電磁誘導のページも参考にしてみてください。
電気のお勉強のTOP ←BACK
NEXT→ 直流分巻電動機の等価回路
スポンサーリンク
直流発電機の誘導起電力 関連ページ
- 直流分巻電動機の等価回路
- 電気機器分野の「直流分巻電動機の等価回路」についてまとめたページです。「直流分巻電動機」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。等価回路の書き方、誘導起電力(逆起電力)、出力、トルクなどの求め方を理解しておきましょう。
- 直流他励電動機の等価回路
- 電気機器分野の「直流他励電動機の等価回路」についてまとめたページです。「直流他励電動機」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。等価回路の書き方、誘導起電力(逆起電力)、回転速度、トルクなどの求め方を理解しておきましょう。
- 誘導電動機の同期速度
- 電気機器の「誘導電動機の同期速度」についてまとめたページです。「誘導電動機の同期速度」は第二種電気工事士試験、第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。同期速度を与える式をおぼえておきましょう。
- 誘導電動機のすべり
- 電気機器の「誘導電動機のすべり」についてまとめたページです。「誘導電動機のすべり」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。すべりを与える式をおぼえておきましょう。
- 誘導電動機のトルク
- 電気機器の「誘導電動機のトルク」についてまとめたページです。「誘導電動機のトルク」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。トルクを与える式をおぼえておきましょう。
- 誘導電動機の固定子巻線抵抗
- 電気機器分野の「誘導電動機の固定子巻線抵抗」についてまとめたページです。「誘導電動機の固定子巻線抵抗」は第二種電気主任技術者試験(電験二種)でも出題される項目です。
- 誘導電動機のL形等価回路
- 電気機器分野の「誘導電動機のL形等価回路(簡易等価回路)」についてまとめたページです。「誘導電動機のL形等価回路」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。L形等価回路の書き方、各損失、出力、効率などの求め方を理解しておきましょう。
- 誘導電動機の無負荷試験
- 電気機器の「誘導電動機の無負荷試験」についてまとめたページです。「誘導電動機の無負荷試験」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。無負荷試験時の等価回路をおぼえておきましょう。
- 誘導電動機の拘束試験
- 電気機器の「誘導電動機の拘束試験」についてまとめたページです。「誘導電動機の拘束試験」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。拘束試験時の等価回路をおぼえておきましょう。
- 誘導電動機のスターデルタ(Y-Δ)始動法
- 電気機器の「誘導電動機のスターデルタ始動法」についてまとめたページです。「誘導電動機のスターデルタ始動法」は第二種電気工事士や第三種電気主任技術者試験(電験三種)の機械科目でも出題される重要で基本的な項目です。
- 同期電動機の等価回路とベクトル図
- 電気機器分野の「同期電動機の等価回路」についてまとめたページです。「同期電動機の等価回路」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。等価回路とベクトル図の書き方をおぼえておきましょう。
- 三相回路の基準インピーダンス・基準電流の式の導出
- 電気機器分野の「三相回路の基準インピーダンス・基準電流の式の導出」についてまとめたページです。「三相回路の基準インピーダンス・基準電流の式」は第三種電気主任技術者試験(電験三種)でも出題される重要な項目です。公式を暗記するだけではなく、式の導出方法をおぼえておきましょう。


