スポンサーリンク
第二種電気工事士学科試験の電圧降下の問題を解くための公式
※ページ内にPR・広告が含まれる場合があります。
第二種電気工事士学科試験の「電圧降下」の計算問題を解くために使う重要な公式とその使い方についてまとめています。
第二種電気工事士学科試験の計算問題を解くためには電気の公式をおぼえておく必要がありますが、公式が苦手という方はそこそこいたりします。
そこで、このページでは第二種電気工事士学科試験の電圧降下の計算問題を解くための重要な公式とその使い方についてまとめてみましたので、試験勉強に活用してみてください。
掲載している公式はどれも重要で計算問題を解くときによく使う公式ですので、掲載されている公式は一通りおぼえておくようにしましょう。
第二種電気工事士学科試験の問題を解くときに使う公式はどれも電気の基本的な公式ですので、公式が苦手な方でも、ちょっとした空き時間などを利用して何度も繰り返し見ていれば、おぼえられるんじゃないかと思います。
スポンサーリンク
単相2線式回路の電圧降下の問題を解くための公式
※単相2線式回路の負荷は抵抗負荷とし、電線の抵抗の大きさはどれも同じとします。
単相2線式回路の電線路の電圧降下の公式
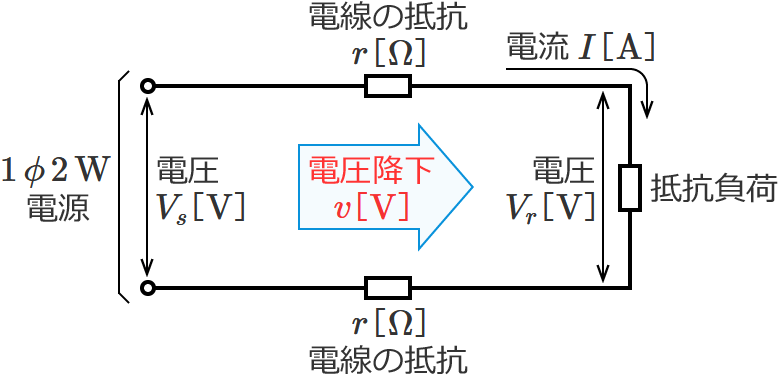
この電圧降下の公式は、単相2線式回路の電線路の電圧降下( $\boldsymbol{V_s-V_r}$ )を求めるときに使う公式です。
①式の公式とその使い方
①式の公式の $I$ に電線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v$ を求めることができます。
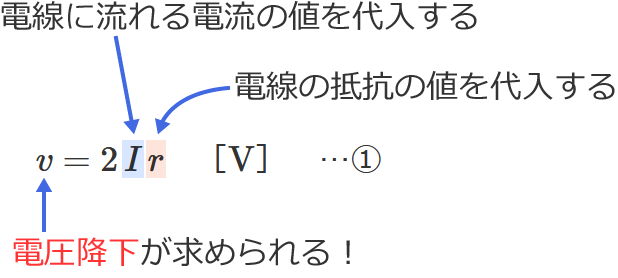
単相2線式回路の電源の電圧の公式
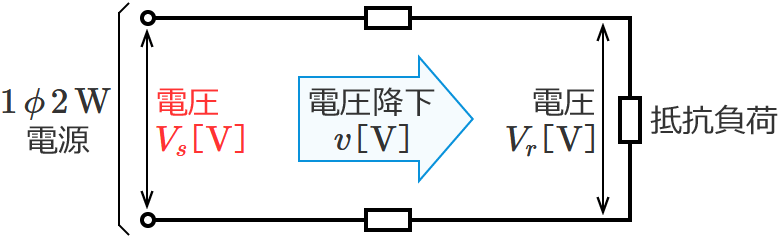
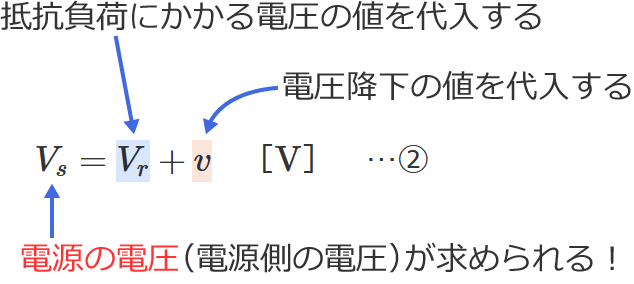
この電圧の公式は、単相2線式回路の「抵抗負荷にかかる電圧」と「電圧降下」から単相2線式回路の電源の電圧(電源側の電圧)を求めるときに使う公式です。
②式の公式とその使い方
②式の公式の $V_r$ に抵抗負荷にかかる電圧の値、$v$ に電圧降下の値を代入すると、電源の電圧(電源側の電圧)$V_s$ を求めることができます。
単相2線式回路の電線の抵抗の公式
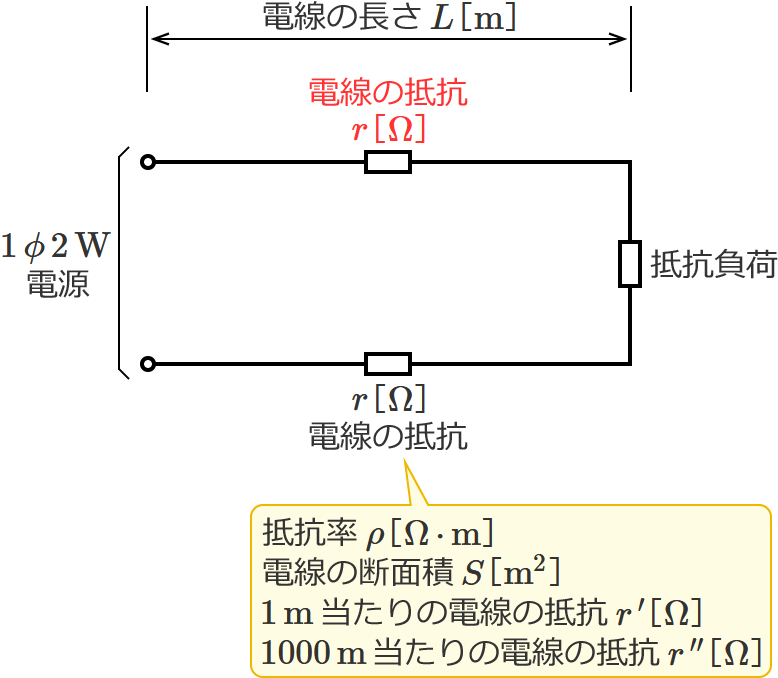
この電線の抵抗の公式は、単相2線式回路の電線1本の抵抗を求めるときに使う公式です。
③式の公式とその使い方
「電線の抵抗率」と「電線の断面積」と「電線の長さ」から電線1本の抵抗を求める場合は、③式の公式を使います。③式の $\rho$ に電線の抵抗率の値、$S$ に電線の断面積の値、$L$ に電線の長さの値を代入すると、電線1本の抵抗 $r$ を求めることができます。

④式の公式とその使い方
「長さ $1\,\mathrm{m}$ 当たりの電線の抵抗」と「電線の長さ」から電線1本の抵抗を求める場合は、④式の公式を使います。④式の $r^{\,\prime}$ に長さ $1\,\mathrm{m}$ 当たりの電線の抵抗の値、$L$ に電線の長さの値を代入すると、電線1本の抵抗 $r$ を求めることができます。
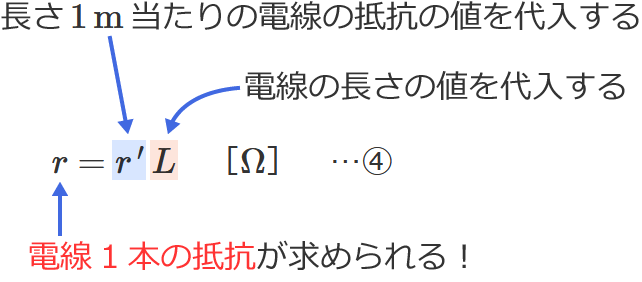
⑤式の公式とその使い方
「長さ $1000\,\mathrm{m}$ 当たりの電線の抵抗」と「電線の長さ」から電線1本の抵抗を求める場合は、⑤式の公式を使います。⑤式の $r^{\,\prime\prime}$ に長さ $1000\,\mathrm{m}$ 当たりの電線の抵抗の値、$L$ に電線の長さの値を代入すると、電線1本の抵抗 $r$ を求めることができます。

単相2線式回路の電線に流れる電流の公式
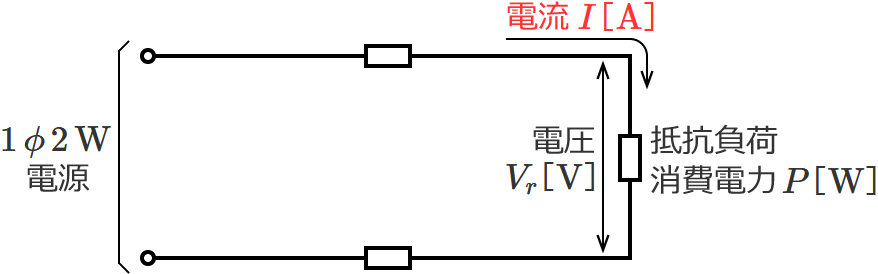
この電流の公式は、単相2線式回路の「抵抗負荷にかかる電圧」と「抵抗負荷の消費電力」から単相2線式回路の電線に流れる電流(=抵抗負荷に流れる電流)を求めるときに使う公式です。
⑥式の公式とその使い方
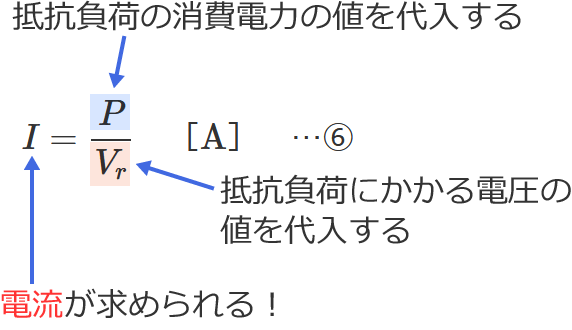
⑥式の公式の $V_r$ に抵抗負荷にかかる電圧の値、$P$ に抵抗負荷の消費電力の値を代入すると、電線に流れる電流 $I$ を求めることができます。
単相2線式回路の電線に流れる電流の公式(抵抗負荷が2つ並列に接続されている場合)
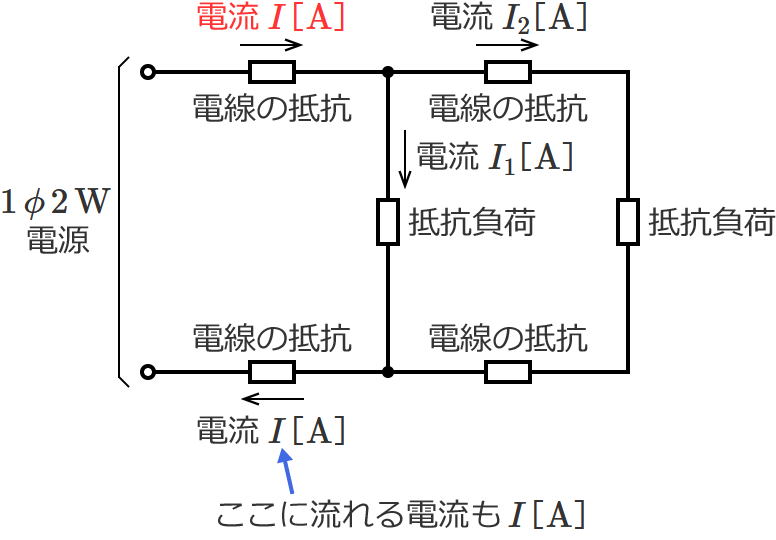
この電流の公式は、単相2線式回路の負荷側に抵抗負荷が2つ並列接続されている回路において、電源側の電線に流れる電流を求めるときに使う公式です。
⑦式の公式とその使い方
⑦式の公式の $I_1$ と $I_2$ にそれぞれの電流の値を代入すると、電源側の電線に流れる電流 $I$ を求めることができます。

スポンサーリンク
スポンサーリンク
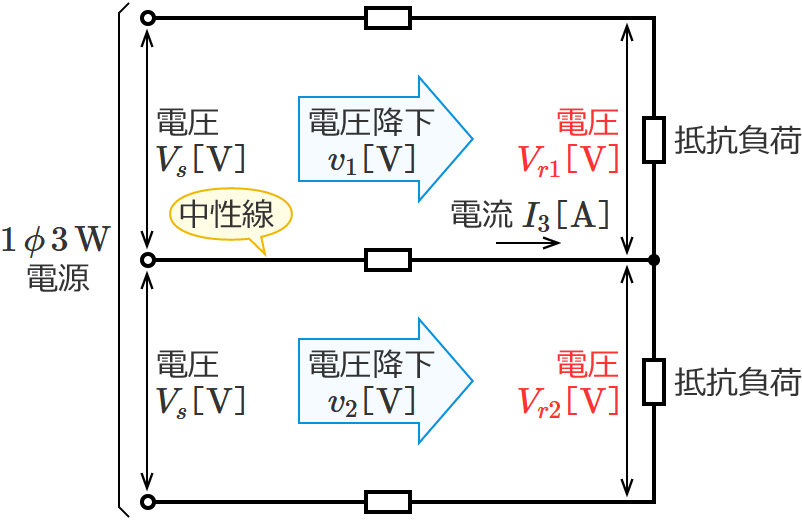
単相3線式回路の電圧降下の問題を解くための公式
※単相3線式回路の負荷は抵抗負荷とし、電線の抵抗の大きさはどれも同じとします。
単相3線式回路の電線路の電圧降下の公式(中性線の電流がゼロの場合※)
※中性線の電流がゼロの場合とは、「上側の抵抗負荷に流れる電流の大きさ」と「下側の抵抗負荷に流れる電流の大きさ」が等しい場合です。
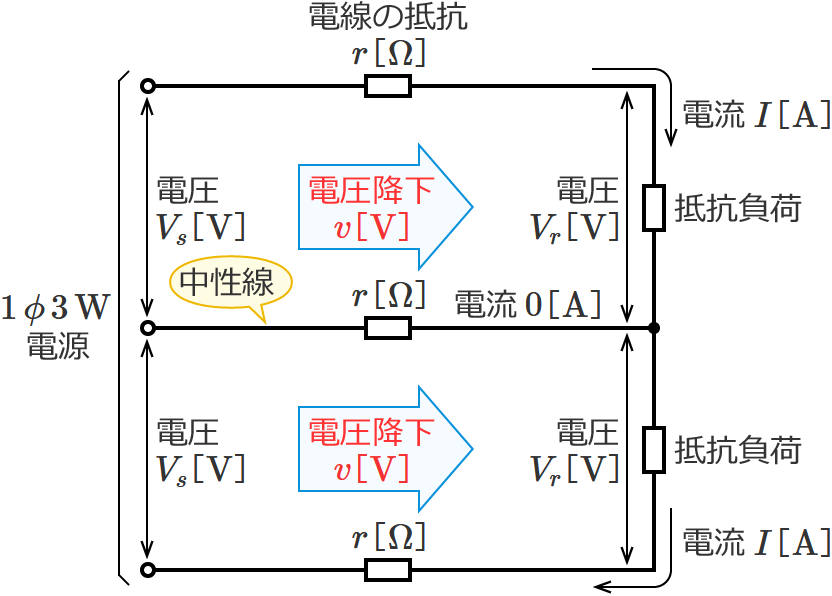
この電圧降下の公式は、中性線の電流がゼロの場合の単相3線式回路の電線路の電圧降下( $\boldsymbol{V_s-V_r}$ )を求めるときに使う公式です。
⑧式の公式とその使い方
⑧式の公式の $I$ に電線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v$ を求めることができます。

単相3線式回路の抵抗負荷にかかる電圧の公式(中性線の電流がゼロの場合)
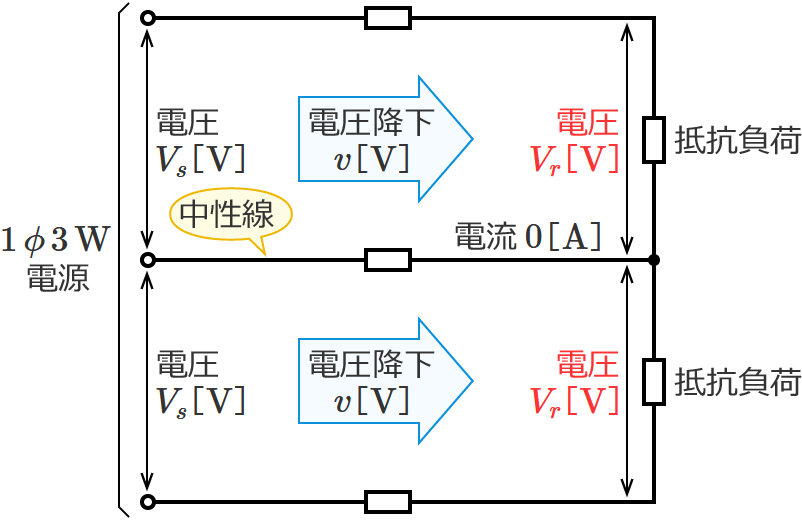
この電圧の公式は、中性線の電流がゼロの場合の単相3線式回路の抵抗負荷にかかる電圧を求めるときに使う公式です。
⑨式の公式とその使い方
⑨式の公式の $V_s$ に電源の電圧の値、$v$ に電圧降下の値を代入すると、抵抗負荷にかかる電圧 $V_r$ を求めることができます。
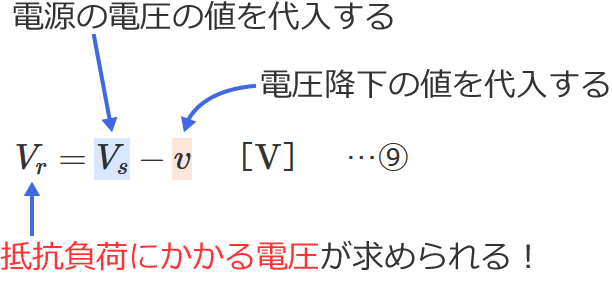
ちなみに、⑨式の公式の $v$ に⑧式の電圧降下 $v$ を代入すると、
$V_r=V_s-v=V_s-I\, r$ $\therefore V_r=V_s-I\, r$
となります。
単相3線式回路の中性線に流れる電流の公式(中性線に左向きの電流が流れる場合※)
※中性線に左向きの電流が流れる場合とは、「上側の抵抗負荷に流れる電流」が「下側の抵抗負荷に流れる電流」よりも大きい場合です。
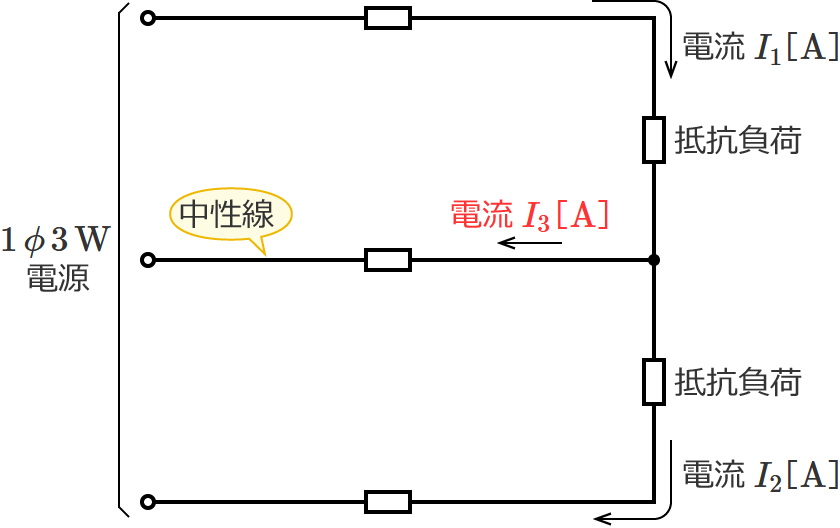
この電流の公式は、中性線に左向きの電流が流れる場合の単相3線式回路の中性線に流れる電流を求めるときに使う公式です。
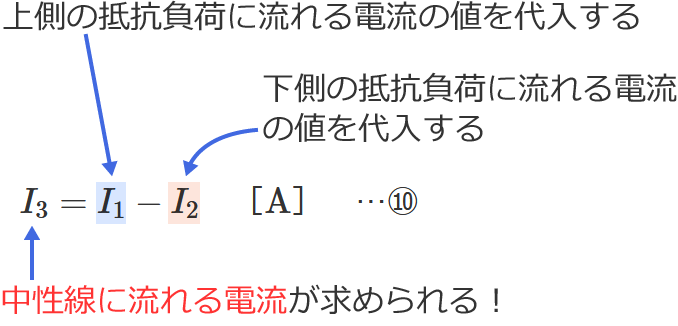
⑩式の公式とその使い方
⑩式の公式の $I_1$ に上側の抵抗負荷に流れる電流の値(=上側の電線に流れる電流の値)、$I_2$ に下側の抵抗負荷に流れる電流の値(=下側の電線に流れる電流の値)を代入すると、中性線に流れる電流 $I_3$ を求めることができます。
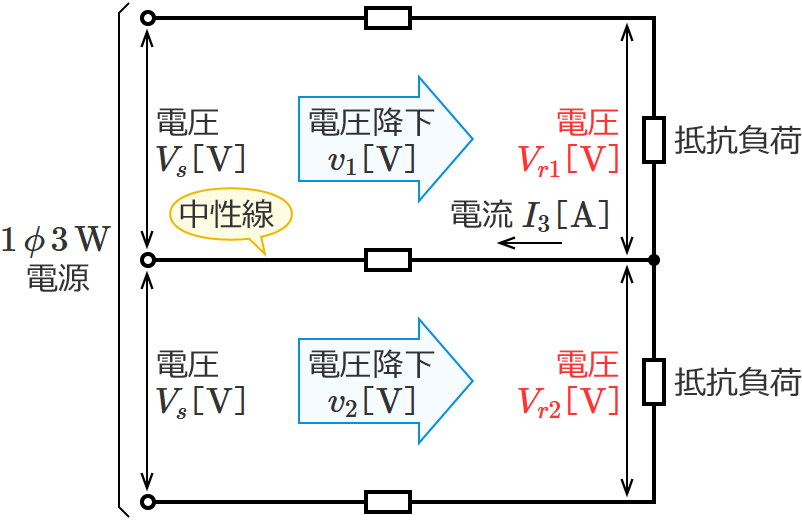
単相3線式回路の電線路の電圧降下の公式(中性線に左向きの電流が流れる場合)
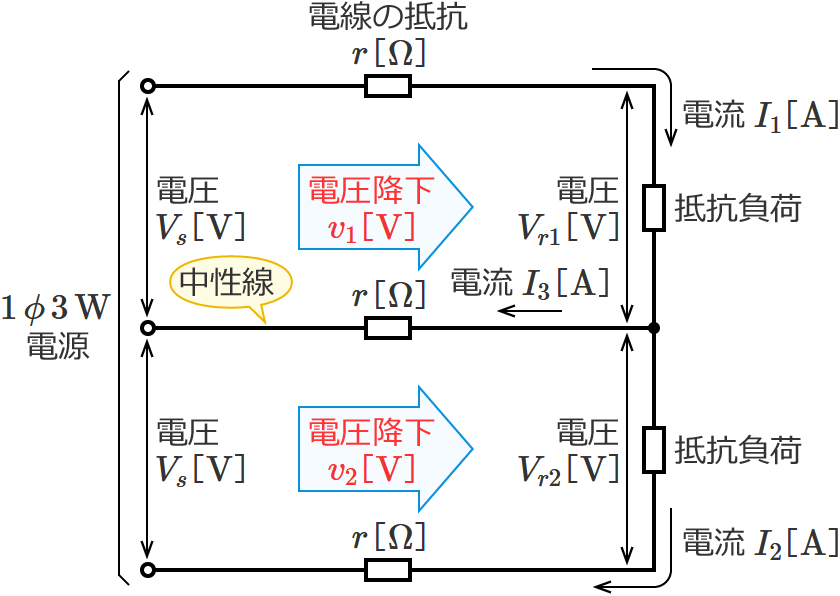
この電圧降下の公式は、中性線に左向きの電流が流れる場合の単相3線式回路の電線路の電圧降下( $\boldsymbol{V_s-V_{r1}}$ 、$\boldsymbol{V_s-V_{r2}}$ )を求めるときに使う公式です。
⑪式の公式とその使い方
⑪式の公式の $I_1$ に上側の電線に流れる電流の値、$I_3$ に中性線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v_1$ を求めることができます。
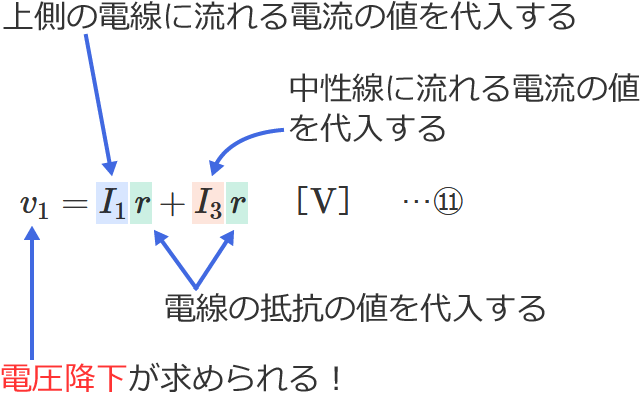
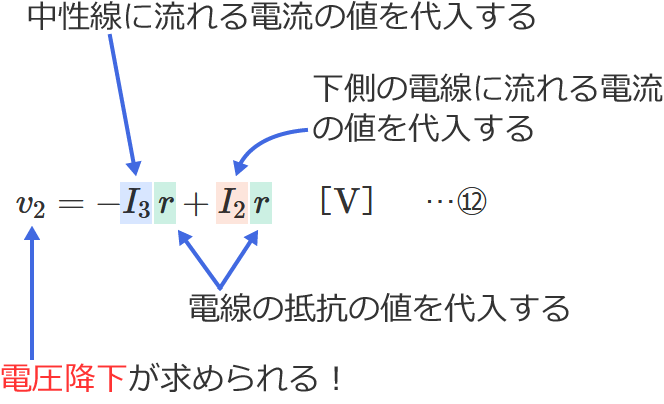
⑫式の公式とその使い方
⑫式の公式の $I_3$ に中性線に流れる電流の値、$I_2$ に下側の電線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v_2$ を求めることができます。
単相3線式回路の抵抗負荷にかかる電圧の公式(中性線に左向きの電流が流れる場合)
この電圧の公式は、中性線に左向きの電流が流れる場合の単相3線式回路の抵抗負荷にかかる電圧を求めるときに使う公式です。
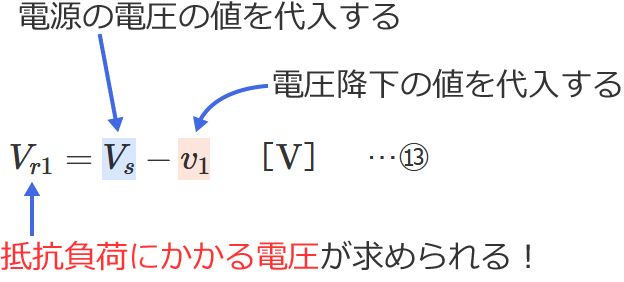
⑬式の公式とその使い方
⑬式の公式の $V_s$ に電源の電圧の値、$v_1$ に電圧降下の値を代入すると、抵抗負荷にかかる電圧 $V_{r1}$ を求めることができます。
ちなみに、⑬式の公式の $v_1$ に⑪式の電圧降下 $v_1$ を代入すると、
$V_{r1}=V_s-v_1=V_s-\left( I_1\, r+I_3\, r\right)$ $=V_s-I_1\, r-I_3\, r$
$\therefore V_{r1}=V_s-I_1\, r-I_3\, r$
となります。
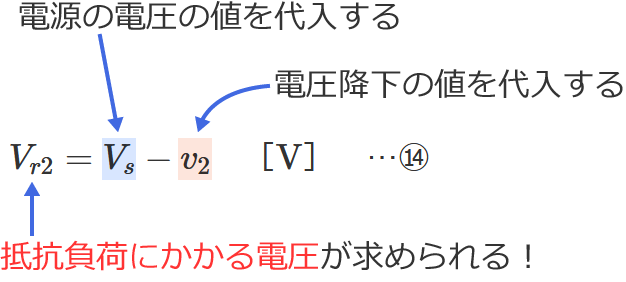
⑭式の公式とその使い方
⑭式の公式の $V_s$ に電源の電圧の値、$v_2$ に電圧降下の値を代入すると、抵抗負荷にかかる電圧 $V_{r2}$ を求めることができます。
ちなみに、⑭式の公式の $v_2$ に⑫式の電圧降下 $v_2$ を代入すると、
$V_{r2}=V_s-v_2=V_s-\left( -I_3\, r+I_2\, r\right)$ $=V_s+I_3\, r-I_2\, r$
$\therefore V_{r2}=V_s+I_3\, r-I_2\, r$
となります。
単相3線式回路の中性線に流れる電流の公式(中性線に右向きの電流が流れる場合※)
※中性線に右向きの電流が流れる場合とは、「上側の抵抗負荷に流れる電流」が「下側の抵抗負荷に流れる電流」よりも小さい場合です。
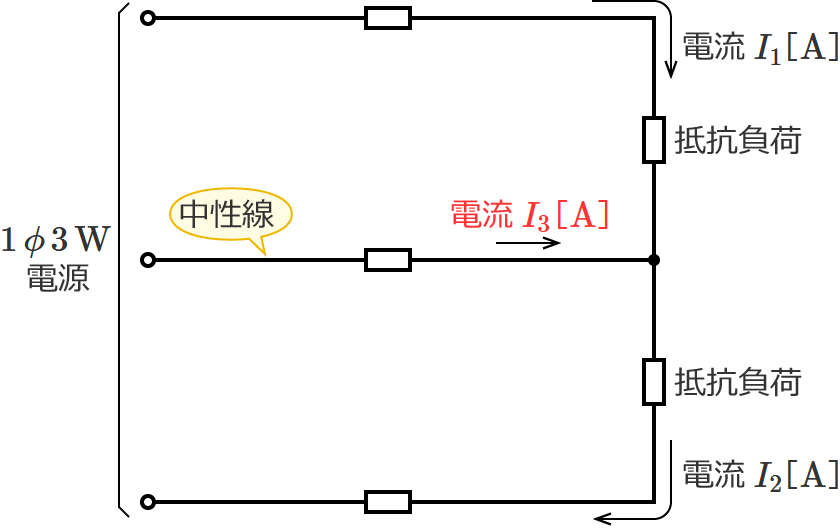
この電流の公式は、中性線に右向きの電流が流れる場合の単相3線式回路の中性線に流れる電流を求めるときに使う公式です。
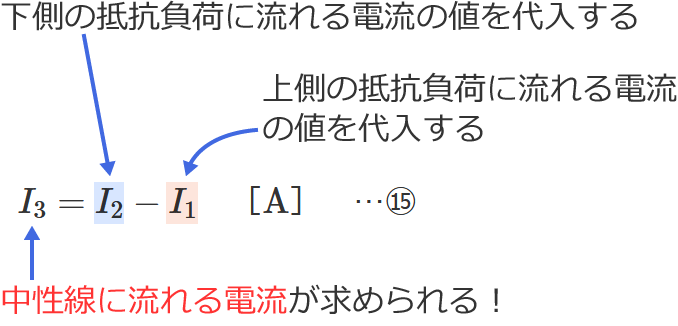
⑮式の公式とその使い方
⑮式の公式の $I_2$ に下側の抵抗負荷に流れる電流の値(=下側の電線に流れる電流の値)、$I_1$ に上側の抵抗負荷に流れる電流の値(=上側の電線に流れる電流の値)を代入すると、中性線に流れる電流 $I_3$ を求めることができます。
単相3線式回路の電線路の電圧降下の公式(中性線に右向きの電流が流れる場合)
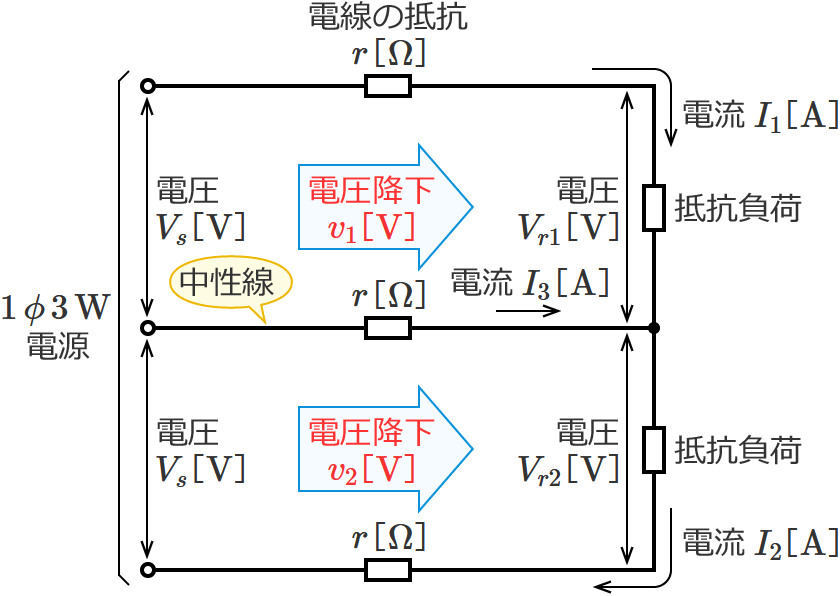
この電圧降下の公式は、中性線に右向きの電流が流れる場合の単相3線式回路の電線路の電圧降下( $\boldsymbol{V_s-V_{r1}}$ 、$\boldsymbol{V_s-V_{r2}}$ )を求めるときに使う公式です。
⑯式の公式とその使い方
⑯式の公式の $I_1$ に上側の電線に流れる電流の値、$I_3$ に中性線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v_1$ を求めることができます。
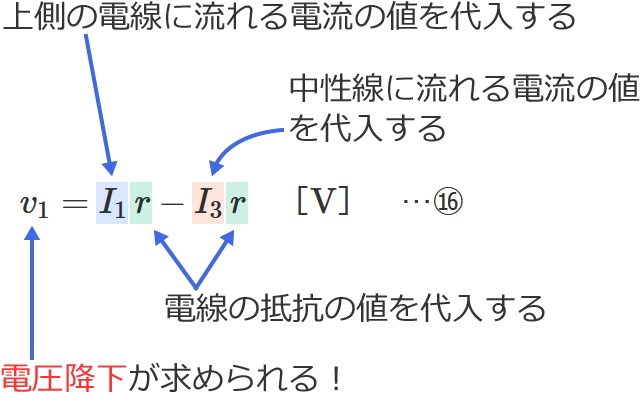
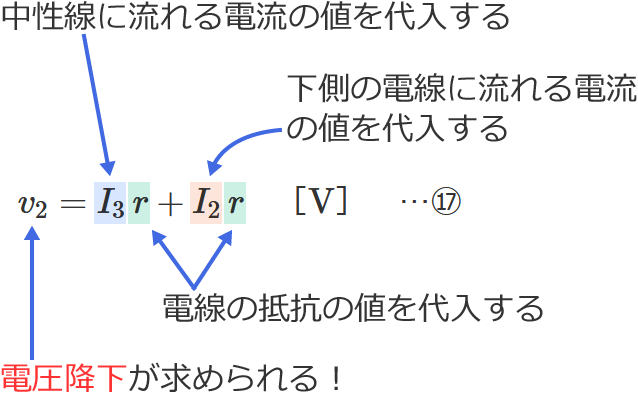
⑰式の公式とその使い方
⑰式の公式の $I_3$ に中性線に流れる電流の値、$I_2$ に下側の電線に流れる電流の値、$r$ に電線の抵抗の値を代入すると、電圧降下 $v_2$ を求めることができます。
単相3線式回路の抵抗負荷にかかる電圧の公式(中性線に右向きの電流が流れる場合)
この電圧の公式は、中性線に右向きの電流が流れる場合の単相3線式回路の抵抗負荷にかかる電圧を求めるときに使う公式です。
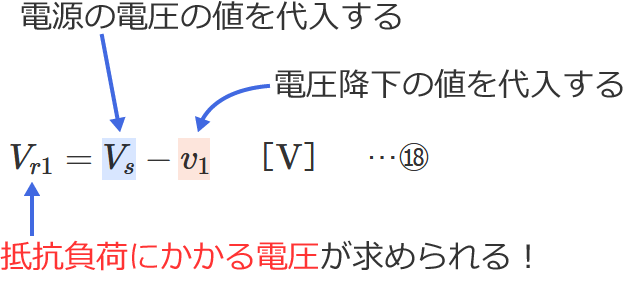
⑱式の公式とその使い方
⑱式の公式の $V_s$ に電源の電圧の値、$v_1$ に電圧降下の値を代入すると、抵抗負荷にかかる電圧 $V_{r1}$ を求めることができます。
ちなみに、⑱式の公式の $v_1$ に⑯式の電圧降下 $v_1$ を代入すると、
$V_{r1}=V_s-v_1=V_s-\left( I_1\, r-I_3\, r\right)$ $=V_s-I_1\, r+I_3\, r$
$\therefore V_{r1}=V_s-I_1\, r+I_3\, r$
となります。
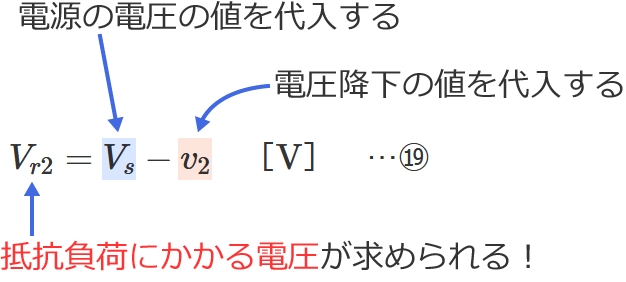
⑲式の公式とその使い方
⑲式の公式の $V_s$ に電源の電圧の値、$v_2$ に電圧降下の値を代入すると、抵抗負荷にかかる電圧 $V_{r2}$ を求めることができます。
ちなみに、⑲式の公式の $v_2$ に⑰式の電圧降下 $v_2$ を代入すると、
$V_{r2}=V_s-v_2=V_s-\left( I_3\, r+I_2\, r\right)$ $=V_s-I_3\, r-I_2\, r$
$\therefore V_{r2}=V_s-I_3\, r-I_2\, r$
となります。
三相3線式回路の電圧降下の問題を解くための公式
※三相3線式回路の負荷は三相抵抗負荷とし、電線の抵抗の大きさはどれも同じとします。
三相3線式回路の電線路の電圧降下の公式
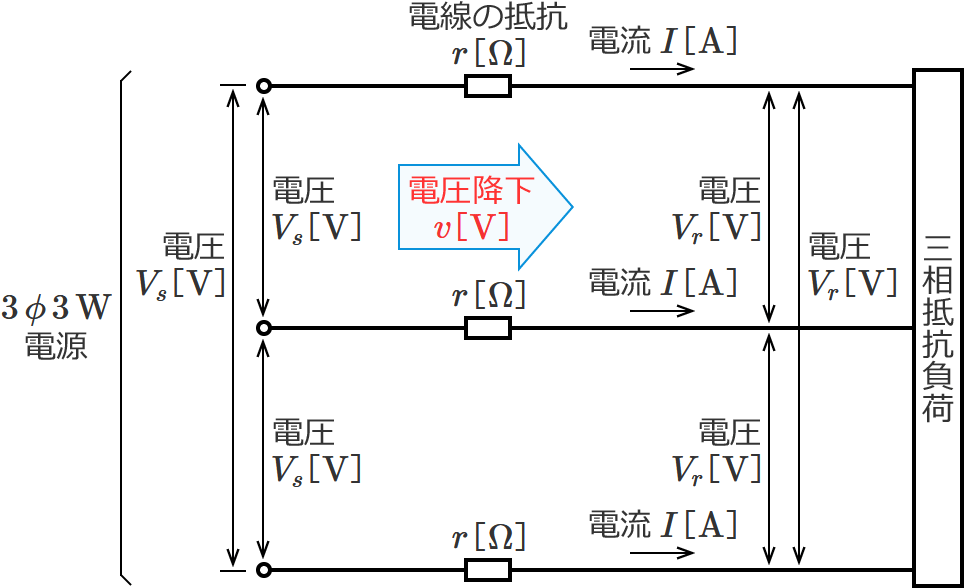
この電圧降下の公式は、三相3線式回路の電線路の電圧降下( $\boldsymbol{V_s-V_r}$ )を求めるときに使う公式です。
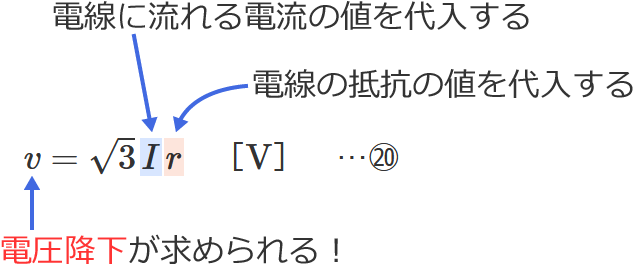
⑳式の公式とその使い方
⑳式の公式の $I$ に電線に流れる電流の値(=線電流の値)、$r$ に電線の抵抗の値を代入すると、電圧降下 $v$ を求めることができます。
電圧降下の問題を解くための公式の一覧表
以上の第二種電気工事士学科試験の電圧降下の問題を解くための公式を一覧表にまとめると、次の表のようになります。
単相2線式回路の公式
| 項目 | 公式 |
|---|---|
| 電圧降下 | $v=2\, I\, r$ |
| 電源の電圧 (電源側の電圧) |
$V_s=V_r+v$ |
| 電線の抵抗 | $r=\rho\dfrac{L}{S}$ |
| $r=r^{\,\prime}\, L$ | |
| $r=\dfrac{r^{\,\prime\prime}}{1000} L$ | |
| 電線に流れる電流 | $I=\dfrac{P}{V_r}$ |
| 電源側の電線に流れる電流 (抵抗負荷が2つ並列の回路) |
$I=I_1+I_2$ |
単相3線式回路の公式(中性線の電流がゼロの場合)
| 項目 | 公式 |
|---|---|
| 電圧降下 | $v=I\, r$ |
| 抵抗負荷にかかる電圧 | $V_r=V_s-v$ |
単相3線式回路の公式(中性線に左向きの電流が流れる場合)
| 項目 | 公式 |
|---|---|
| 中性線に流れる電流 | $I_3=I_1-I_2$ |
| 電圧降下 | $v_1=I_1\, r+I_3\, r$ |
| $v_2=-I_3\, r+I_2\, r$ | |
| 抵抗負荷にかかる電圧 | $V_{r1}=V_s-v_1$ |
| $V_{r2}=V_s-v_2$ |
単相3線式回路の公式(中性線に右向きの電流が流れる場合)
| 項目 | 公式 |
|---|---|
| 中性線に流れる電流 | $I_3=I_2-I_1$ |
| 電圧降下 | $v_1=I_1\, r-I_3\, r$ |
| $v_2=I_3\, r+I_2\, r$ | |
| 抵抗負荷にかかる電圧 | $V_{r1}=V_s-v_1$ |
| $V_{r2}=V_s-v_2$ |
三相3線式回路の公式
| 項目 | 公式 |
|---|---|
| 電圧降下 | $v=\sqrt{3}\, I\, r$ |
計算問題で一問でも多く正解するためにも、頑張って公式をおぼえましょう!
スポンサーリンク
スポンサーリンク
電圧降下についてもうちょっと詳しく勉強したい方は、こちらの配電線の電圧降下のページも参考にしてみましょう。
(第二種電気工事士学科試験の計算問題を解くための公式を一覧表にまとめた重要公式集はこちら。)
スポンサーリンク
第二種電気工事士学科試験の電圧降下の問題を解くための公式 関連ページ
- 第二種電気工事士学科試験の計算問題を解くための重要公式集
- 第二種電気工事士学科試験の計算問題を解くために使う重要な公式についてまとめています。第二種電気工事士学科試験の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の直流回路の問題を解くための公式
- 第二種電気工事士学科試験の「直流回路」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「直流回路」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の合成抵抗の問題を解くための公式
- 第二種電気工事士学科試験の「合成抵抗」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「合成抵抗」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の電線の抵抗の問題を解くための公式
- 第二種電気工事士学科試験の「電線の抵抗」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「電線の抵抗」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の発熱量の問題を解くための公式
- 第二種電気工事士学科試験の「発熱量」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「発熱量」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の比熱の問題を解くための公式
- 第二種電気工事士学科試験の「比熱」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「比熱」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の正弦波交流の問題を解くための公式
- 第二種電気工事士学科試験の「正弦波交流」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「正弦波交流」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の単相交流回路の問題を解くための公式
- 第二種電気工事士学科試験の「単相交流回路」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「単相交流回路」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の三相交流回路の問題を解くための公式
- 第二種電気工事士学科試験の「三相交流回路」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「三相交流回路」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の消費電力量の問題を解くための公式
- 第二種電気工事士学科試験の「消費電力量」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「消費電力量」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の電力損失の問題を解くための公式
- 第二種電気工事士学科試験の「電力損失」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「電力損失」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の断線の問題を解くための公式
- 第二種電気工事士学科試験の「断線」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「断線」の計算問題の勉強や、試験直前の総復習などに活用してみてください。
- 第二種電気工事士学科試験の三相誘導電動機の問題を解くための公式
- 第二種電気工事士学科試験の「三相誘導電動機」の問題を解くために使う重要な公式とその使い方についてまとめています。第二種電気工事士学科試験の「三相誘導電動機」の計算問題の勉強や、試験直前の総復習などに活用してみてください。

