スポンサーリンク
火力発電所の効率
※ページ内にPR・広告が含まれる場合があります。
次の図のような火力発電所を考え、この火力発電所のボイラ効率、熱サイクル効率、タービン効率、タービン室効率、発電機効率、発電端熱効率、送電端熱効率、熱効率を求めてみます。
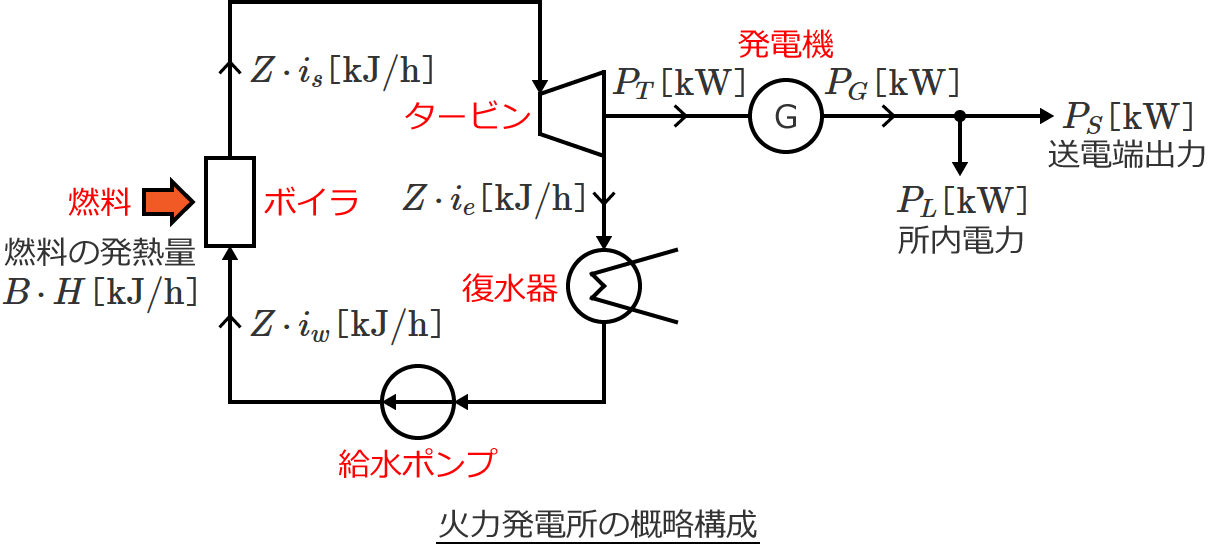
ここで、
$B$ :燃料消費量 [$ \mathrm{kg / h} $]
$H$ :燃料の発熱量 [$ \mathrm{kJ / kg} $]
$Z$ :蒸気・給水の流量 [$ \mathrm{kg / h} $]
$i_s$ :ボイラ出口蒸気のエンタルピー [$ \mathrm{kJ / kg} $]
$i_w$ :ボイラ入口給水のエンタルピー [$ \mathrm{kJ / kg} $]
$i_e$ :タービン排気のエンタルピー [$ \mathrm{kJ / kg} $]
$P_T$ :タービンの機械出力 [$ \mathrm{kW} $]
$P_G$ :発電機出力 [$ \mathrm{kW} $]
$P_L$ :所内電力 [$ \mathrm{kW} $]
$P_S$ :送電端出力 [$ \mathrm{kW} $]
です。
ちなみに、ボイラ式の火力発電は蒸気のエネルギーを利用した発電であるので、ボイラ式火力発電は汽力発電に分類されます。
スポンサーリンク
ボイラ効率
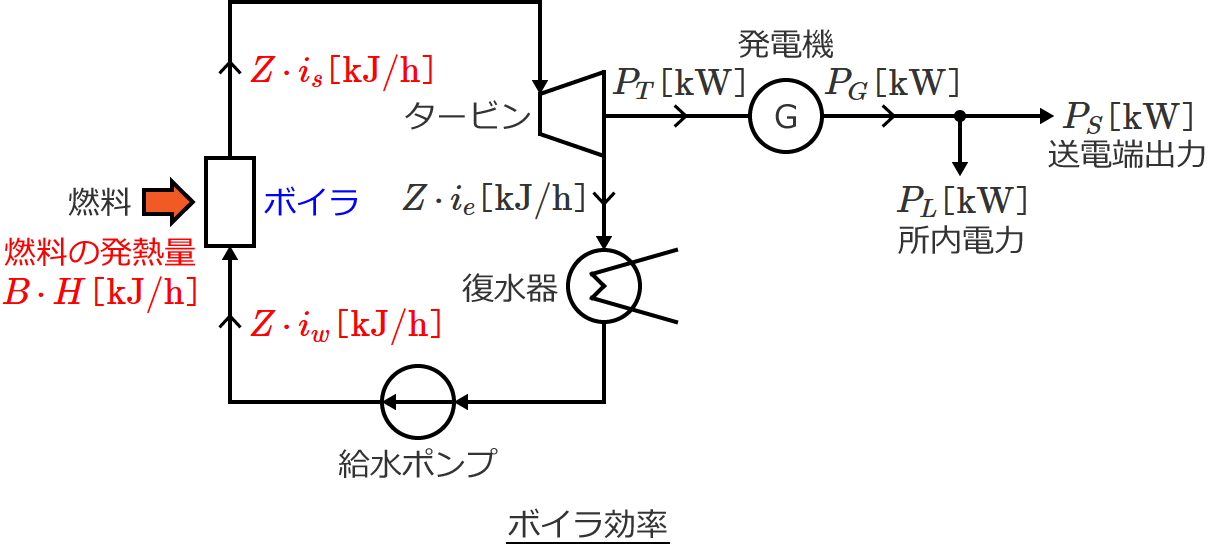
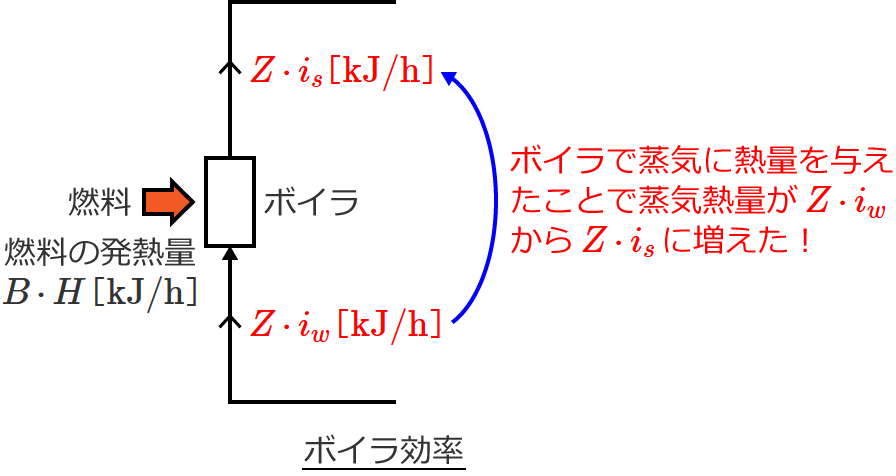
ボイラ効率 $\eta_B$ は、「ボイラに供給した燃料の発熱量」に対する「ボイラでの発生蒸気熱量」の比であるので、次式で与えられます。
$\eta_B = \dfrac{\text{ボイラでの発生蒸気熱量}}{\text{ボイラに供給した燃料の発熱量}}$ $= \dfrac{Z \, i_s - Z \, i_w}{BH}$
$\therefore \eta_B = \dfrac{Z ( i_s - i_w )}{BH}$
つまりボイラ効率 $\eta_B$ は、ボイラに供給した燃料の発熱量に対して、蒸気熱量がボイラでどれだけ増えたかという割合を表わしています。
熱サイクル効率
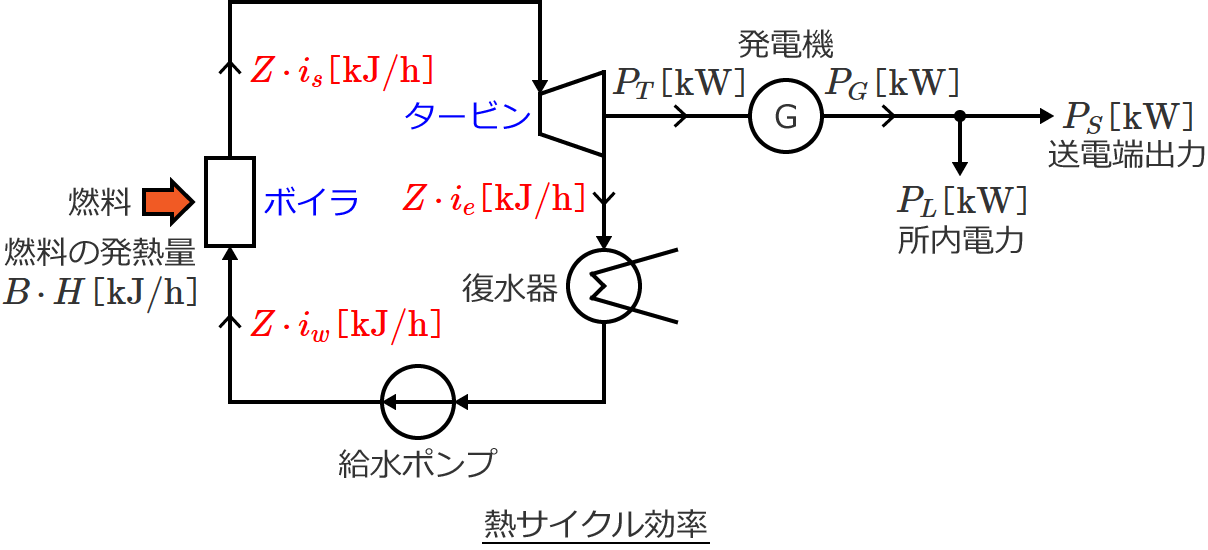
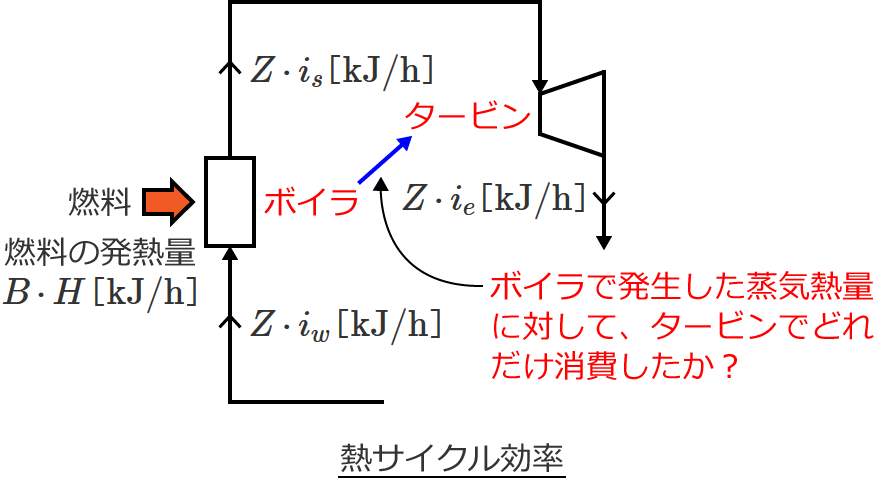
熱サイクル効率 $\eta_C$ は、「ボイラでの発生蒸気熱量」に対する「タービンで消費した熱量」の比であるので、次式で与えられます。
$\eta_C = \dfrac{\text{タービンで消費した熱量}}{\text{ボイラでの発生蒸気熱量}}$ $= \dfrac{Z \, i_s - Z \, i_e}{Z \, i_s - Z \, i_w}$ $= \dfrac{Z ( i_s - i_e )}{Z ( i_s - i_w )}$
$\therefore \eta_C = \dfrac{i_s - i_e}{i_s - i_w}$
つまり熱サイクル効率 $\eta_C$ は、ボイラで発生した蒸気熱量に対して、タービンでどれだけの熱量を消費したかという割合を表わしています。
スポンサーリンク
スポンサーリンク
タービン効率
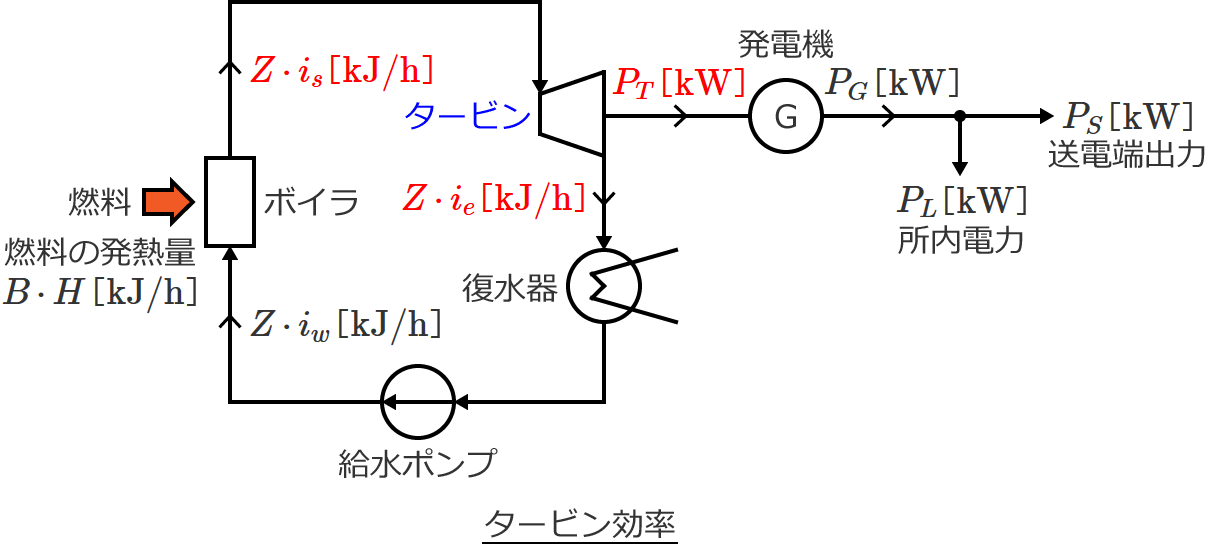
タービン効率 $\eta_T$ は、「タービンで消費した熱量」に対する「タービンの機械出力(熱量換算値)」の比であるので、次式で与えられます。
$\eta_T = \dfrac{\text{タービンの機械出力(熱量換算値)}}{\text{タービンで消費した熱量}}$ $= \dfrac{3600 P_T}{Z \, i_s - Z \, i_e}$
$\therefore \eta_T = \dfrac{3600 P_T}{Z ( i_s - i_e )}$
つまりタービン効率 $\eta_T$ は、タービンで消費した熱量がどれだけタービンの機械出力になったかという割合を表わしています。
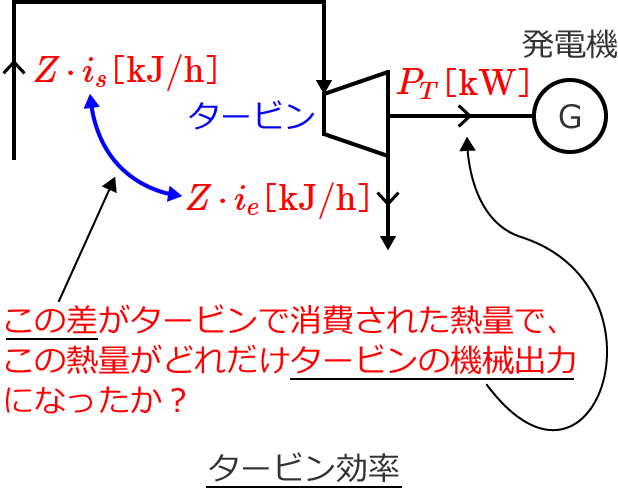
タービンの機械出力について
タービンの機械出力を $3600 \times P_T$($= 3600 P_T$)としていますが、これは出力の単位を $ \mathrm{kW} $ から $ \mathrm{kJ / h} $ に換算しているためです。(単位を熱量に合わせている。)
$1 \ \mathrm{W \cdot s} = 1 \ \mathrm{J}$
$1 \ \mathrm{W \cdot h} = 3600 \ \mathrm{J}$
$1 \ \mathrm{kW \cdot h} = 3600 \ \mathrm{kJ}$
$1 \ \mathrm{kW} = 3600 \ \mathrm{kJ / h}$
タービン室効率
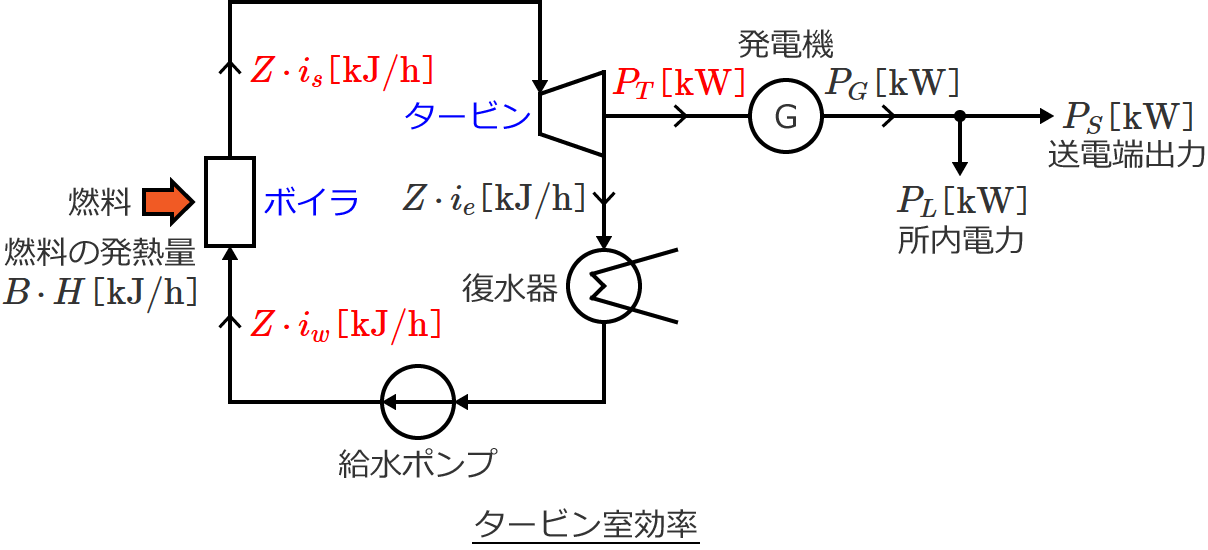
タービン室効率 $\eta_{TR}$ は、「ボイラでの発生蒸気熱量」に対する「タービンの機械出力(熱量換算値)」の比であるので、次式で与えられます。
$\eta_{TR} = \dfrac{\text{タービンの機械出力(熱量換算値)}}{\text{ボイラでの発生蒸気熱量}}$ $= \dfrac{3600 P_T}{Z \, i_s - Z \, i_w}$
$\therefore \eta_{TR} = \dfrac{3600 P_T}{Z ( i_s - i_w )}$
つまりタービン室効率 $\eta_{TR}$ は、ボイラで発生した蒸気熱量に対して、タービンの機械出力はどれだけかという割合を表わしています。
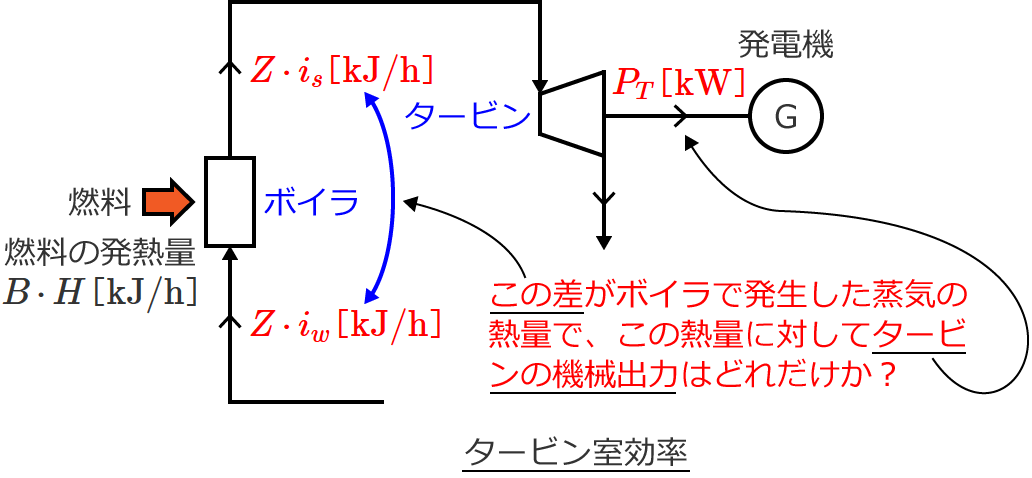
タービン効率とタービン室効率の違い
タービン効率とタービン室効率は違うものなので注意してください。
タービン効率とは、「タービンで消費した熱量」に対する「タービンの機械出力」の比
タービン室効率とは、「ボイラでの発生蒸気熱量」に対する「タービンの機械出力」の比
タービンの機械出力について
ここでのタービンの機械出力も、熱量に換算した値($= 3600 P_T$)です。
発電機効率
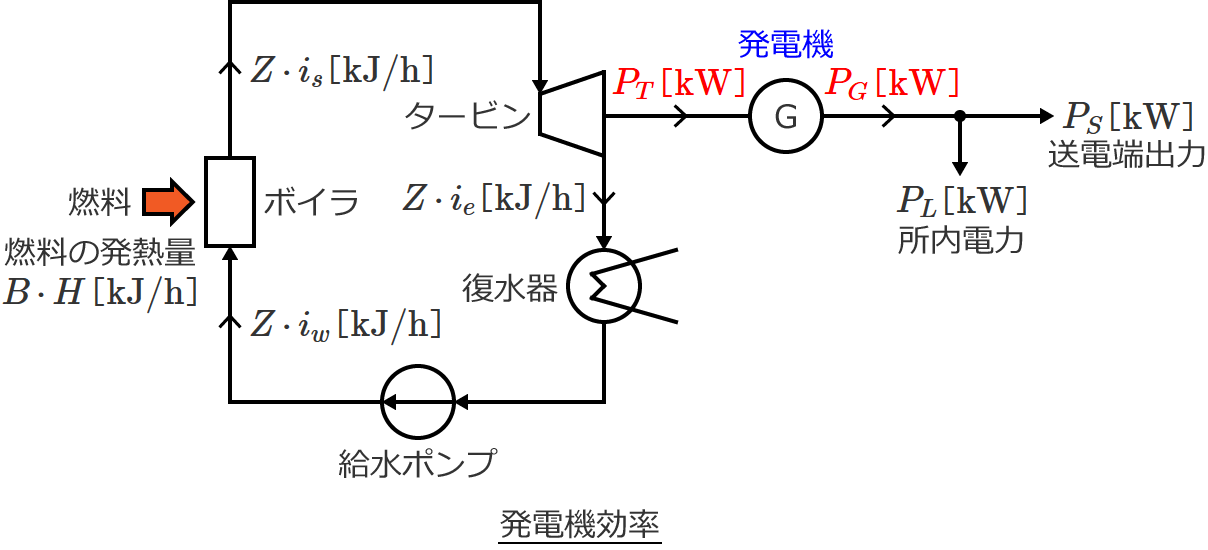
発電機効率 $\eta_G$ は、「タービンの出力(=発電機の入力)」に対する「発電機の出力」の比であるので、次式で与えられます。
$\eta_G = \dfrac{\text{発電機の出力}}{\text{タービンの出力}} = \dfrac{P_G}{P_T}$
$\therefore \eta_G =\dfrac{P_G}{P_T}$
つまり発電機効率 $\eta_G$ は、発電機への入力に対して、発電機の出力はどれだけかという割合を表わしています。
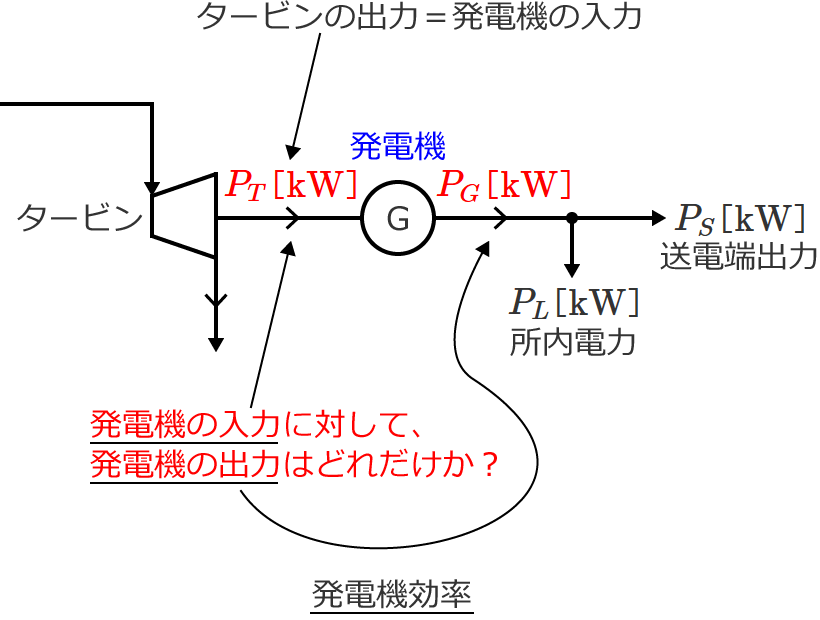
発電機の入力について
タービンの出力がそのまま発電機に入力されるので、「タービンの出力=発電機の入力」になります。
発電端熱効率
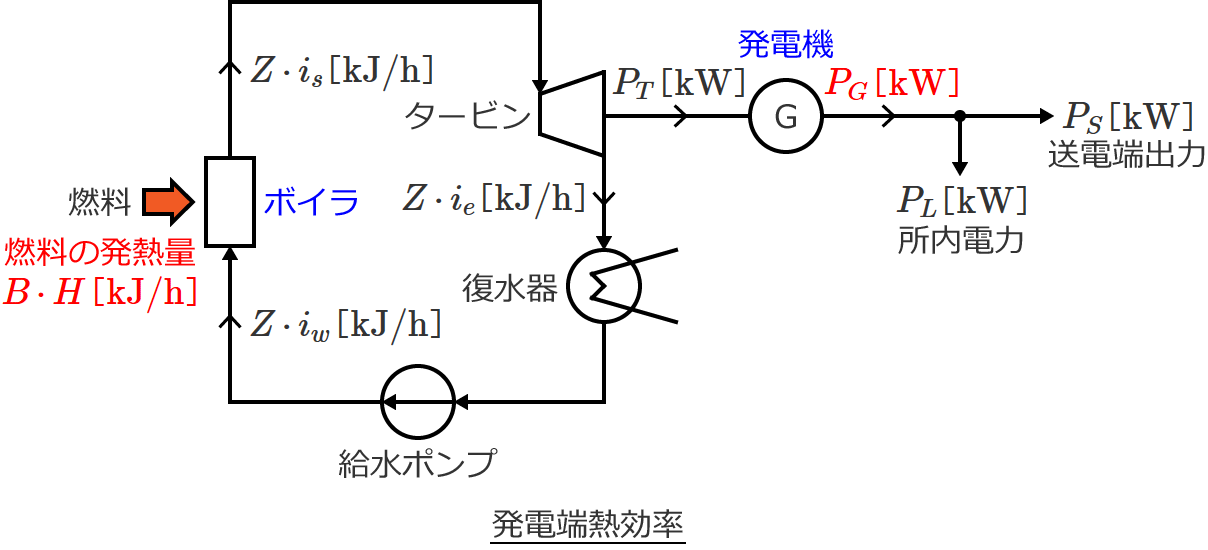
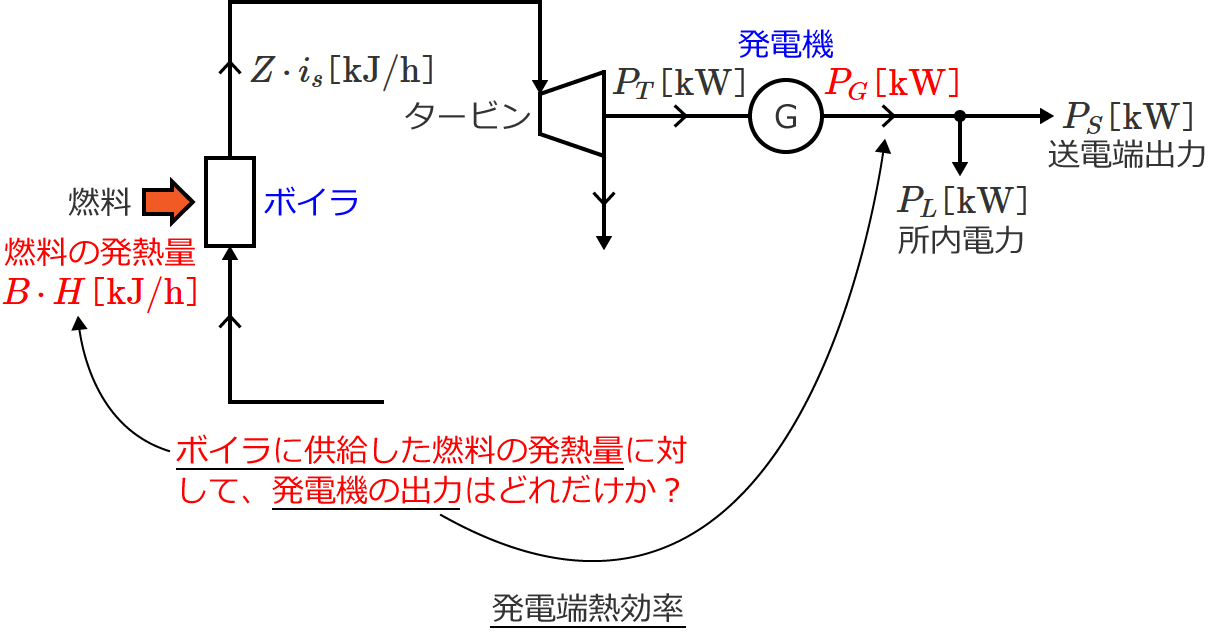
発電端熱効率 $\eta_P$ は、「ボイラに供給した燃料の発熱量」に対する「発電機出力(熱量換算値)」の比であるので、次式で与えられます。
$\eta_P = \dfrac{\text{発電機出力(熱量換算値)}}{\text{ボイラに供給した燃料の発熱量}}$ $= \dfrac{3600 P_G}{BH}$
$\therefore \eta_P = \dfrac{3600 P_G}{BH}$
つまり発電端熱効率 $\eta_P$ は、ボイラに供給した燃料の発熱量に対して、発電機の出力はどれだけかという割合を表わしています。
発電機出力について
ここでの発電機出力も、熱量に換算した値($= 3600 P_G$)です。
送電端熱効率
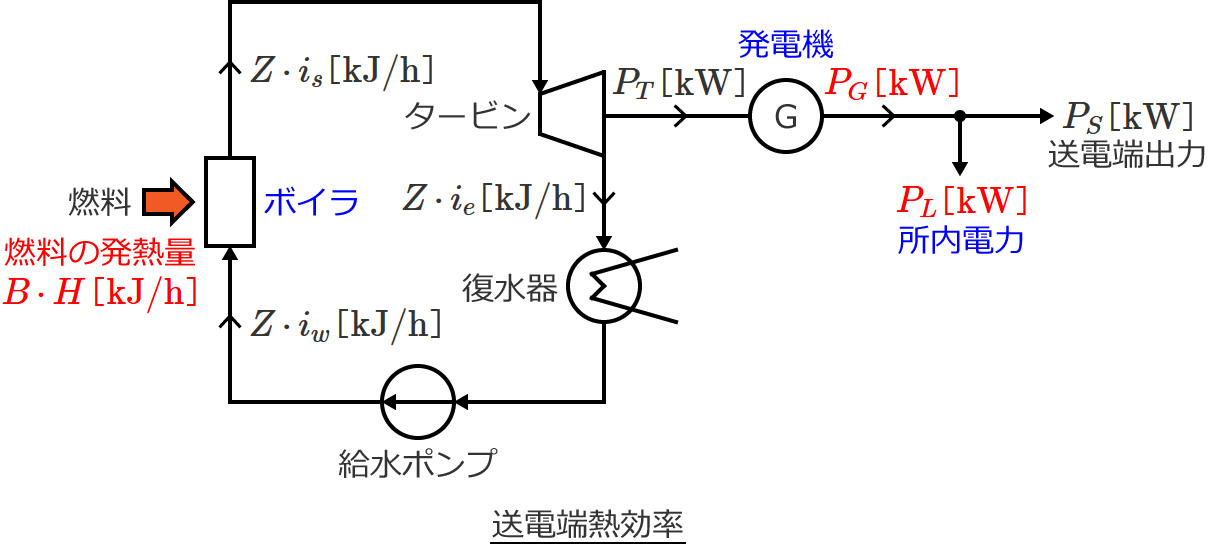
送電端熱効率 $\eta_S$ は、「ボイラに供給した燃料の発熱量」に対する「送電端出力」の比であるので、次式で与えられます。
$\eta_S = \dfrac{\text{送電端出力}}{\text{ボイラに供給した燃料の発熱量}}$ $= \dfrac{\text{発電機出力(熱量換算値)} - \text{所内電力(熱量換算値)}}{\text{ボイラに供給した燃料の発熱量}}$
$= \dfrac{3600 P_G - 3600 P_L}{BH}$
$\therefore \eta_S = \dfrac{3600 ( P_G - P_L )}{BH}$
つまり送電端熱効率 $\eta_S$ は、ボイラに供給した燃料の発熱量に対して、送電端での出力はどれだけかという割合を表わしています。
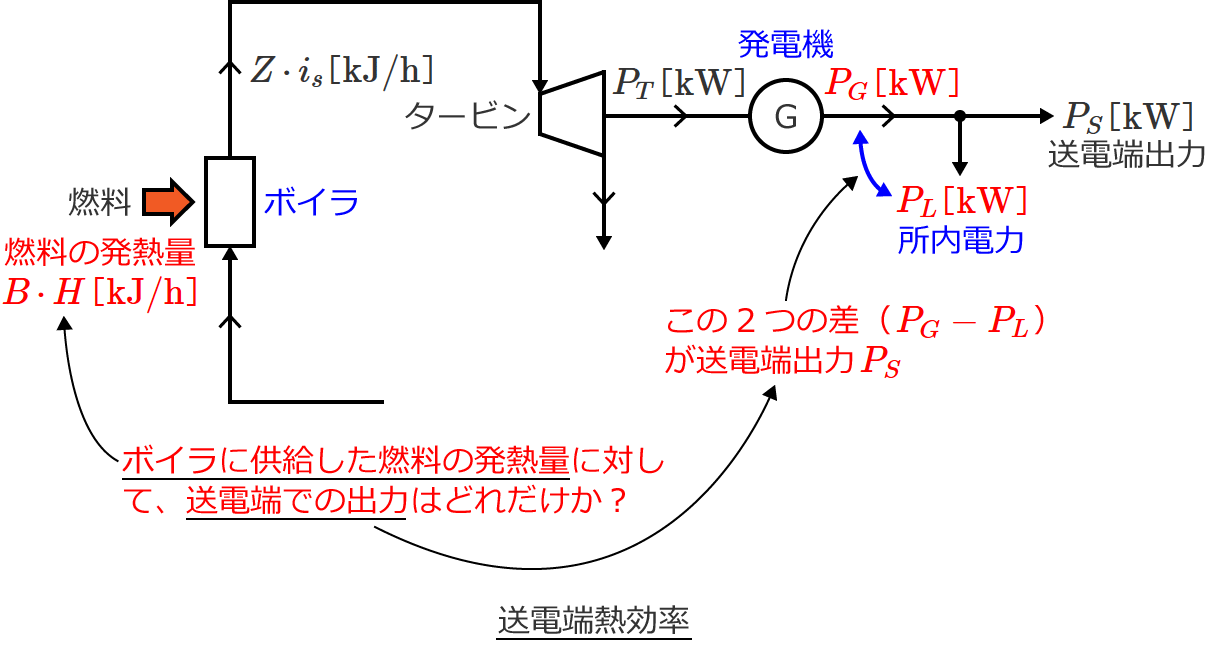
ここで送電端出力は発電所から送電される電力であるので、送電端出力は「発電機で発電した電力(発電機出力)」から「発電所内で使用する電力(所内電力)」を引いたものになります。
発電機出力と所内電力について
ここでの発電機出力と所内電力も、熱量に換算した値($3600 P_G$ および $3600 P_L$)です。
熱効率
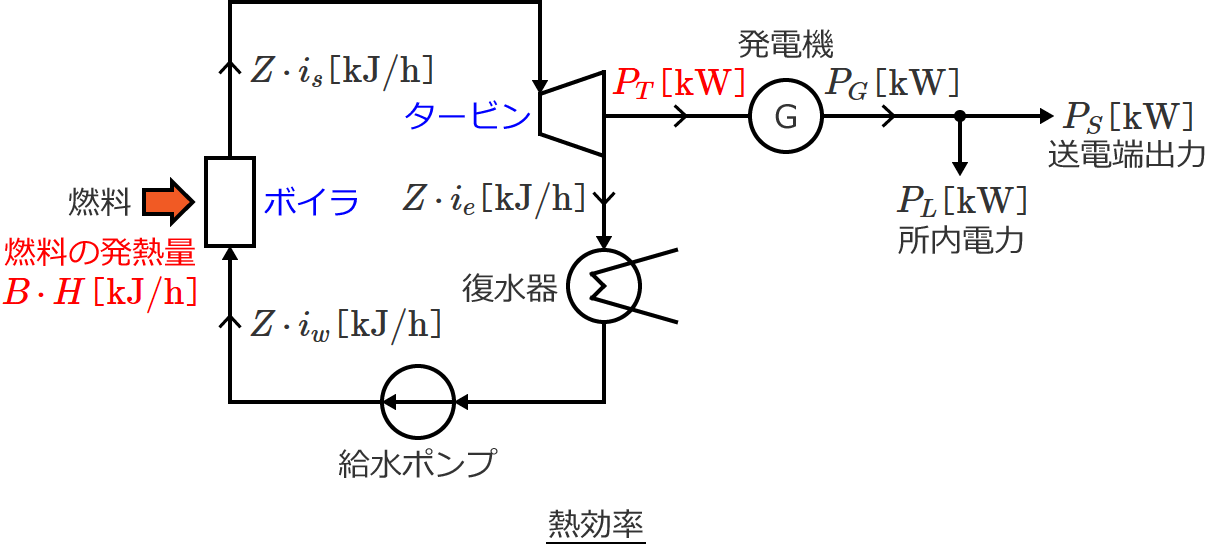
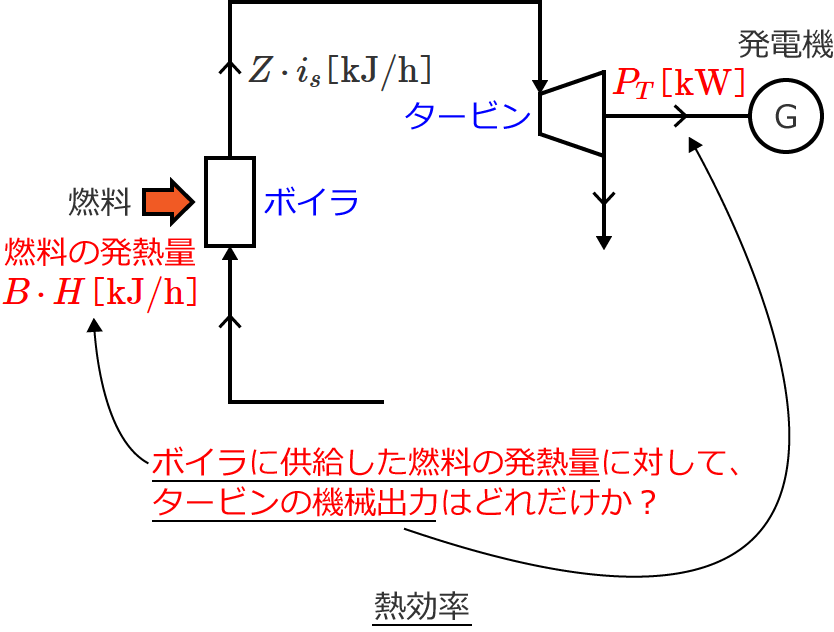
熱効率 $\eta$ は、「ボイラに供給した燃料の発熱量」に対する「タービンの機械出力(熱量換算値)」の比であるので、次式で与えられます。
$\eta = \dfrac{\text{タービンの機械出力(熱量換算値)}}{\text{ボイラに供給した燃料の発熱量}}$ $= \dfrac{3600 P_T}{BH}$
$\therefore \eta = \dfrac{3600 P_T}{BH}$
つまり熱効率 $\eta$ は、ボイラに供給した燃料の発熱量に対して、タービンの機械出力はどれだけかという割合を表わしています。
タービンの機械出力について
ここでのタービンの機械出力も、熱量に換算した値($= 3600 P_T$)です。
火力発電所の効率のまとめ表
火力発電所のボイラ効率、熱サイクル効率、タービン効率、タービン室効率、発電機効率、発電端熱効率、送電端熱効率、熱効率の式を一覧表にまとめると次の表のようになります。
| 効率の種類 | 効率の式 |
|---|---|
| ボイラ効率 | $\eta_B = \dfrac{Z ( i_s - i_w )}{BH}$ |
| 熱サイクル効率 | $\eta_C = \dfrac{i_s - i_e}{i_s - i_w}$ |
| タービン効率 | $\eta_T = \dfrac{3600 P_T}{Z ( i_s - i_e )}$ |
| タービン室効率 | $\eta_{TR} = \dfrac{3600 P_T}{Z ( i_s - i_w )}$ |
| 発電機効率 | $\eta_G =\dfrac{P_G}{P_T}$ |
| 発電端熱効率 | $\eta_P = \dfrac{3600 P_G}{BH}$ |
| 送電端熱効率 | $\eta_S = \dfrac{3600 ( P_G - P_L )}{BH}$ |
| 熱効率 | $\eta = \dfrac{3600 P_T}{BH}$ |
スポンサーリンク
スポンサーリンク
火力発電所の損失と出力 ←BACK
NEXT→ タービン室効率
スポンサーリンク
火力発電所の効率 関連ページ
- 火力発電の概要
- 火力発電の「火力発電の概要」についてまとめたページです。「火力発電の概要」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 火力発電所の損失と出力
- 火力発電の「火力発電所の損失と出力」についてまとめたページです。「火力発電所の損失と出力」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- タービン室効率
- 火力発電の「タービン室効率」についてまとめたページです。「タービン室効率」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 復水器で海水へ放出される熱量
- 火力発電の「復水器で海水へ放出される熱量」についてまとめたページです。「復水器で海水へ放出される熱量」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 電力量と熱量の関係(換算)
- 火力発電の「電力量」についてまとめたページです。「電力量」は第三種電気主任技術者試験(電験三種)でも出題される項目です。
- 熱消費率
- 火力発電の「熱消費率」についてまとめたページです。「熱消費率」は第三種電気主任技術者試験(電験三種)でも出題される項目です。


