スポンサーリンク
積分の公式
※ページ内にPR・広告が含まれる場合があります。
積分の公式をまとめてみました。
積分の公式も微分の公式と同じように、あれもこれもと並べると数多くあり、すべての公式をおぼえるのは大変です。
なので、このページでも微分の公式のページと同じように電気数学で「よく使う積分の公式」、「ほとんど使わない積分の公式」※に分けてみました。
※個人的な公式の使用頻度で分けていますので、人によっては「それは使わないなぁ〜」とか、「これはよく使う」とかあると思いますが、それはそれで・・・。
「ほとんど使わない積分の公式」はおぼえる必要はなく(暗記しなくてもいいんじゃない、という意味)、必要なときに調べて使えばいいと思いますが、「よく使う積分の公式」はおぼえておくようにしましょう。
また、微分と積分には、
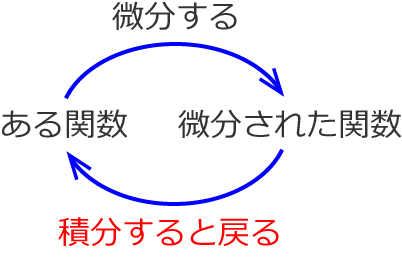
という関係があるので、微分の公式と積分の公式をセットで勉強すると効率的におぼえることができます。
それからちょっと補足ですが、このページに書いてある式の意味は、積分記号の中の式を積分すると右辺の式になります、という意味です。

スポンサーリンク
よく使う積分の公式
● $\displaystyle\int 1\, dx=x+C$ ※「$1$」を積分すると $x$
● $\displaystyle\int a\, dx=a\, x+C$ ($a$ は定数)
● $\displaystyle\int x^n\, dx=\dfrac{1}{n+1} x^{n+1}+C$ $\left( n\neq -1\right)$ ※基本中の基本!
● $\displaystyle\int\dfrac{1}{x}\, dx =\log_e |x|+C$
● $\displaystyle\int\dfrac{1}{x\pm a}\, dx=\log_e |x\pm a|+C$ ($a$ は定数)
● $\displaystyle\int a^x\, dx=\dfrac{a^x}{\log_e a} +C$ $\left( a\gt 0\ ,\ a\neq 1\right)$
● $\displaystyle\int e^{ax}\, dx=\dfrac{1}{a} e^{ax}+C$ ($a$ は定数)
● $\displaystyle\int\sin x\, dx=-\cos x+C$ ※基本中の基本!
● $\displaystyle\int\cos x\, dx=\sin x+C$ ※基本中の基本!
● $\displaystyle\int\sin ax\, dx=-\dfrac{1}{a}\cos ax+C$ ($a$ は定数)
● $\displaystyle\int\cos ax\, dx=\dfrac{1}{a}\sin ax+C$ ($a$ は定数)
※$C$ は積分定数です。
ほとんど使わない積分の公式
● $\displaystyle\int \log_e x\, dx=x\left(\log_e x-1\right) +C$
● $\displaystyle\int a^{bx}\, dx=\dfrac{a^{bx}}{b\log_e a} +C$ $\left( a\gt 0\ ,\ a\neq 1\right)$
● $\displaystyle\int x\, e^{ax}\, dx=\dfrac{e^{ax}}{a^2}\left( ax-1\right) +C$ ($a$ は定数)
● $\displaystyle\int \tan x\, dx=-\log_e |\cos x|+C$
● $\displaystyle\int \cot x\, dx=\log_e |\sin x|+C$
● $\displaystyle\int\dfrac{1}{\sin x}\, dx=\log_e \left|\tan\dfrac{x}{2}\right|+C$
● $\displaystyle\int\dfrac{1}{\cos x}\, dx$ $=\log_e\left|\tan\left(\dfrac{\pi}{4} +\dfrac{x}{2}\right)\right| +C$
● $\displaystyle\int\sin^2 x\, dx=\dfrac{1}{2} x-\dfrac{1}{4}\sin 2x+C$
● $\displaystyle\int\cos^2 x\, dx=\dfrac{1}{2} x+\dfrac{1}{4}\sin 2x+C$
● $\displaystyle\int\sin^{-1} x\, dx$ $=x\sin^{-1} x+\sqrt{1-x^2} +C$
● $\displaystyle\int\cos^{-1} x\, dx$ $=x\cos^{-1} x-\sqrt{1-x^2} +C$
● $\displaystyle\int\mathrm{cosec}^2 ax\, dx=-\dfrac{1}{a}\cot ax+C$ ($a$ は定数)
● $\displaystyle\int\sec^2 ax\, dx=\dfrac{1}{a}\tan ax+C$ ($a$ は定数)
● $\displaystyle\int\sinh x\, dx=\cosh x+C$
● $\displaystyle\int\cosh x\, dx=\sinh x+C$
● $\displaystyle\int\tanh x\, dx=\log_e\cosh x+C$
● $\displaystyle\int\dfrac{1}{\sqrt{a^2-x^2}}\, dx=\sin^{-1}\dfrac{x}{|a|}+C$ ($a$ は定数)
● $\displaystyle\int\dfrac{1}{a^2+x^2}\, dx=\dfrac{1}{a}\tan^{-1}\dfrac{x}{a}+C$ ($a$ は定数)
● $\displaystyle\int\dfrac{1}{\sqrt{x^2\pm a^2}}\, dx$ $=\log_e \left| x+\sqrt{x^2\pm a^2}\right| +C$ ($a$ は定数)
● $\displaystyle\int\sqrt{a^2-x^2}\, dx$ $=\dfrac{1}{2}\left( x\sqrt{a^2-x^2} +a^2\sin^{-1}\dfrac{x}{|a|}\right) +C$ ($a$ は定数)
● $\displaystyle\int\sqrt{x^2\pm a^2}\, dx$ $=\dfrac{1}{2}\left( x\sqrt{x^2\pm a^2}\pm a^2\log_e\left| x+\sqrt{x^2\pm a^2}\right|\right) +C$ ($a$ は定数)
● $\displaystyle\int\dfrac{1}{x^2-a^2}\, dx$ $=\dfrac{1}{2a}\log_e\left|\dfrac{x-a}{x+a}\right| +C$ ($a$ は定数)
※$C$ は積分定数です。
スポンサーリンク
スポンサーリンク
電気数学のお勉強 ←BACK
NEXT→ 部分積分の公式の導出
スポンサーリンク
積分の公式 関連ページ
- 部分積分の公式の導出
- 部分積分の公式を導出してみました。部分積分の公式は積の微分の公式から導出できます。


