電気数学のお勉強｜計算の基礎｜最小の定理

スポンサーリンク

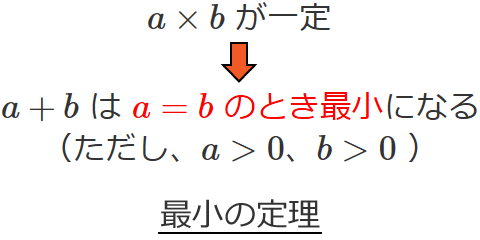
2つの正の数 $a$、$b$ の積（ $a\times b$ ）が一定ならば、それら2つの数の和 $a+b$ は、$a=b$ のときに最小になります。これを、最小の定理（または最小定理）といいます。

 

 

最小の定理は、例えば、

 

「 $x\gt 0$ のとき、$\dfrac{4}{x} +x$ の最小値は？」

 

というように、2つの正の数が和の形になっているときの最小値を求めるときに使えます。（ただし最小の定理を使うためには、2つの数が正という条件の他に、2つの数の積が一定（定数）になるという条件が必要です。）

 

 

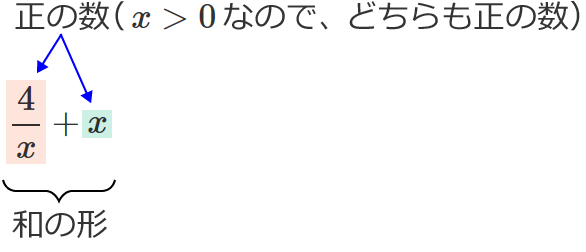
最小の定理を使って、$\dfrac{4}{x} +x$（ただし、$x\gt 0$ ）の最小値を求めてみると次のようになります。

 

まず初めに、最小の定理を使えるかどうかを確認します。

 

$x\gt 0$（ $x$ は正）なので、2つの数 $\dfrac{4}{x}$ と $x$ はどちらも正の数になります。…①

 

また、2つの数の積を求めると、

 

$\dfrac{4}{x}\times x =4$　（2つの数の積）

 

となり、2つの数の積は一定の値（定数）になります。…②

 

したがって①、②より、この場合は最小の定理を使えます。

 

最小の定理より、2つの数の和 $\dfrac{4}{x} +x$ は $\dfrac{4}{x} =x$ のときに最小になるので、これより $x$ の値を求めると、

 

$\dfrac{4}{x} =x$

 

$x^2=4$

 

$x=\pm\sqrt{4} =\pm 2$

 

となりますが、$x\gt 0$ なので、

 

$\therefore x=2$　（$\dfrac{4}{x} +x$ が最小になるときの $x$ の値）

 

となります。あとはこの $x=2$ を $\dfrac{4}{x} +x$ に代入するだけです。

 

$\dfrac{4}{x} +x=\dfrac{4}{2} +2$　（$x=2$ を代入した）

 

$=2+2=4$

 

 

となり、$\dfrac{4}{x} +x$ の最小値が求められました。

 

このように、最小の定理を使うと、2つの正の数が和の形になっている式の最小値を求めることができます。（ただし、2つの正の数の積が一定（定数）になるという条件が必要。）

 

 

最小の定理の証明

最小の定理は、次のように証明できます。

 

まず、$a$、$b$ を正の数とし、$a$ と $b$ との積 $ab$ は一定の値になるものとします。

 

このとき、2つの正の数 $a$、$b$ の和 $a+b$ は、

 

$a+b=\left(\sqrt{\mathstrut a}\right)^2 +\left(\sqrt{\mathstrut b}\right)^2$

 

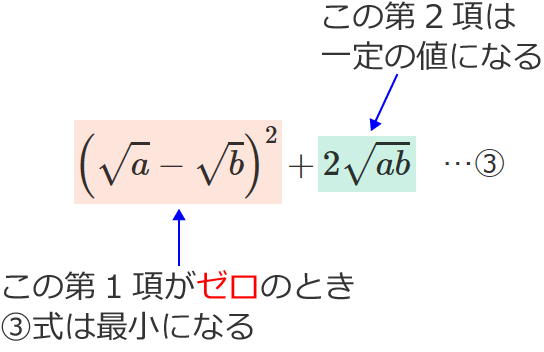
$=\left(\sqrt{\mathstrut a} -\sqrt{\mathstrut b}\right)^2+2\sqrt{\mathstrut a \mathstrut b}$　…③　（$\because \left(\sqrt{\mathstrut a} -\sqrt{\mathstrut b}\right)^2$ $=\left(\sqrt{\mathstrut a}\right)^2 -2\sqrt{\mathstrut a \mathstrut b} +\left(\sqrt{\mathstrut b}\right)^2$ ）

 

と変形できます。この③式において、$a$ と $b$ との積 $ab$ は一定の値なので、$2\sqrt{\mathstrut a \mathstrut b}$ も一定の値になります。したがって、③式の第1項がゼロのときに③式は最小になります。

 

 

③式の第1項 $=0$ とすると、

 

$\left(\sqrt{\mathstrut a} -\sqrt{\mathstrut b}\right)^2 =0$

 

$\sqrt{\mathstrut a} -\sqrt{\mathstrut b} =0$

 

$\sqrt{\mathstrut a} =\sqrt{\mathstrut b}$

 

 

となるので、$a=b$ のときに③式（つまり、$a+b$ ）が最小になることになります。（証明終わり）

 

ちなみに、$a=b$ のときに $a+b$ が最小になるので、$a+b$ の最小値は $2\sqrt{\mathstrut a \mathstrut b}$（ $=2a$ または $2b$ ）になります。

 

 

関数の最大・最小を求めるときには一般に微分を使って求めますが、最小の定理を使える場合には、最小の定理を使うと簡単に最小値を求めることができます。また、最小の定理を使うと計算時間も短縮されますので、最小の定理はおぼえておくようにしましょう。

 

 

 

最小の定理は最小値を求めるときに使える定理ですが、分数で表わされた式の最大値を求めるときにも使われることがあります。
こちらの電源から供給できる最大電力（最大有能電力）のページでは、最小の定理を使って電圧源から供給できる最大電力を求めていますので、こちらのページも最小の定理の使い方の参考にしてみてください。

 

最大値を求めるときに使える最大の定理については、こちらの最大の定理のページを参考にしてみてください。

電気数学のお勉強　←BACK

NEXT→　最大の定理

スポンサーリンク

最小の定理　関連ページ

最大の定理

最大の定理について解説しています。最大の定理の証明などについても解説していますので参考にしてみてください。