電気数学のお勉強｜計算の基礎｜最大の定理

スポンサーリンク

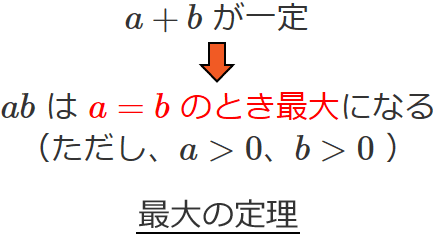
2つの正の数 $a$、$b$ の和（ $a+b$ ）が一定ならば、それら2つの数の積 $ab$ は、$a=b$ のときに最大になります。これを、最大の定理といいます。

 

 

最大の定理の証明

最大の定理は、次のように証明できます。

 

まず、$a$、$b$ を正の数とし、$a$ と $b$ との和 $a+b$ は、$a+b=k$ 一定（定数）になるものとします。

 

このとき、2つの正の数 $a$、$b$ の積 $ab$ は、

 

$ab=a\times\left( k-a\right)$　（$b=k-a$ を代入した（ $\because a+b=k$ ））

 

$=ak-a^2$

 

$=-\left( a^2-ka\right)$

 

$=-\left( a-\dfrac{k}{2}\right)^2+\dfrac{k^2}{4}$　…①　（$\because -\left( a-\dfrac{k}{2}\right)^2 =-a^2+ka-\dfrac{k^2}{4}$ ）

 

と表わせます。この①式は上に凸の2次関数で、$a=\dfrac{k}{2}$ のときに最大になります。

 

このときの $b$ の値を求めてみると、$b$ の値は $b=k-a$ より、

 

$b=k-a$

 

$=k-\dfrac{k}{2}$　（$a=\dfrac{k}{2}$ を代入した）

 

$=\dfrac{k}{2}$

 

となるので、$a=\dfrac{k}{2}$ のとき $b$ は $a$ と等しい値 $b=\dfrac{k}{2}$ になります。

 

したがって、①式（つまり、$ab$ ）は、$a=b$ のときに最大になることになります。（証明終わり）

 

 

 

最大の定理は最大値を求めるときに使える定理ですが、最小値を求めるときに使える最小の定理もあります。最小の定理については、こちらの最小の定理のページを参考にしてみてください。

最小の定理　←BACK

NEXT→　電気数学のお勉強

スポンサーリンク

最大の定理　関連ページ

最小の定理

最小の定理（最小定理）について解説しています。最小の定理の使い方や、最小の定理の証明などについても解説していますので参考にしてみてください。