スポンサーリンク
配電線の電圧降下
※ページ内にPR･広告が含まれる場合があります。
配電線路の計算をするときに、電線路の電圧降下を考える場合があります。
ところで、電線路の電圧降下ってなんでしょうか？
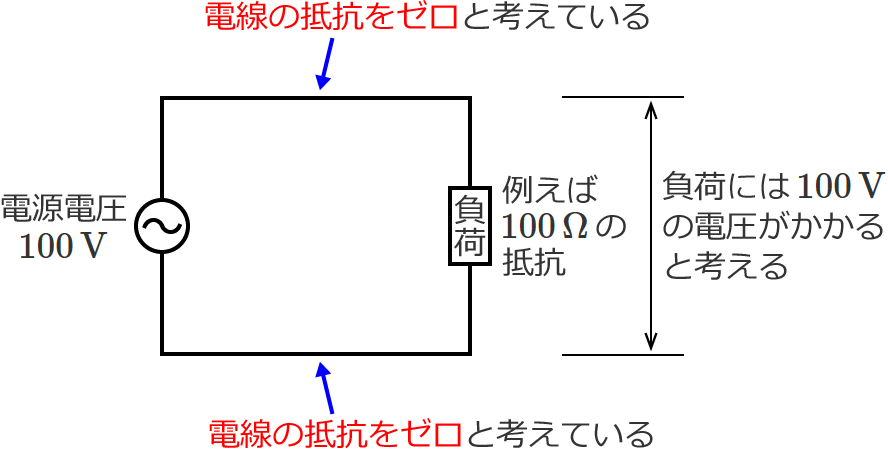
例えば、次のような電気回路で「負荷にかかる電圧は？」という場合、「$100\,\mathrm{V}$ の電圧がかかる」と考えますよね？
これは、電源と負荷をつなぐ電線の抵抗をゼロ（ゼロオーム）と考えているので、このように考えているわけです。
ですが、電源と負荷をつなぐ電線の抵抗を考えた場合にはどうでしょうか？
回路図で書いてみると、次のような回路になります。
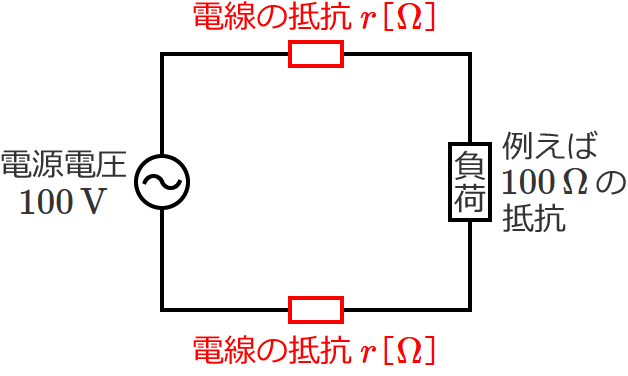
この場合、電源の電圧 $100\,\mathrm{V}$ が「電線の抵抗」と「$100\,\Omega$ の抵抗負荷」に分圧されるため、$100\,\Omega$ の抵抗負荷にかかる電圧は、
電源の 100V よりも小さくなります。
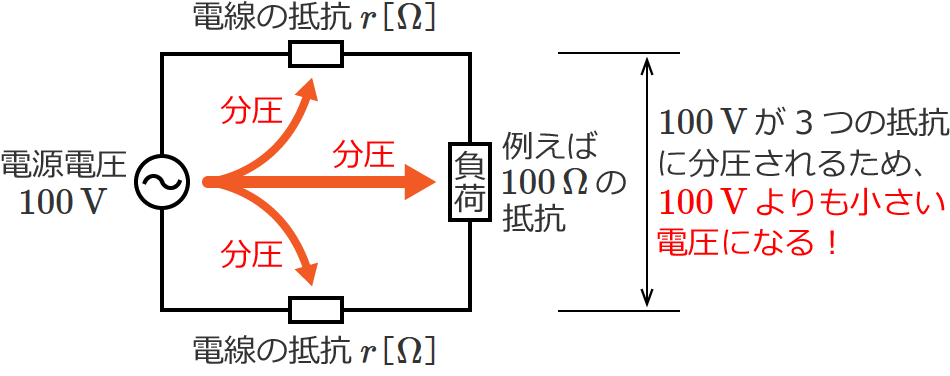
このように、電源の電圧が電線の抵抗にもかかり、電源の電圧よりも負荷にかかる電圧が小さくなっていることを電圧降下が生じているといったりします。
それから、単に電圧降下という場合には、
負荷にかかる電圧が電線の抵抗によって小さくなった分の電圧
または、
電線の抵抗にかかる電圧そのもの
をいったりします。
では、もうちょっと具体的に数字で考えてみます。
例えば、電線1本の抵抗にかかる電圧を $5\,\mathrm{V}$ とすると、単相2線式では、電線は「電源から負荷まで」と「負荷から電源まで」の往復の2本あるので、2本の電線の抵抗にかかる電圧は合計で $10\,\mathrm{V}$ になります。
すると、「電源電圧 $100\,\mathrm{V}$」から「2本の電線の抵抗にかかる電圧 $10\,\mathrm{V}$」を引いた電圧が抵抗負荷にかかるので、抵抗負荷には $90\,\mathrm{V}$ の電圧がかかることになります。
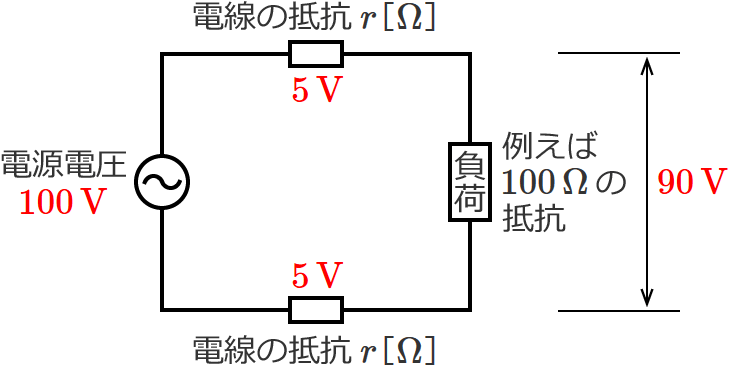
負荷の電圧 $=$ 電源電圧 $100\,\mathrm{V}$ $-$ 2本の電線の抵抗にかかる電圧 $10\,\mathrm{V}$ $=90\,\mathrm{V}$
（電源電圧 $100\,\mathrm{V}$ よりも $10\,\mathrm{V}$ 小さくなる。）
なので、この場合の電圧降下は $10\,\mathrm{V}$ ということになります。
それでは次に、配電方式ごとの電圧降下を求めてみましょう。
スポンサーリンク
単相2線式配電線の電圧降下
単相2線式配電線の回路は、次のようになります。（負荷は抵抗負荷とします。）
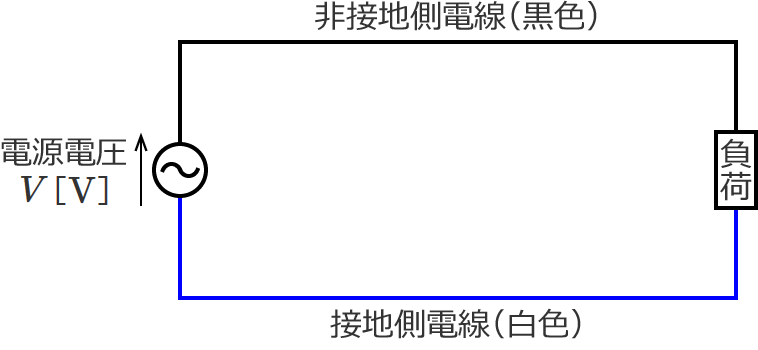
この単相2線式回路の電線1本の抵抗を $r$［$\Omega$］とし、電流 $I$［$\mathrm{A}$］の流れも書くと次のようになります。
この場合、電圧降下はいくらでしょうか？
上の回路図より電線の抵抗 $r$［$\Omega$］には $I$［$\mathrm{A}$］の電流が流れているので、1本の電線の抵抗にかかる電圧はオームの法則より $Ir$［$\mathrm{V}$］になります。
この $Ir$［$\mathrm{V}$］が電線1本あたりの電圧降下の大きさになるので、単相2線式回路の電線2本分（「電源から負荷まで」と「負荷から電源まで」の往復2本分）の電圧降下は、
電圧降下 $=2\times Ir =2Ir$
$\therefore$ 電圧降下 $=2Ir$ ［$\mathrm{V}$］
となります。
スポンサーリンク
スポンサーリンク
単相3線式配電線の電圧降下
単相3線式配電線の回路は、次のようになります。（負荷は抵抗負荷とします。）
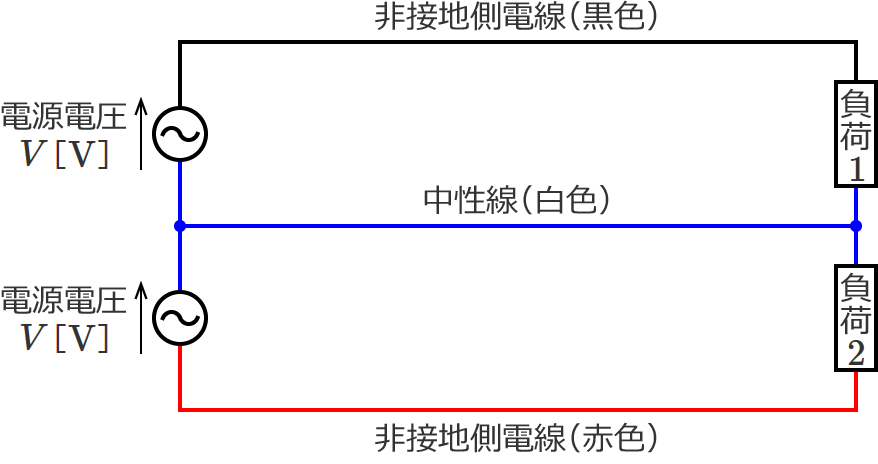
単相3線式回路の場合、負荷によって中性線に流れる電流の大きさや向きが変わるため、次の3つに分けて電圧降下を考えてみます。
- 中性線の電流がゼロの場合
- 中性線に左向きの電流が流れる場合
- 中性線に右向きの電流が流れる場合
中性線の電流がゼロの場合
中性線の電流がゼロの場合というのは、負荷1と負荷2に流れる電流が等しくなる場合で、単相3線式回路の電線1本の抵抗を $r$［$\Omega$］とし、電流の流れも書くと次のようになります。
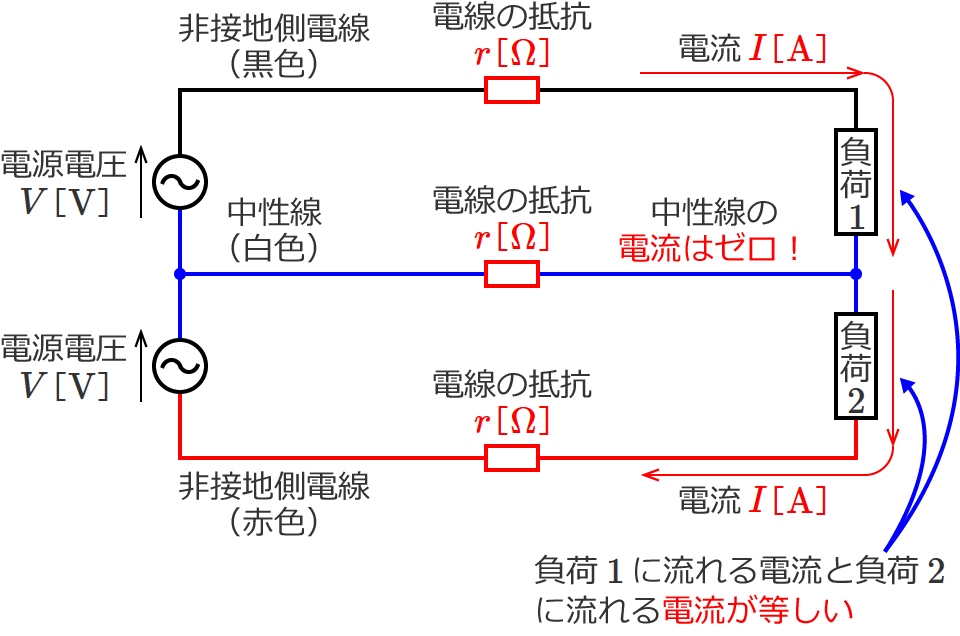
この場合、中性線の電流がゼロなので、負荷1側（上側）の電圧降下も、負荷2側（下側）の電圧降下も、どちらも、
$\therefore$ 電圧降下 $=Ir$ ［$\mathrm{V}$］
になります。
中性線に左向きの電流が流れる場合
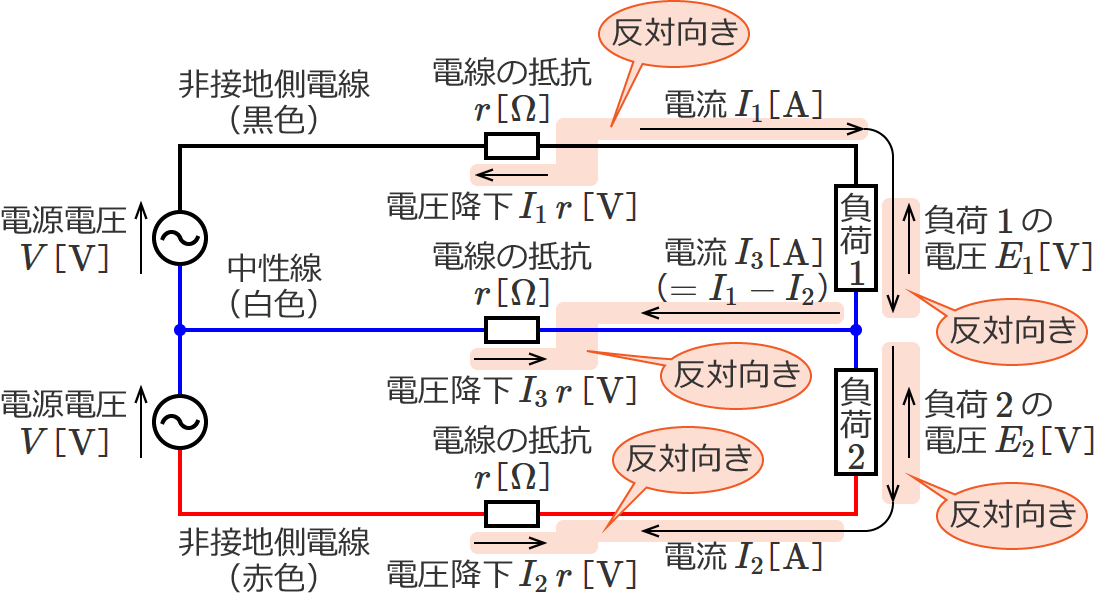
中性線に左向きの電流が流れる場合というのは、次の図で電流 $I_1$［$\mathrm{A}$］が電流 $I_2$［$\mathrm{A}$］よりも大きい場合です。このとき、$I_1$ から $I_2$ を引いた大きさの電流（図の $I_3$（$=I_1-I_2$））が左向きに流れます。
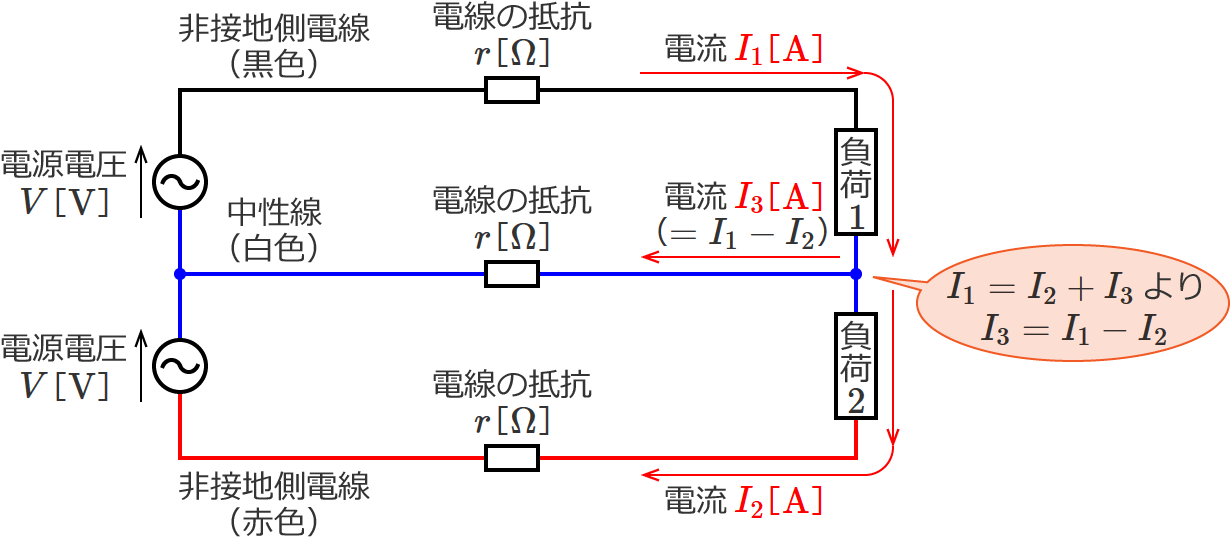
この場合の各電線の抵抗における電圧降下は、次のようになります。
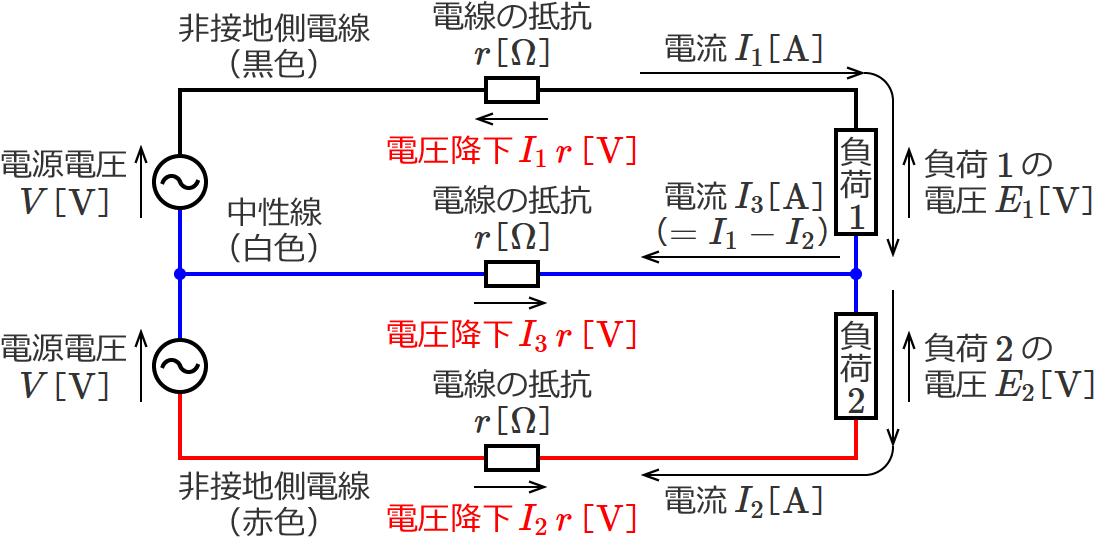
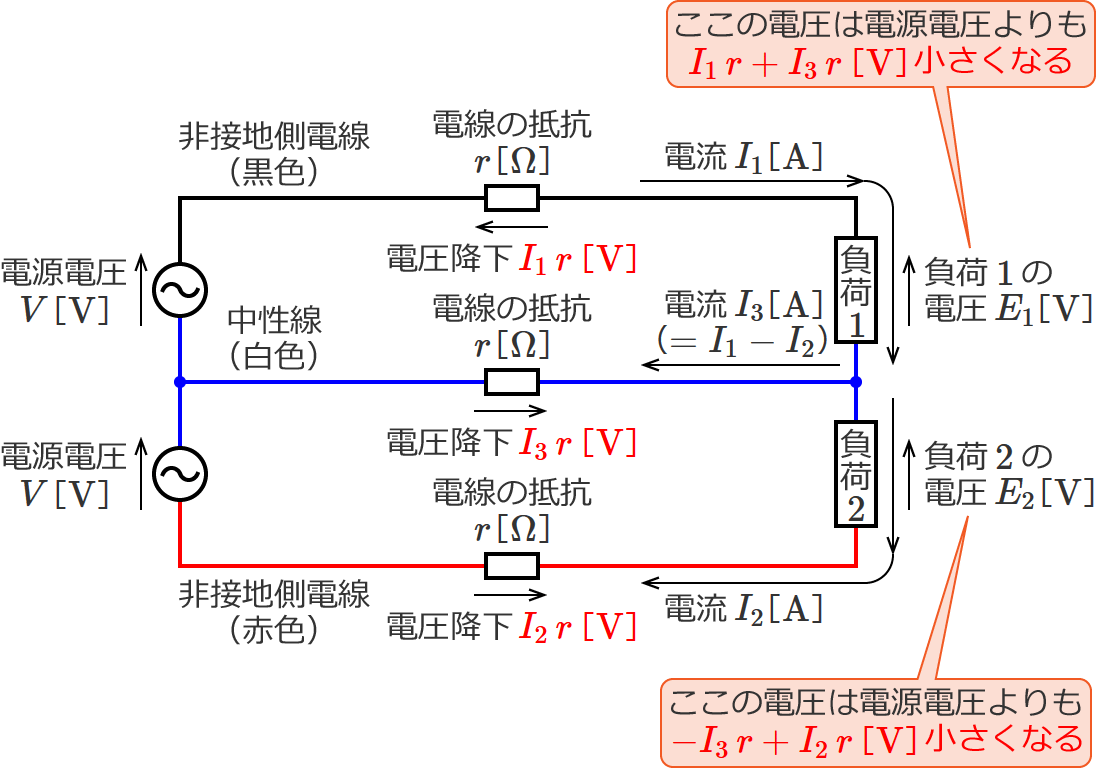
なので、負荷1側（上側）の電圧降下（$V-E_1$［$\mathrm{V}$］）は、
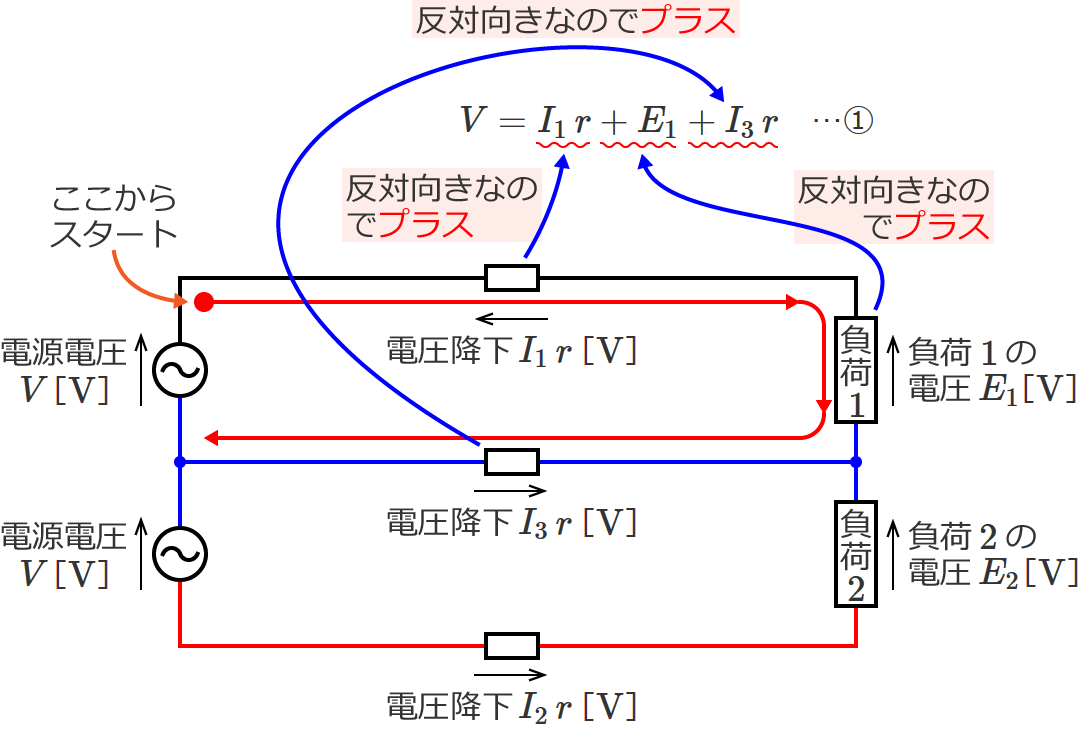
$V=I_1\, r+E_1+I_3\, r$ …① より、
電圧降下 $=V-E_1=I_1\, r+I_3\, r$
$\therefore$ 電圧降下 $=I_1\, r+I_3\, r$ ［$\mathrm{V}$］
になります。
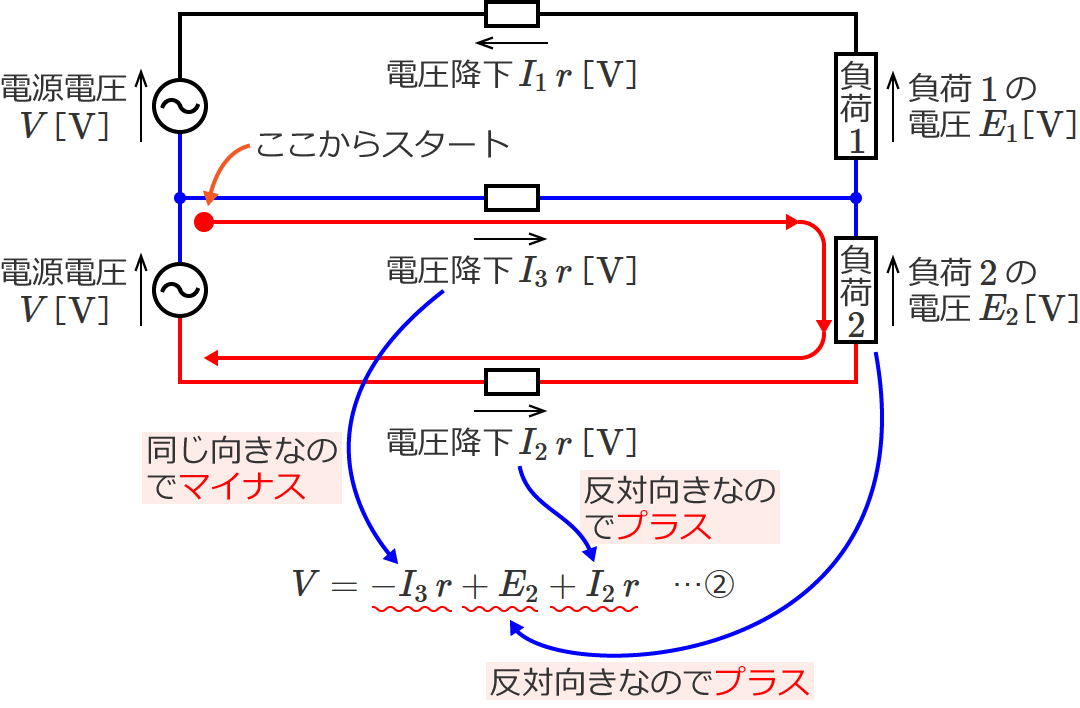
また、負荷2側（下側）の電圧降下（$V-E_2$［$\mathrm{V}$］）は、
$V=-I_3\, r+E_2+I_2\, r$ …② より、
電圧降下 $=V-E_2=-I_3\, r+I_2\, r$
$\therefore$ 電圧降下 $=-I_3\, r+I_2\, r$ ［$\mathrm{V}$］
になります。
中性線に右向きの電流が流れる場合
中性線に右向きの電流が流れる場合というのは、次の図で電流 $I_1$［$\mathrm{A}$］が電流 $I_2$［$\mathrm{A}$］よりも小さい場合です。このとき、$I_2$ から $I_1$ を引いた大きさの電流（図の $I_3$（$=I_2-I_1$））が右向きに流れます。
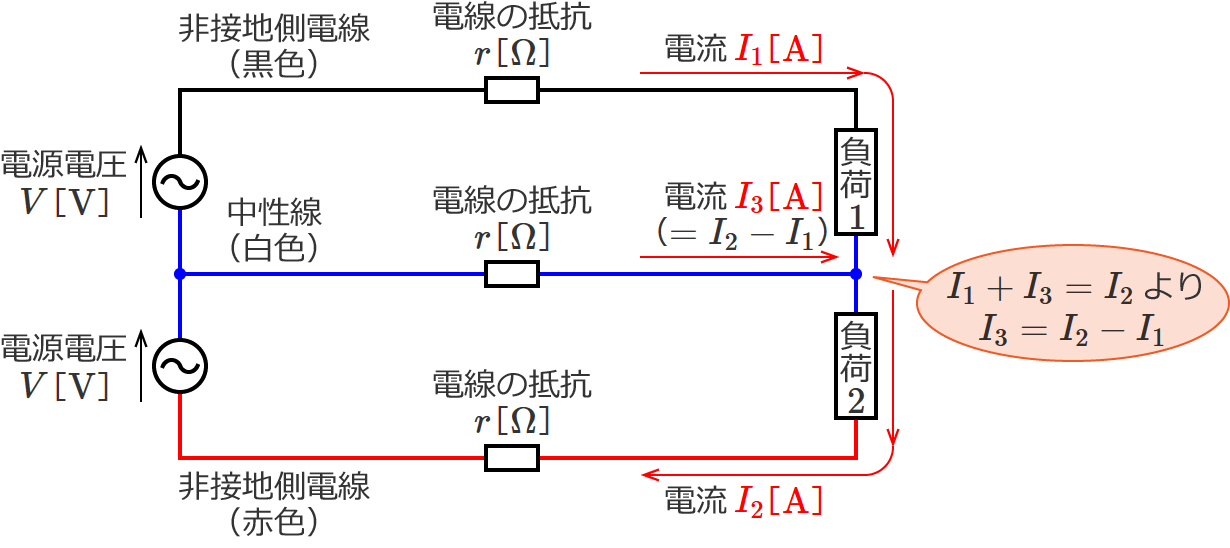
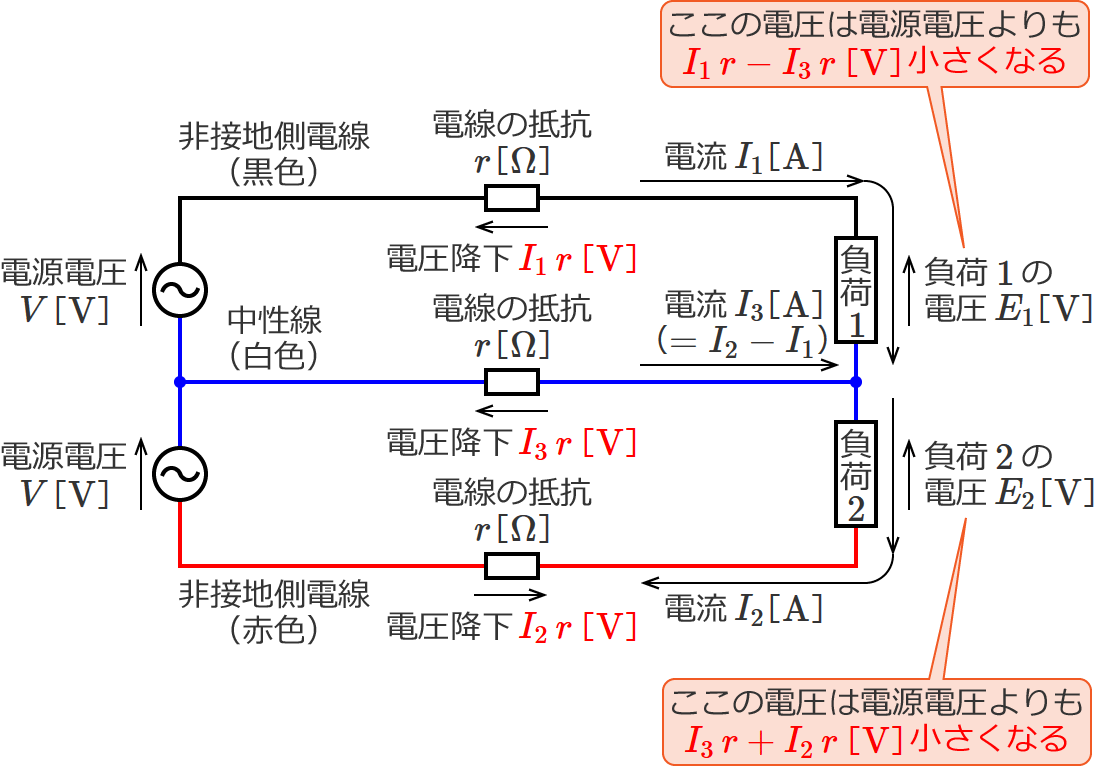
この場合の各電線の抵抗における電圧降下は、次のようになります。
なので、負荷1側（上側）の電圧降下（$V-E_1$［$\mathrm{V}$］）は、
$V=I_1\, r+E_1-I_3\, r$ より、
電圧降下 $=V-E_1=I_1\, r-I_3\, r$
$\therefore$ 電圧降下 $=I_1\, r-I_3\, r$ ［$\mathrm{V}$］
になります。
また、負荷2側（下側）の電圧降下（$V-E_2$［$\mathrm{V}$］）は、
$V=I_3\, r+E_2+I_2\, r$ より、
電圧降下 $=V-E_2=I_3\, r+I_2\, r$
$\therefore$ 電圧降下 $=I_3\, r+I_2\, r$ ［$\mathrm{V}$］
になります。
電圧降下と負荷電圧の矢印の向きの決め方
電圧降下と負荷電圧の矢印の向きは、電流の向きと反対に書けばいいです。
①、②式のプラス、マイナスの決め方
①、②式のプラス、マイナスはそれぞれの電源からたどって、たどった方向と電圧降下（または負荷電圧）の矢印の向きが反対だったらプラス、同じだったらマイナスにすればいいです。（電源電圧 $V=\cdots$ の式で書く場合）
三相3線式配電線の電圧降下
三相3線式配電線の回路は、次のようになります。（負荷側がY結線（スター結線）で、負荷は抵抗負荷とします。）
この三相3線式回路の電線1本の抵抗を $r$［$\Omega$］とし、電流 $I$［$\mathrm{A}$］の流れも書くと次のようになります。
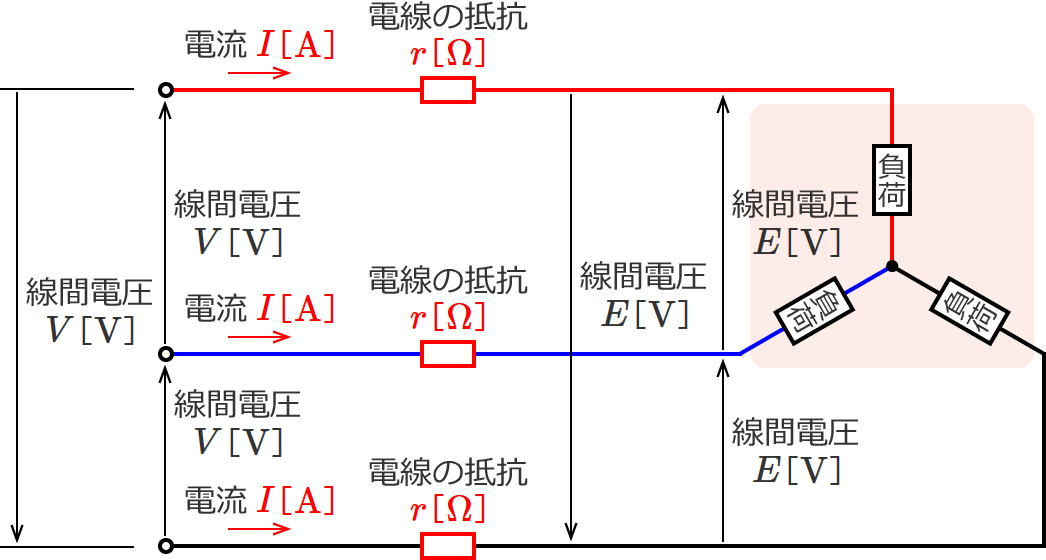
この場合、電圧降下（$V-E$［$\mathrm{V}$］）はいくらでしょうか？
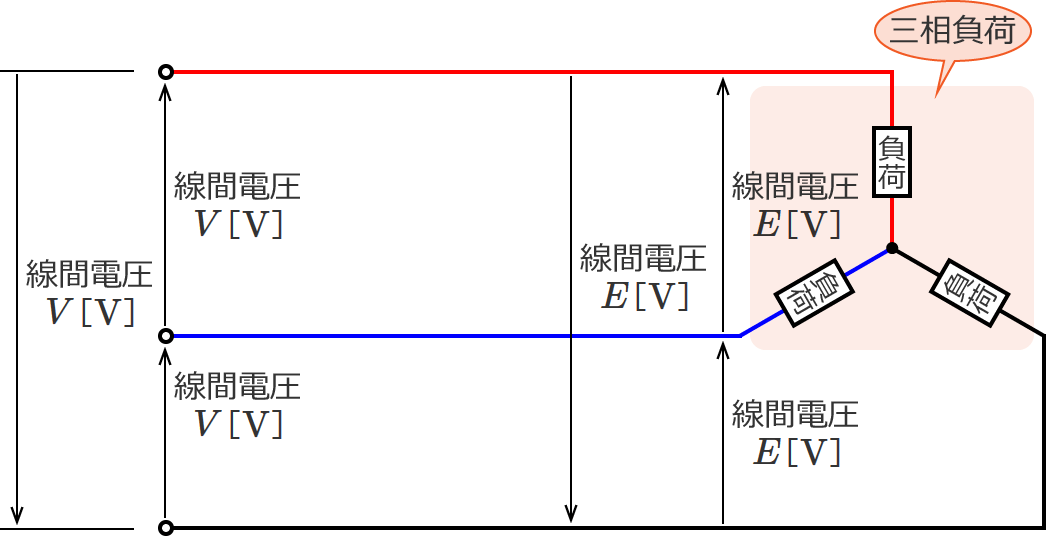
電圧降下（$V-E$［$\mathrm{V}$］）を求めるために、回路の電圧を線間電圧から相電圧に直して考えます。電源側の電圧と負荷側の電圧を相電圧で表わすと次のようになります。
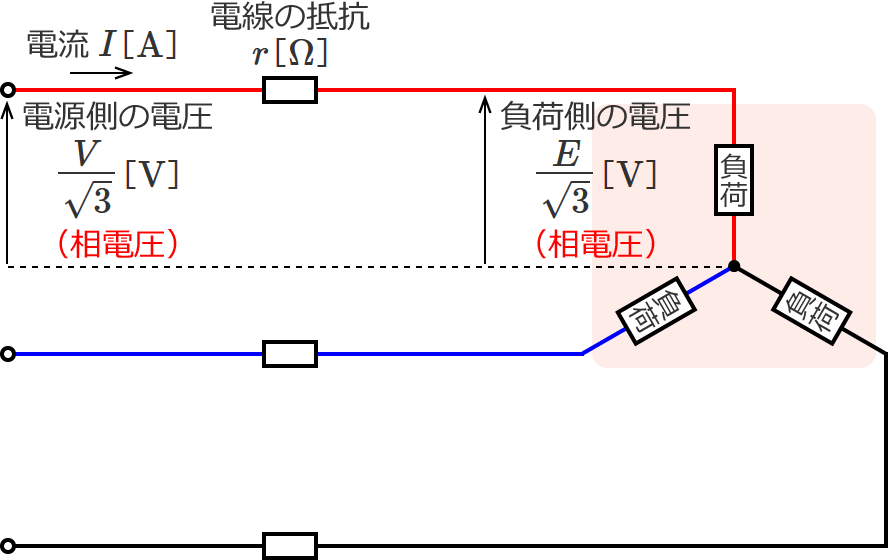
すると、電圧と電流の関係は次のようになります。
$\dfrac{V}{\sqrt{3}} =Ir+\dfrac{E}{\sqrt{3}}$ 、 $\dfrac{V}{\sqrt{3}} -\dfrac{E}{\sqrt{3}} =Ir$ 、 $V-E=\sqrt{3} Ir$
なので、三相3線式回路の電圧降下（$V-E$）は、
$\therefore V-E=\sqrt{3} Ir$ ［$\mathrm{V}$］
になります。
$\sqrt{3} Ir$［$\mathrm{V}$］は、電源の線間電圧と負荷にかかる線間電圧の差であることに注意しましょう。
配電線の電圧降下のまとめ
配電線の電圧降下の式をまとめると次の表のようになります。
| 配電方式 | 電圧降下の式 |
|---|---|
| 単相2線式 | $2Ir$ |
| 単相3線式 | $Ir$ （中性線の電流がゼロの場合） |
| 上側のループ：$I_1\, r+I_3\, r$ 下側のループ：$-I_3\, r+I_2\, r$ （中性線の電流が左向きの場合） |
|
| 上側のループ：$I_1\, r-I_3\, r$ 下側のループ：$I_3\, r+I_2\, r$ （中性線の電流が右向きの場合） |
|
| 三相3線式 | $\sqrt{3} Ir$ |
赤文字の式は、第二種電気工事士の学科試験の問題を解くときにもよく使われるので、公式としておぼえておくといいでしょう。
スポンサーリンク
スポンサーリンク
三相3線式配電線の線間電圧と相電圧の関係については、こちらの配電線（配電方式）の種類のページを参考にしてみましょう。
それから、三相3線式の電圧降下の式の係数「$\sqrt{3}$」と電力損失の式の係数「$3$」をゴチャゴチャにおぼえてしまっている人がいますので気を付けましょう。（配電線の電力損失については、こちらの配電線の電力損失のページを参考にしてみてください。）
スポンサーリンク
配電線の電圧降下 関連ページ
- 配電線とは？
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない「配電線とは？」についてまとめています。
- 配電線（配電方式）の種類
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない単相2線式、単相3線式、三相3線式などの「配電線（配電方式）の種類」についてまとめています。
- 配電方式と消費電力
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、三相3線式などの配電方式ごとの負荷の消費電力についてまとめています。
- 配電線の電力損失
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式などの配電線の電力損失についてまとめています。
- 配電線の断線
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式（Y結線）、三相3線式（Δ結線）などの配電線が「断線するとどうなるか？」についてまとめています。
