スポンサーリンク
配電線の電力損失
※ページ内にPR・広告が含まれる場合があります。
配電線では、電力損失が生じます。
電力損失とは、電源から送られた電力が負荷とは別のところでムダに失われてしまうことをいいます。(電力を損失するってことです。)
では何故、配電線では電力損失が生じてしまうのでしょうか?
電線は電力をムダに使わないように、できるだけ抵抗が小さい材料を使って作られています。ですが、配電線って長ーいですよね?(短いのもないわけではないですが…)
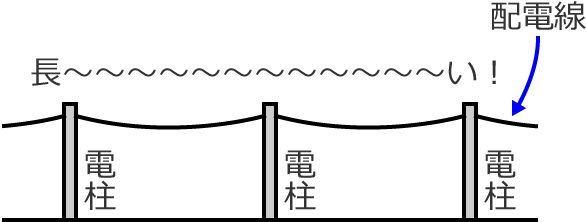
電線の抵抗のページで解説したように、電線の長さが2倍、3倍…と長くなると、抵抗も2倍、3倍…と大きくなります。
つまり、抵抗が小さい材料を使った電線でも、電線の長さが長くなるとその抵抗が無視できないくらいになってしまうのです。回路図で書いてみると次のようになります。
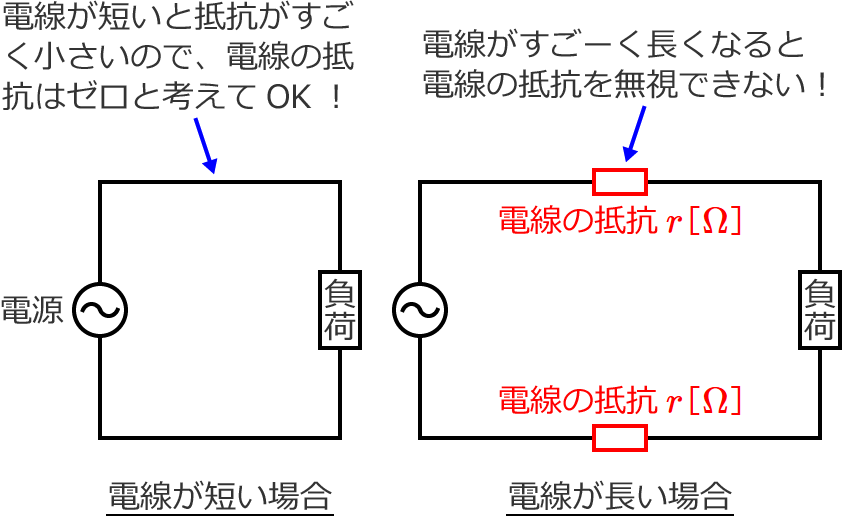
左の図は電線が短く、電線の抵抗は無視できるくらい小さいため、回路図に電線の抵抗は書かれていません。(電線の抵抗=ゼロ(ゼロオーム)と考えているということ。)
右の図は電線の長さがすごく長く、電線の抵抗を無視できないため、回路図に電線の抵抗を書いています。
左の図はここではどうでもいいので、右の図について考えてみましょう。
右の図は電源につながっているので、回路に電流が流れます。
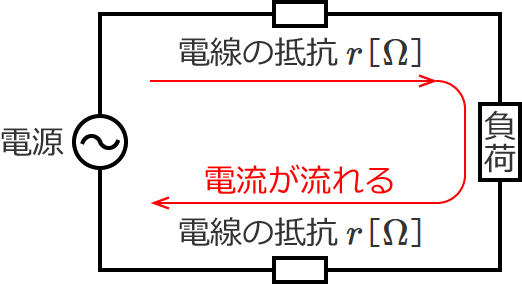
この図をよく見ると(よく見なくても)、電線の抵抗に電流が流れていますよね?
抵抗に電流が流れるとどうなるんでしたっけ?
「オームの法則により電圧(電圧降下)が生じます!」って、それはそれで正しいのですが、抵抗に電流が流れると、
「電流2×抵抗」の大きさの電力を消費します!
これが電線の電力損失で、電線が配電線であれば配電線の電力損失ということになります。
つまり、配電線は長いので電線の抵抗により電力損失が生じてしまうってことです。
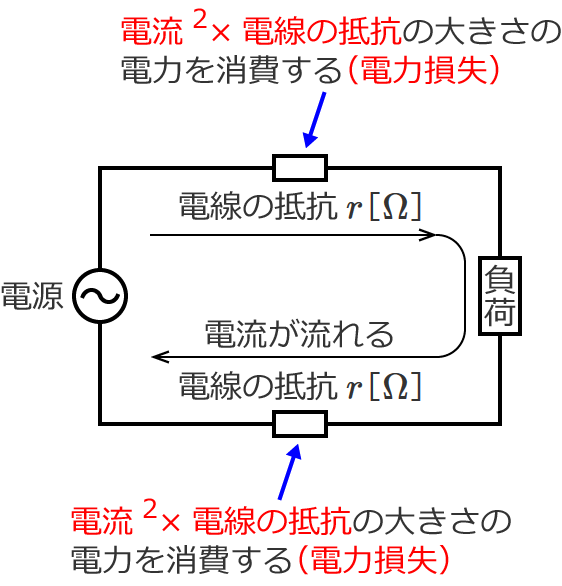
「電流2×電線の抵抗」は、電線1本分の電力損失の大きさになります。なので、電線2本分の電力損失を求めるときには、「2×電流2×電線の抵抗」となることに注意しましょう。(2本分だから2倍する。)
あとそれから、電力損失の単位は電力と同じ「$\mathrm{W}$(ワット)」になります。
スポンサーリンク
単相2線式配電線の電力損失
単相2線式配電線の電線1本あたりの抵抗を $r$[$\Omega$]、回路に流れる電流を $I$[$\mathrm{A}$]とすると、回路図は次のようになります。(負荷は抵抗負荷とします。)
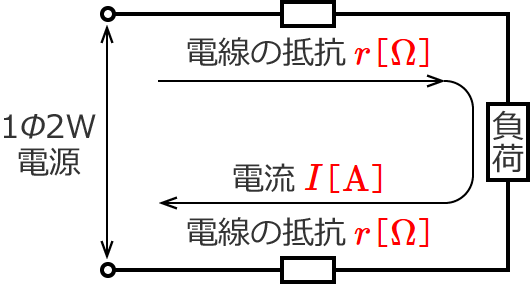
図中の $1\phi 2\mathrm{W}$ は、単相2線式という意味です。
電線1本あたりの抵抗は $r$[$\Omega$]で、その抵抗には $I$[$\mathrm{A}$]の電流が流れているので、電線1本あたりの電力損失 $P_{L1}$[$\mathrm{W}$]は、
$P_{L1}=I^2\, r$ [$\mathrm{W}$] になります。
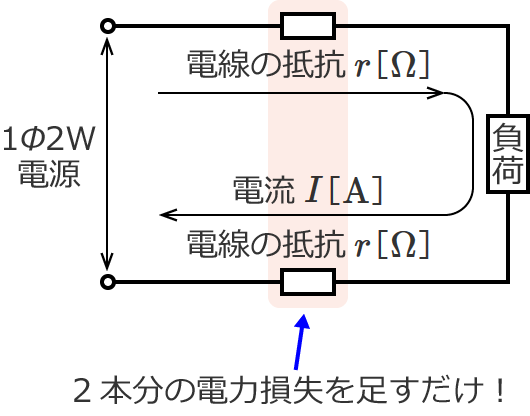
なので、電線2本分の電力損失 $P_L$[$\mathrm{W}$]は、$P_{L1}$ を2倍(2本分という意味)して、
$P_L=2\times P_{L1}=2\times I^2\, r=2I^2\, r$
$\therefore P_L=2I^2\, r$ [$\mathrm{W}$]
になります。
単相3線式配電線の電力損失(中性線の電流がゼロの場合)
単相3線式配電線の電線1本あたりの抵抗を $r$[$\Omega$]、回路に流れる電流を $I$[$\mathrm{A}$]とすると、回路図は次のようになります。(中性線の電流がゼロで、負荷は抵抗負荷とします。)
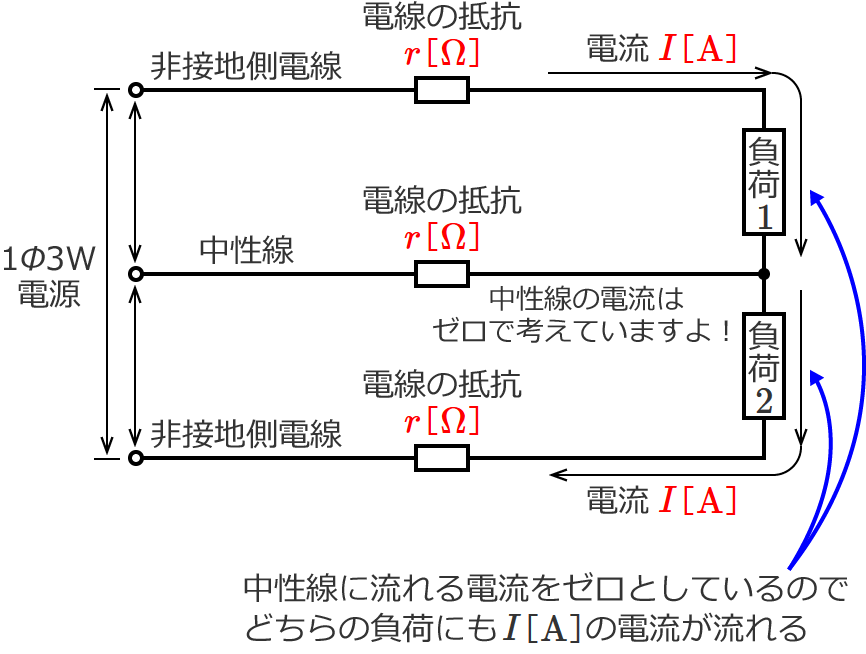
図中の $1\phi 3\mathrm{W}$ は、単相3線式という意味です。
上側の電線1本の電力損失
図の上側の電線の抵抗は $r$[$\Omega$]で、その抵抗には $I$[$\mathrm{A}$]の電流が流れているので、ここの電線の電力損失 $P_{L1}$[$\mathrm{W}$]は、
$\therefore P_{L1}=I^2\, r$ [$\mathrm{W}$] …① になります。
真中の電線1本の電力損失
図の真中の電線の抵抗は $r$[$\Omega$]で、その抵抗に流れる電流はゼロなので、ここの電線の電力損失 $P_{L2}$[$\mathrm{W}$]は、
$P_{L2}=0^2\times r=0$
$\therefore P_{L2}=0$ [$\mathrm{W}$] …② になります。(電流がゼロのときは電力損失もゼロになります。)
下側の電線1本の電力損失
図の下側の電線の抵抗は $r$[$\Omega$]で、その抵抗には $I$[$\mathrm{A}$]の電流が流れているので、ここの電線の電力損失$P_{L3}$[$\mathrm{W}$]は、
$\therefore P_{L3}=I^2\, r$ [$\mathrm{W}$] …③ になります。
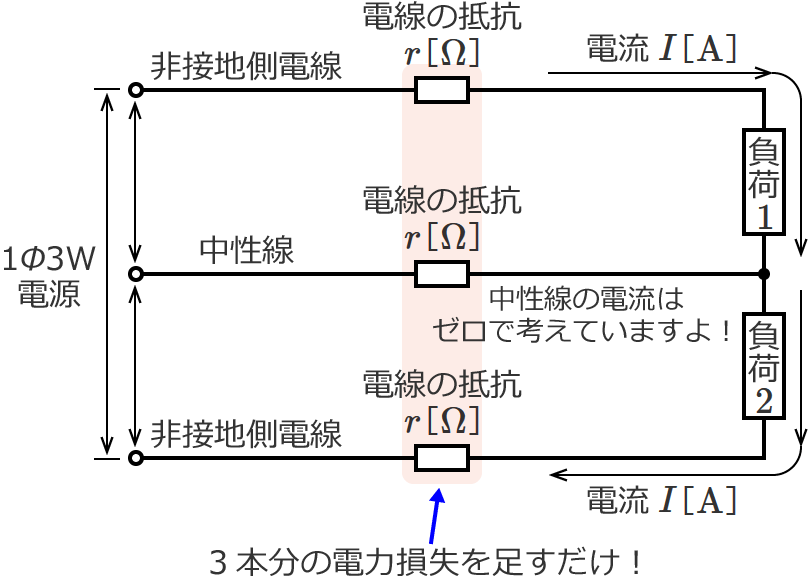
以上より、電線3本分の電力損失 $P_L$[$\mathrm{W}$]は、①、②、③を足して、
$P_L=P_{L1}+P_{L2}+P_{L3}$ $=I^2\, r+0+I^2\, r$ $=2I^2\, r$
$\therefore P_L=2I^2\, r$ [$\mathrm{W}$]
になります。
スポンサーリンク
スポンサーリンク
三相3線式配電線の電力損失
三相3線式配電線の電線1本あたりの抵抗を $r$[$\Omega$]、回路に流れる電流を図のように $I$[$\mathrm{A}$]とすると、回路図は次のようになります。(負荷は抵抗負荷とします。)
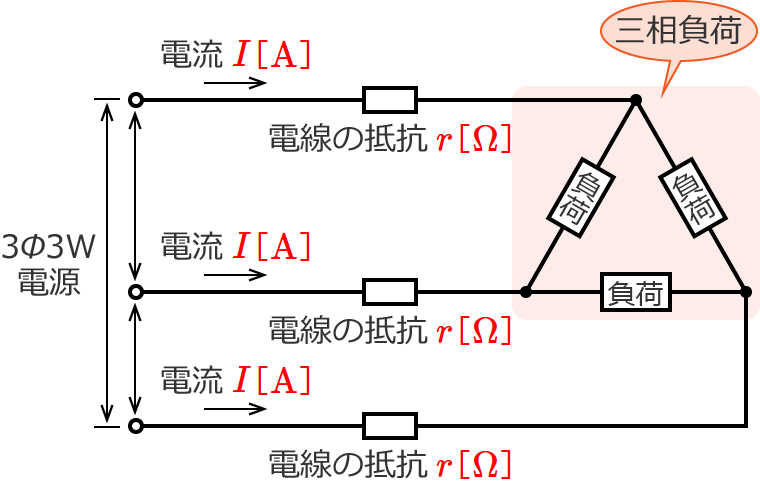
図中の $3\phi 3\mathrm{W}$ は、三相3線式という意味です。
電線1本あたりの抵抗は $r$[$\Omega$]で、その抵抗には $I$[$\mathrm{A}$]の電流が流れているので、電線1本あたりの電力損失 $P_{L1}$[$\mathrm{W}$]は、
$P_{L1}=I^2\, r$ [$\mathrm{W}$] になります。
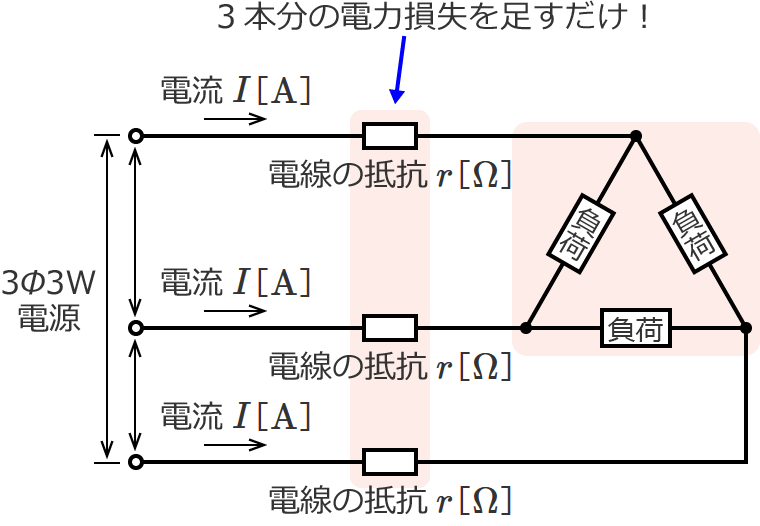
なので、電線3本分の電力損失 $P_L$[$\mathrm{W}$]は、$P_{L1}$ を3倍(3本分という意味)して、
$P_L=3\times P_{L1}=3\times I^2\, r=3I^2\, r$
$\therefore P_L=3I^2\, r$ [$\mathrm{W}$]
になります。
配電線の電力損失のまとめ
配電線の電力損失の式をまとめると、次の表のようになります。
| 配電方式 | 電力損失の式 |
|---|---|
| 単相2線式 | $P_L=2I^2\, r$ |
| 単相3線式 | $P_L=2I^2\, r$ |
| 三相3線式 | $P_L=3I^2\, r$ |
表中の単相3線式の電力損失 $P_L$ の式は、中性線の電流がゼロの場合です。
この3つの式は、第二種電気工事士の学科試験の問題を解くときにも度々使われるので、公式としておぼえておくようにしましょう。
スポンサーリンク
スポンサーリンク
三相3線式の電力損失の式の係数「$3$」と電圧降下の式の係数「$\sqrt{3}$」をゴチャゴチャにおぼえてしまっている人がいますので気を付けましょう。(配電線の電圧降下については、こちらの配電線の電圧降下のページを参考にしてみてください。)
スポンサーリンク
配電線の電力損失 関連ページ
- 配電線とは?
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない「配電線とは?」についてまとめています。
- 配電線(配電方式)の種類
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない単相2線式、単相3線式、三相3線式などの「配電線(配電方式)の種類」についてまとめています。
- 配電方式と消費電力
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、三相3線式などの配電方式ごとの負荷の消費電力についてまとめています。
- 配電線の電圧降下
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式などの配電線の電圧降下についてまとめています。
- 配電線の断線
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式(Y結線)、三相3線式(Δ結線)などの配電線が「断線するとどうなるか?」についてまとめています。


