スポンサーリンク
配電方式と消費電力
※ページ内にPR･広告が含まれる場合があります。
消費電力とは、
電源に接続された負荷が消費する電力
のことをいいます。（ま、そのまんまなんですが…）
例えば次のように、電圧 $V$［$\mathrm{V}$］ の交流電源に抵抗負荷（抵抗の負荷）が接続されている簡単な回路を考えてみます。
この回路に流れる電流を $I$［$\mathrm{A}$］とすると、抵抗負荷には $V$［$\mathrm{V}$］の電圧がかかって、$I$［$\mathrm{A}$］の電流が流れることになります。
すると、この場合の負荷の消費電力 $P$［$\mathrm{W}$］は、
$\therefore P=VI$ ［$\mathrm{W}$］
になります。
電力を求める式は「電力＝電圧×電流」でしたので、この場合は、単に抵抗の電力を計算すると、それが消費電力なんです。ということです。
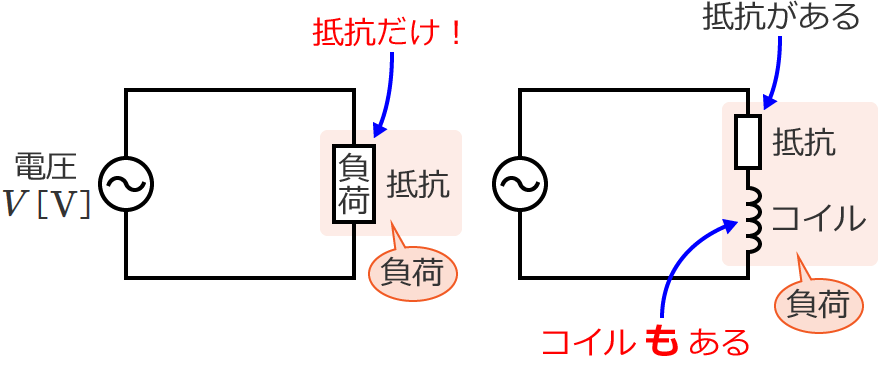
負荷が抵抗だけの場合は、このように電圧と電流をかけ算するだけでいいのですが、負荷にコイルやコンデンサなどがあると、
単純に「電圧×電流」で求めることができません。
では、どうやって求めればいいのでしょうか？
スポンサーリンク
単相2線式配電線の負荷の消費電力
次のように、負荷として抵抗とコイルが直列接続された単相2線式配電線の回路を考えてみましょう。
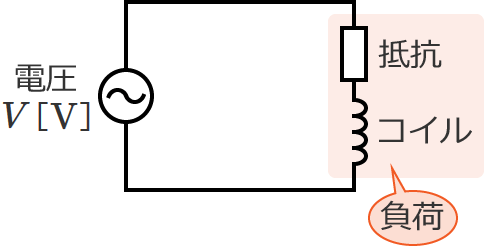
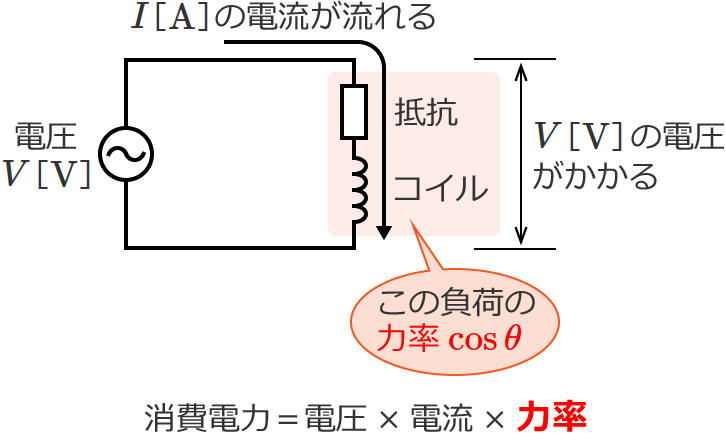
電源電圧は $V$［$\mathrm{V}$］なので、この回路に流れる電流を $I$［$\mathrm{A}$］とすると、負荷には $V$［$\mathrm{V}$］の電圧がかかって $I$［$\mathrm{A}$］の電流が流れることになります。
この回路の消費電力を求めるときに、先ほどの抵抗だけの回路のように、
「電圧×電流＝V×I［W］」とすると間違いです！
何故でしょうか？
2つの回路を見比べてみると、コイルがあるか？ないか？が違いますよね。
コイルがあると何を考えなければならないでしょうか？
なんとなく分かると思いますが、交流回路の計算をするときにコイルやコンデンサがある場合には力率を考えなければなりません。
で、負荷の力率を $\cos\theta$ とすると、単相2線式配電線の負荷の消費電力 $P$［$\mathrm{W}$］は、
$\therefore P=VI\cos\theta$ ［$\mathrm{W}$］
と表わされ、電圧と電流をかけたものに、さらに力率をかけた形の式になります。
このように、コイルやコンデンサがあるときには力率を考慮しなくてはならないので注意しましょう！
ちなみに、抵抗だけの回路の場合には負荷の力率は $\cos\theta =1$ になるので、これを消費電力の式に代入してみると、
$P=VI\cos\theta =VI\times 1=VI$
$\therefore P=VI$ ［$\mathrm{W}$］
となり、電圧と電流をかけただけの式になります。
スポンサーリンク
スポンサーリンク
三相3線式配電線の負荷の消費電力
次は、三相3線式配電線の負荷の消費電力について考えてみましょう。
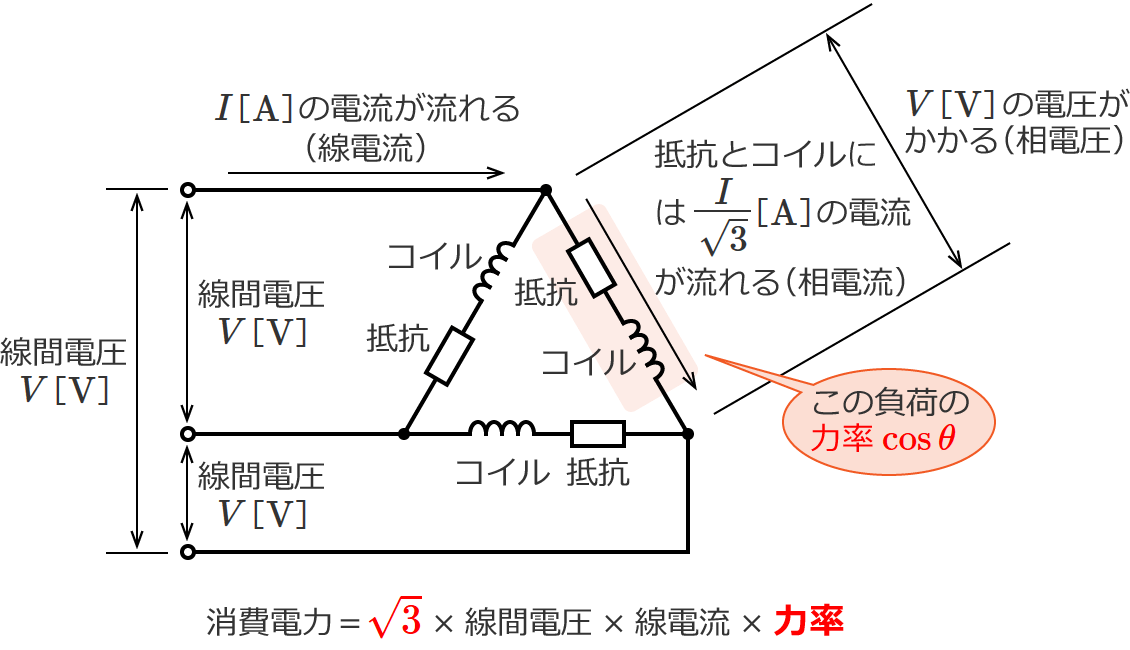
次のように、一相の負荷として抵抗とコイルが直列接続された三相3線式配電線（負荷Δ結線（デルタ結線））の回路を考えてみます。
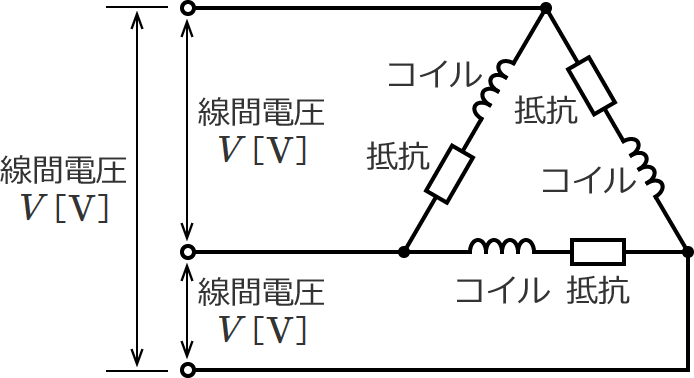
電源電圧（線間電圧）は $V$［$\mathrm{V}$］なので、この回路に流れる電流（線電流）を $I$［$\mathrm{A}$］とすると、負荷（抵抗とコイルの直列接続）には $V$［$\mathrm{V}$］の電圧がかかって $\dfrac{I}{\sqrt{3}}$［$\mathrm{A}$］ の電流が流れることになります。（Δ結線（デルタ結線）の線電流と相電流の関係式より、相電流 $=\dfrac{\text{線電流}}{\sqrt{3}}$ ですよ。）
この回路は三相なので負荷が3つ（三相分）ありますが、一相だけ取り出して考えてみましょう。一相だけ取り出すと、次のような回路になります。（電流は相電流ですよ！）
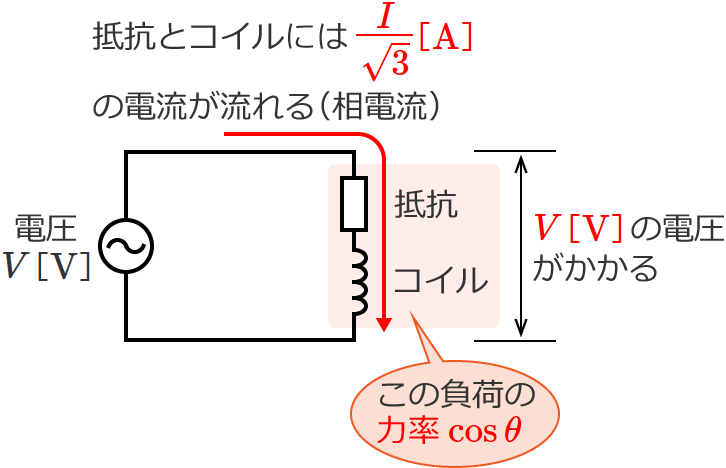
これを先ほどの単相2線式と同じように考えて、負荷（抵抗とコイルの直列接続）の力率を $\cos\theta$ としてこの回路の消費電力 $P_1$［$\mathrm{W}$］を求めてみると、
$P_1=V\times\dfrac{I}{\sqrt{3}}\cos\theta =\dfrac{VI}{\sqrt{3}}\cos\theta$
$\therefore P_1=\dfrac{VI}{\sqrt{3}}\cos\theta$ ［$\mathrm{W}$］
となり、これが一相分の消費電力になります。
三相分の消費電力は負荷3つ分なので、一相分の消費電力 $P_1$［$\mathrm{W}$］を3倍すれば三相分の消費電力が求められます。一相分の消費電力 $P_1$［$\mathrm{W}$］を3倍すると、
$3\times P_1=3\times\dfrac{VI}{\sqrt{3}}\cos\theta$ $=\dfrac{3\times\sqrt{3}\times VI}{\sqrt{3}\times\sqrt{3}}\cos\theta$ $=\dfrac{3\sqrt{3}}{3} VI\cos\theta$ $=\sqrt{3} VI\cos\theta$
したがって、三相3線式配電線の負荷の消費電力 $P$［$\mathrm{W}$］は、
$P=\sqrt{3} VI\cos\theta$ ［$\mathrm{W}$］
になります。
配電方式と負荷の消費電力のまとめ
配電方式と負荷の消費電力の式をまとめると、次の表のようになります。
| 配電方式 | 消費電力の式 |
|---|---|
| 単相2線式 | $P=VI$ （負荷が抵抗だけの場合（力率 $\cos\theta =1$）） |
| $P=VI\cos\theta$ （負荷にコイルやコンデンサがある場合（力率 $\cos\theta\neq 1$）） |
|
| 三相3線式 | $P=\sqrt{3} VI\cos\theta$ |
赤文字の式は第二種電気工事士学科試験の計算問題を解くときによく使うので、公式としておぼえておくといいでしょう。
スポンサーリンク
スポンサーリンク
単相交流回路の3つの電力（有効電力、無効電力、皮相電力）については有効電力・無効電力・皮相電力（交流回路の3つの電力）のページで、三相3線式の電力の式については三相電力の公式はなぜ√3倍なのか？のページでも解説していますので、参考にしてみるといいと思います。
三相3線式の線電流と相電流の関係については、こちらの配電線（配電方式）の種類のページを参考にしてみましょう。
配電線（配電方式）の種類 ←BACK
NEXT→ 配電線の電圧降下
スポンサーリンク
配電方式と消費電力 関連ページ
- 配電線とは？
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない「配電線とは？」についてまとめています。
- 配電線（配電方式）の種類
- 第二種電気工事士学科試験の「配電理論」分野でおぼえておかなければならない単相2線式、単相3線式、三相3線式などの「配電線（配電方式）の種類」についてまとめています。
- 配電線の電圧降下
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式などの配電線の電圧降下についてまとめています。
- 配電線の電力損失
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式などの配電線の電力損失についてまとめています。
- 配電線の断線
- 第二種電気工事士学科試験の「配電理論」分野で出題される単相2線式、単相3線式、三相3線式（Y結線）、三相3線式（Δ結線）などの配電線が「断線するとどうなるか？」についてまとめています。
