スポンサーリンク
RL直列回路の過渡現象の解き方
※ページ内にPR・広告が含まれる場合があります。
RL直列回路に流れる電流の求め方
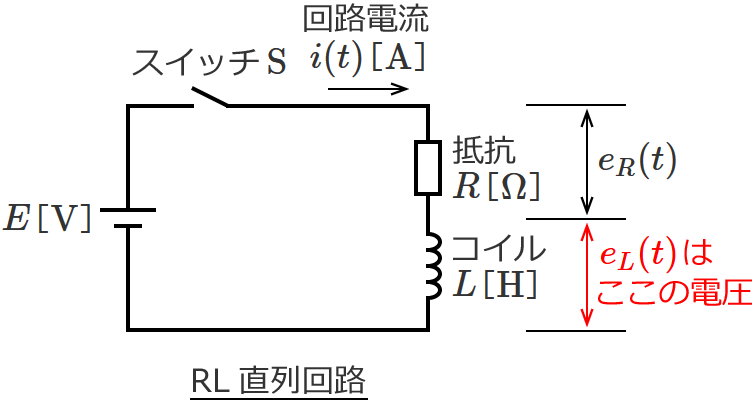
次の図のように、抵抗 $R$[$\Omega$]、コイル $L$[$\mathrm{H}$]、直流電源 $E$[$\mathrm{V}$]、スイッチ $\mathrm{S}$ からなるRL直列回路があるとします。
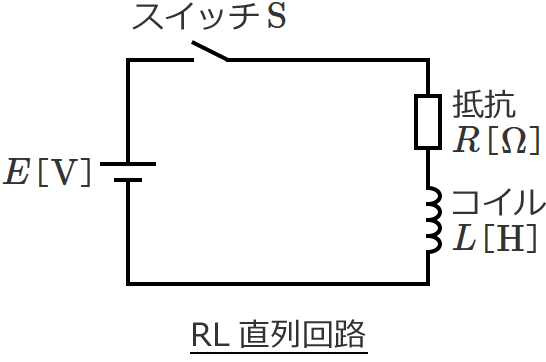
この回路のスイッチをONすると過渡現象が起こるため、スイッチをONすると回路に流れる電流は時間的に変化し、その後ある程度の時間が経過すると一定値に落ち着きます。
このような時間的に変化する過渡現象の電圧や電流を求めるときは、次のような手順で解いていきます。
回路の過渡現象を解く基本的な手順
❶対象の回路の回路方程式(微分や積分が含まれる)をたてる
❷初期条件を考慮して❶の微分方程式(または積分方程式)を解く
ざっくりいえばこれだけですが、上に記載した解く手順❷の「微分方程式(または積分方程式)を解く」ことが回路によっては大変になったりします。
それでは、RL直列回路に流れる電流を求めてみます。
スポンサーリンク
まず初めに、回路の回路方程式をたてます。
回路に流れる電流を $i(t)$[$\mathrm{A}$]として、
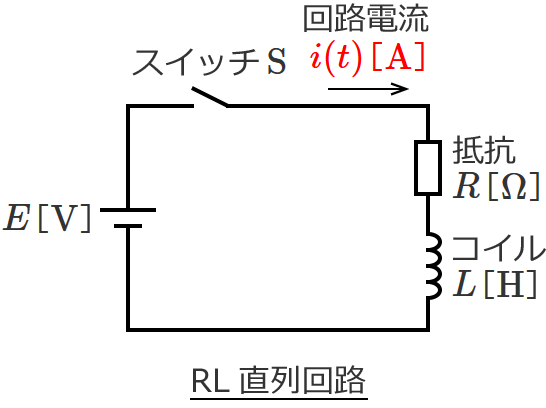
この回路にキルヒホッフの第二法則(電圧則)を適用すれば、回路方程式は次の①式(微分方程式)で与えられます。
$E = R \, i(t) + L \dfrac{d \, i(t)}{dt}$ …①
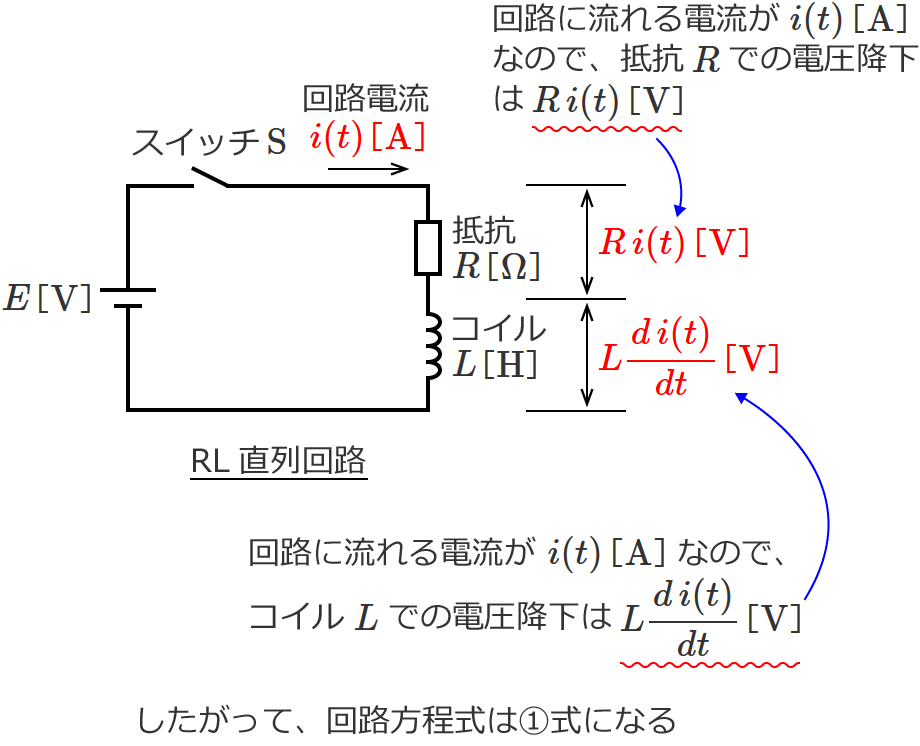
回路方程式がたてられたので、あとは①式の微分方程式を解くだけです。
微分方程式は、その方程式の形で色々な解き方があったり、ラプラス変換を使って解いたりすることができますが、ここでは微分方程式の解法の一つである変数分離法を使って解くことにします。
変数分離法は名前の通り、変数を左辺と右辺に分離して解いていく方法です。
①式の場合、電流 $i(t)$ と時間 $t$ が変数なので、電流 $i(t)$ に関するものは左辺に、時間 $t$ に関するものは右辺になるように①式を変形します。(電源電圧 $E$ と抵抗 $R$ とコイルのインダクタンス $L$ は定数なので、左辺と右辺どちらにあってもいいです。)
①式の $L \dfrac{d \, i(t)}{dt}$ を左辺に、$E$ を右辺に移動します。すると、
$L \dfrac{d \, i(t)}{dt} = E - R \, i(t)$
上式の両辺を $L$ で割ります。
$\dfrac{d \, i(t)}{dt} = \dfrac{E - R \, i(t)}{L}$
両辺を $E - R \, i(t)$ で割ります。
$\dfrac{1}{E - R \, i(t)} \cdot \dfrac{d \, i(t)}{dt} = \dfrac{1}{L}$
両辺に $dt$ をかけます。
$\dfrac{1}{E - R \, i(t)} \cdot d \, i(t) = \dfrac{1}{L} \cdot dt$
計算をしやすくするため、もうちょっと変形しておきます。両辺にマイナスをかけて、
$\dfrac{1}{R \, i(t) - E} \cdot d \, i(t) = -\dfrac{1}{L} \cdot dt$
両辺の分母を $R$ で割って、
$\dfrac{1}{\dfrac{R \, i(t) - E}{R}} \cdot d \, i(t) = -\dfrac{1}{\dfrac{L}{R}} \cdot dt$
$\therefore \dfrac{1}{i(t) - \dfrac{E}{R}} \cdot d \, i(t) = -\dfrac{R}{L} \cdot dt$ …②
これで左辺は電流 $i(t)$(変数)に関するもの、右辺は時間 $t$(変数)に関するものとなり、2つの変数を左辺と右辺に分離することができました。(定数は変数ではないので、左辺にあっても右辺にあってもいいです。)
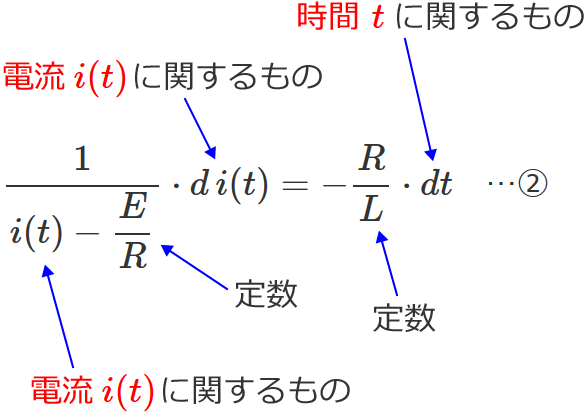
変数を分離できたので、あとは両辺を積分して計算を続けていきます。
②式の両辺を積分すると(両辺に積分記号を付けるだけ)、
$\displaystyle\int \dfrac{1}{i(t) - \dfrac{E}{R}} \, d \, i(t) = -\int \dfrac{R}{L} \, dt$ …③
となります。では、③式の左辺から計算してみましょう。
③式の左辺は $\displaystyle\int \dfrac{1}{x} \, dx$ の形の積分なので、積分の公式より、
③式の左辺 $= \displaystyle\int \dfrac{1}{i(t) - \dfrac{E}{R}} \, d \, i(t)$
$= \log_e \left| i(t) - \dfrac{E}{R} \right| + A$ ( $A$ は積分定数) …④
④式に絶対値が付いているので、これを外しましょう。
絶対値の中は $i(t) - \dfrac{E}{R}$ ですが、$i(t)$ は回路に流れる電流で、$\dfrac{E}{R}$ はコイル $L$ が短絡された状態(つまり、定常状態)での電流なので、$i(t) \leqq \dfrac{E}{R}$ となり、絶対値の中は常にゼロ以下になります。
なので、絶対値の中 $\left( i(t) - \dfrac{E}{R} \right)$ にマイナスをかけると絶対値を外すことができます。つまり、
$\log_e \left| i(t) - \dfrac{E}{R} \right| + A$ $= \log_e \left( \dfrac{E}{R} - i(t) \right) + A$ …⑤
となります。したがって④式と⑤式より、
③式の左辺 $= \log_e \left( \dfrac{E}{R} - i(t) \right) + A$ …⑥
となります。これで③式の左辺は計算できたので、次は③式の右辺について考えます。
$\dfrac{R}{L}$ は定数なので、そのまま積分の外に出します。すると、
③式の右辺 $= -\displaystyle\int \dfrac{R}{L} \, dt$
$= -\dfrac{R}{L} \displaystyle\int \, dt$
$= -\dfrac{R}{L} \cdot t + B$ ( $B$ は積分定数) …⑦
となります。
以上で③式の左辺と右辺が計算できたので、⑥、⑦式を③式に戻すと次の⑧式になります。
$\log_e \left( \dfrac{E}{R} - i(t) \right) + A$ $= -\dfrac{R}{L} \cdot t + B$ …⑧
⑧式には $A$ と $B$ の2つの積分定数があるので、積分定数を $D$ として1つにまとめてしまいます。(つまり、$B - A = D$ とおく)
$\log_e \left( \dfrac{E}{R} - i(t) \right) = -\dfrac{R}{L} \cdot t + D$
対数の定義より、この式を展開すると、
$\dfrac{E}{R} - i(t) = e^{-\frac{R}{L} t + D}$
$\dfrac{E}{R} - i(t) = e^{-\frac{R}{L} t} \cdot e^D$
$\therefore \dfrac{E}{R} - i(t) = e^D \cdot e^{-\frac{R}{L} t}$ …⑨
あとは、⑨式の中の積分定数を求めます。積分定数は回路の初期条件を⑨式に代入すれば求められ、この回路の場合、時間 $t = 0$ のときは回路に流れる電流がゼロなので、初期条件は $t = 0$、$i(t) = 0$ になります。
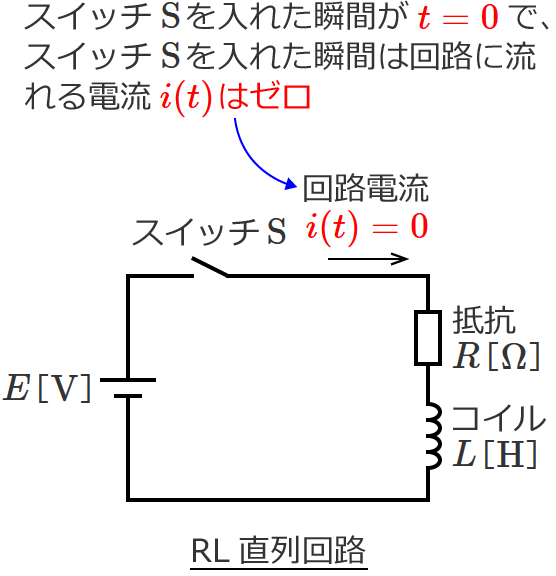
$t = 0$、$i(t) = 0$ を⑨式に代入すると、
$\dfrac{E}{R} - 0 = e^D \cdot e^{-\frac{R}{L} \times 0}$
$\dfrac{E}{R} = e^D \cdot e^0 = e^D \cdot 1 = e^D$
$\therefore e^D = \dfrac{E}{R}$ …⑩
⑩式の両辺の対数をとって $D = \cdots$ を求めてもいいのですが、⑨式をみると $e^D$ をそのまま代入できるので、⑩を⑨式にそのまま代入します。すると、
$\dfrac{E}{R} - i(t) = \dfrac{E}{R} \cdot e^{-\frac{R}{L} t}$
$-i(t) = -\dfrac{E}{R} + \dfrac{E}{R} \cdot e^{-\frac{R}{L} t}$
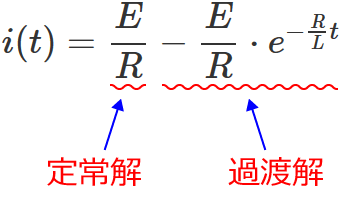
$\therefore i(t) = \dfrac{E}{R} - \dfrac{E}{R} \cdot e^{-\frac{R}{L} t}$ …⑪ (これが回路に流れる電流)
となり、RL直列回路に流れる電流 $i(t)$ が求められました。
ちなみに、この⑪式の右辺の第1項を定常解、第2項を過渡解といいます。
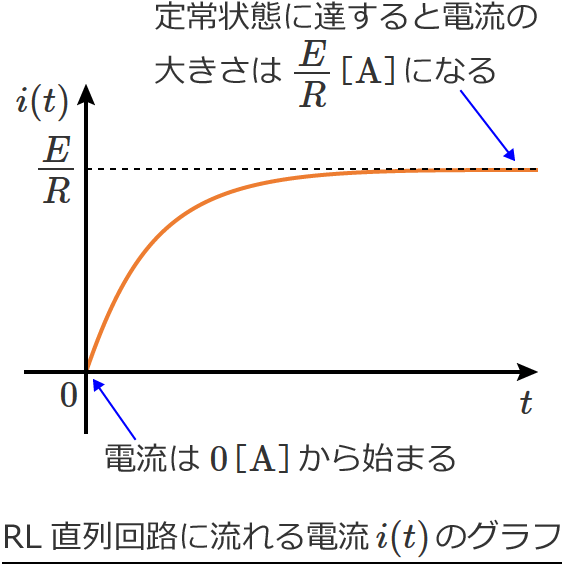
RL直列回路に流れる電流のグラフ
RL直列回路に流れる電流 $i(t)$ が求められたので、次は $i(t)$ のグラフを書いてみます。
さきほど求めた電流の式(⑪式)より、RL直列回路の回路に流れる電流の式は次のようになります。
$i(t) = \dfrac{E}{R} - \dfrac{E}{R} \cdot e^{-\frac{R}{L} t}$ …⑪
⑪式より、回路に流れる電流 $i(t)$ の $t=0$ および $t=\infty$ での値をそれぞれ求めると、
$t=0$ のとき
$i(0)=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L} \times 0}$ (⑪式の $t$ に $0$ を代入した)
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^0$
$=\dfrac{E}{R} -\dfrac{E}{R}\times 1=0$
$\therefore$ $t=0$ のとき $0$
$t=\infty$ のとき
$i(\infty )=\dfrac{E}{R} -\dfrac{E}{R}\cdot e^{-\frac{R}{L} \times\infty}$ (⑪式の $t$ に $\infty$ を代入した)
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot\dfrac{1}{ e^{\frac{R}{L} \times\infty}}$
$=\dfrac{E}{R} -\dfrac{E}{R}\cdot\dfrac{1}{\infty}$
$=\dfrac{E}{R} -0=\dfrac{E}{R}$
$\therefore$ $t=\infty$ のとき $\dfrac{E}{R}$
となります。
また、⑪式の第2項は $e^{-\frac{R}{L} t}$ によって減衰していくので、回路に流れる電流 $i(t)$ のグラフは、時間がたつにつれて増加がゆるやかになる次のようなグラフになります。
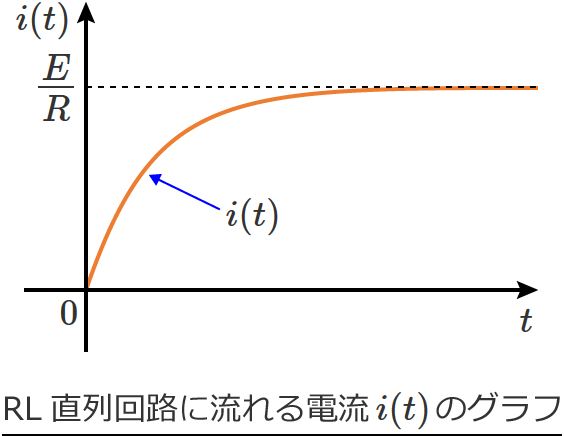
以上でRL直列回路に流れる電流 $i(t)$ のグラフが書けましたが、$i(t)$ のグラフを見るとRL直列回路の場合、回路に流れる電流はゼロから始まり、徐々に大きくなって、ある程度の時間が経過する(定常状態に達するという意味)と $\dfrac{E}{R}$ の大きさの電流が流れ続けることが分かります。
つまり、定常状態に達するとコイル $L$ は短絡されているのと同じということになります。(これ、大事!)

ちなみに、RL直列回路の時定数 $\tau$ は、$\tau = \dfrac{L}{R}$ になります。
時定数については、こちらの時定数のページを参考にしてみてください。
スポンサーリンク
スポンサーリンク
RL直列回路の抵抗Rの電圧の求め方
RL直列回路に流れる電流 $i(t)$ はさきほどの⑪式で与えられるので、⑪式を使うと、抵抗 $R$ にかかる電圧 $e_R(t)$[$ \mathrm{V} $]は次のようになります。
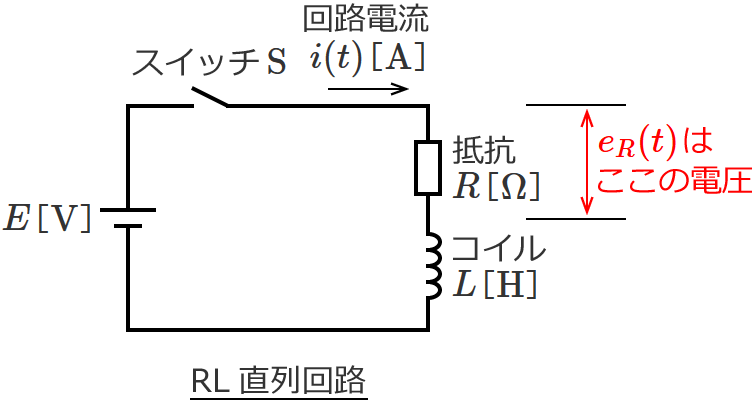
$e_R(t) = i(t) \cdot R$
$= \left( \dfrac{E}{R} - \dfrac{E}{R} \cdot e^{-\frac{R}{L} t} \right) \cdot R$
$= E - E \cdot e^{-\frac{R}{L} t}$
$\therefore e_R(t) = E - E \cdot e^{-\frac{R}{L} t}$ …⑫ (これが抵抗 $R$ の電圧)
電流を求めてしまえば、抵抗 $R$ の電圧は簡単に求められますね。
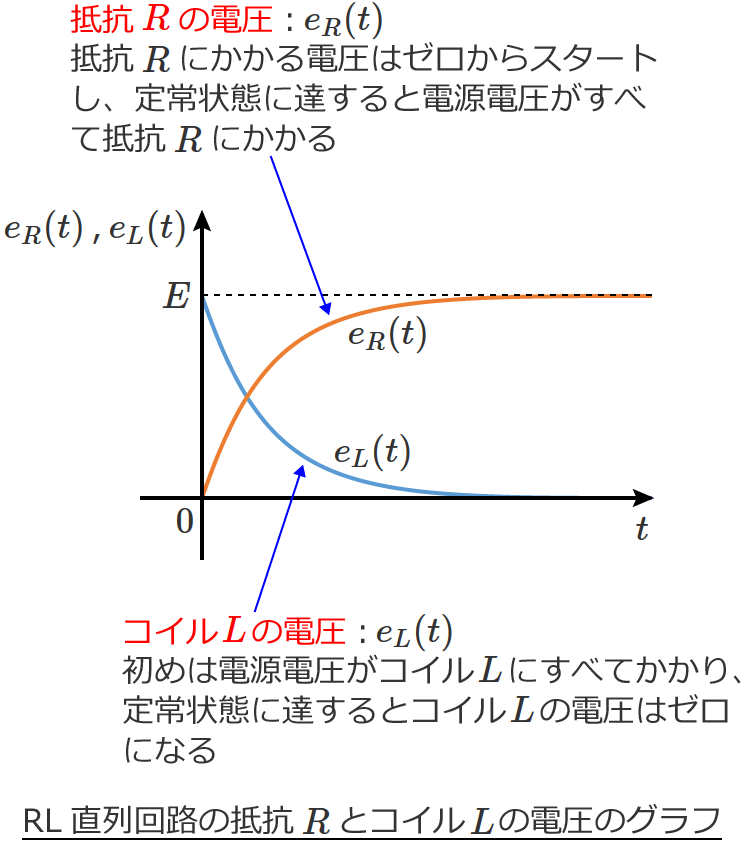
RL直列回路の抵抗Rの電圧のグラフ
グラフについては、電圧 $e_R(t)$ は $i(t)$ に $R$ をかけただけなので、$i(t)$ と同じような形のグラフになります。
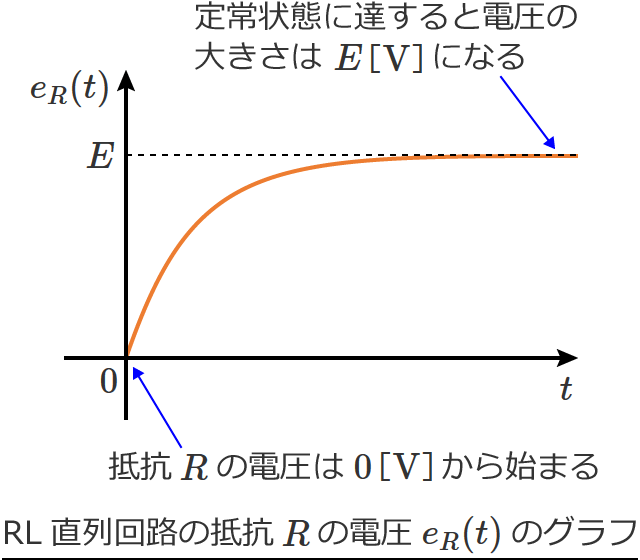
このグラフをみると、抵抗 $R$ の電圧は $0$[$ \mathrm{V} $]から始まり、ある程度時間が経過する(定常状態に達するという意味)と電圧の大きさは $E$[$ \mathrm{V} $]になるのが分かります。
抵抗 $R$ の電圧 $e_R(t)$ が最終的に $E$[$ \mathrm{V} $]になるということは、電源の電圧がすべて抵抗 $R$ にかかることになるということです。
つまり、定常状態に達するとコイル $L$ が無いのと同じ(コイルが短絡された状態と同じ)ということになります。(これ、大事!)
RL直列回路のコイルLの電圧の求め方
コイル $L$ の電圧についても求めてみましょう。
ここでもさきほど求めた電流 $i(t)$ の式(⑪式)を使うと、コイル $L$ の電圧 $e_L(t)$[$ \mathrm{V} $]は次のようになります。
$e_L(t) = L \dfrac{d \, i(t)}{dt}$
$= L \dfrac{d}{dt} \left( \dfrac{E}{R} - \dfrac{E}{R} \cdot e^{-\frac{R}{L} t} \right)$
この式を解くとコイル $L$ の電圧 $e_L(t)$ を求めることができます。では、解いてみましょう。
$\dfrac{E}{R}$ は定数なので、微分の外に出してしまいます。
$e_L(t) = \dfrac{LE}{R} \cdot \dfrac{d}{dt} \left( 1 - e^{-\frac{R}{L} t} \right)$
$=\dfrac{LE}{R}\left( \dfrac{d}{dt} 1-\dfrac{d}{dt} e^{-\frac{R}{L} t}\right)$
$=\dfrac{LE}{R} \left\lbrace 0 - \left( -\dfrac{R}{L} \cdot e^{-\frac{R}{L} t} \right) \right\rbrace$
$= \dfrac{LE}{R} \left( \dfrac{R}{L} \cdot e^{-\frac{R}{L} t} \right)$
$= E \cdot e^{-\frac{R}{L} t}$
$\therefore e_L(t) = E \cdot e^{-\frac{R}{L} t}$ …⑬ (これがコイル $L$ の電圧)
以上でRL直列回路のコイル $L$ の電圧 $e_L(t)$ が求められました。
RL直列回路のコイルLの電圧のグラフ
コイル $L$ の電圧 $e_L(t)$ が求められたのでグラフも書いてみます。
さきほど求めた電圧の式(⑬式)より、コイル $L$ の電圧の式は次のようになります。
$e_L(t) = E \cdot e^{-\frac{R}{L} t}$ …⑬
⑬式より、コイル $L$ の電圧 $e_L(t)$ の $t=0$ および $t=\infty$ での値をそれぞれ求めると、
$t=0$ のとき
$e_L(0)=E\cdot e^{-\frac{R}{L}\times 0}$ (⑬式の $t$ に $0$ を代入した)
$=E\cdot e^0$
$=E\times 1=E$
$\therefore$ $t=0$ のとき $E$
$t=\infty$ のとき
$e_L(\infty )=E\cdot e^{-\frac{R}{L}\times\infty}$ (⑬式の $t$ に $\infty$ を代入した)
$=E\cdot\dfrac{1}{e^{\frac{R}{L}\times\infty}}$
$=E\cdot\dfrac{1}{\infty} =0$
$\therefore$ $t=\infty$ のとき $0$
となります。
また、⑬式は $e^{-\frac{R}{L} t}$ によって減衰していくので、コイル $L$ の電圧 $e_L(t)$ のグラフは、時間がたつにつれて減少がゆるやかになる次のようなグラフになります。
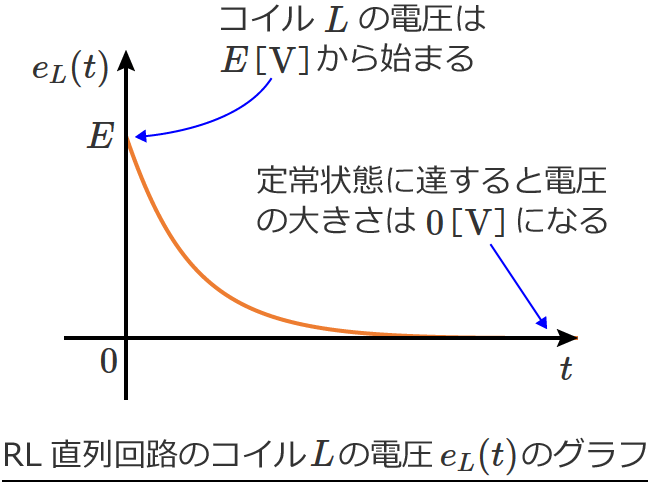
このグラフをみると、コイル $L$ の電圧は $E$[$ \mathrm{V} $]から始まり、ある程度時間が経過する(定常状態に達するという意味)と電圧の大きさは $0$[$ \mathrm{V} $]になるのが分かります。
つまり、スイッチをONした直後は電源の電圧がすべてコイル $L$ にかかりますが、定常状態に達するとコイル $L$ には電圧がかからず、電源の電圧はすべて抵抗 $R$ にかかるということになります。(これ、大事!)
RL直列回路の過渡現象のまとめ
以上をまとめると次のようになります。
RL直列回路
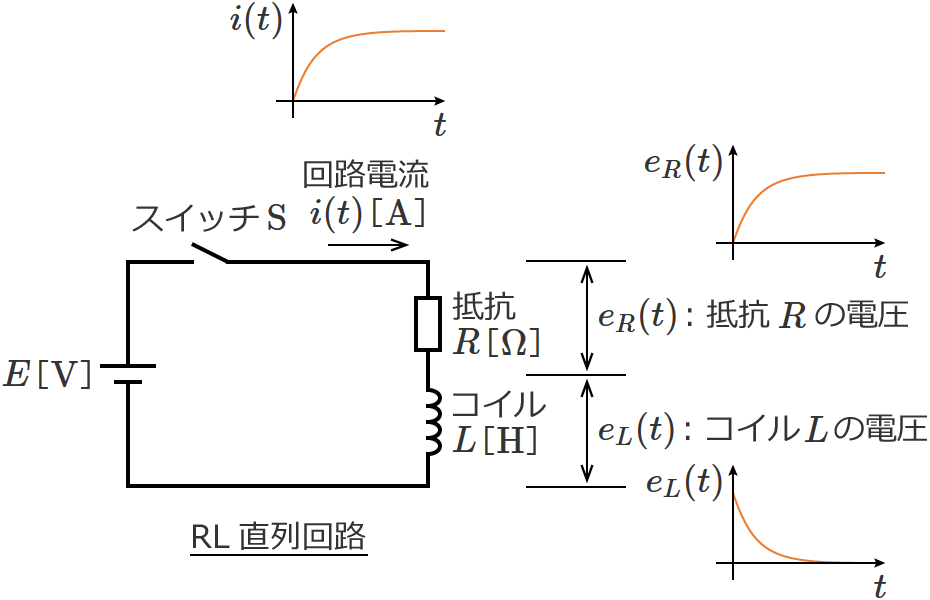
RL直列回路の過渡現象の解き方
❶回路の回路方程式(微分方程式)をたてる
❷初期条件を使って❶の微分方程式を解いて電流を求める
❸電圧は❷で求めた電流を使って求める
RL直列回路の過渡現象の式
回路に流れる電流: $i(t) = \dfrac{E}{R} - \dfrac{E}{R} \cdot e^{-\frac{R}{L} t}$
抵抗 $R$ の電圧: $e_R(t) = E - E \cdot e^{-\frac{R}{L} t}$
コイル $L$ の電圧: $e_L(t) = E \cdot e^{-\frac{R}{L} t}$
RL直列回路の時定数
時定数: $\tau = \dfrac{L}{R}$
RL直列回路の過渡現象のグラフ
<電流のグラフ>
<電圧のグラフ>
過渡現象を解くためには微分方程式(または積分方程式)を解く必要があるため計算が大変になる場合もありますが、たいていの場合、決まった形の微分方程式を解くだけなので、初めは大変かもしれませんがパターンをおぼえて慣れれば大丈夫ですよ。
それから、電験二種の一次試験の理論では過渡現象の解き方などが出題されることがあり、RL直列回路とRC直列回路の過渡現象の解き方は過渡現象回路を解くための基本になるので、電験二種を受験する方は解き方をおぼえておくようにしましょう。
電験三種を受験する方は過渡現象の解き方までは分からなくてもいいと思いますが、RL直列回路とRC直列回路の過渡現象のグラフと時定数は必ずおぼえておくようにしましょう。
スポンサーリンク
スポンサーリンク
そもそも過渡現象ってなんでしたっけ?という方は、こちらの過渡現象とはのページを参考にしてみてください。
RC直列回路については、こちらのRC直列回路の過渡現象の解き方のページを参考にしてみてください。
ラプラス変換を使ったRL直列回路の過渡現象の解き方については、こちらのラプラス変換によるRL直列回路の過渡現象の解き方のページを参考にしてみてください。
RC直列回路の時定数(τ=CR)の導出 ←BACK
NEXT→ RC直列回路の過渡現象の解き方
スポンサーリンク
RL直列回路の過渡現象の解き方 関連ページ
- 過渡現象とは
- 過渡現象について解説しています。過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象(電圧や電流などの時間的な変化)のことをいい、過渡現象は回路の状態が変化することによって起こります。
- 時定数
- 過渡現象の時定数について解説しています。時定数は、過渡状態での変化の速さを表わす量で、時定数が小さければ変化する速さは速くなり、時定数が大きければ変化する速さは遅くなります。
- 時定数の単位はなぜ時間s(秒)になるのか?
- 過渡現象の時定数の単位はなぜ時間s(秒)になるのか?について解説しています。時定数の単位が時間(s)になる過程も詳しく書いていますので、参考にしてみてください。
- RL直列回路の時定数(τ=L/R)の導出
- RL直列回路の時定数(τ=L/R)の導出方法について解説しています。RL直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の時定数(τ=CR)の導出
- RC直列回路の時定数(τ=CR)の導出方法について解説しています。RC直列回路の時定数は、電流のt=0における接線と定常状態の電流を表わす直線との交点の時間を算出すると求められます。
- RC直列回路の過渡現象の解き方
- RC直列回路の過渡現象の解き方について解説しています。RC直列回路の過渡現象はRL直列回路よりもちょっとだけ計算が大変ですが、解き方のパターンは同じなので、おぼえてしまうとそれほど難しくはありませんよ。
- ラプラス変換によるRL直列回路の過渡現象の解き方
- ラプラス変換によるRL直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRL直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。
- ラプラス変換によるRC直列回路の過渡現象の解き方
- ラプラス変換によるRC直列回路の過渡現象の解き方について解説しています。ラプラス変換を使ってRC直列回路の過渡現象を解いていますので、ラプラス変換を使った過渡現象の解き方の参考にしてみてください。


