電気のお勉強｜電気磁気学｜クーロンの法則

スポンサーリンク

クーロンの法則は、電気というか電気磁気学の分野ですご〜く有名な法則で、

 

電荷間に働く力（反発または引き合う力）は電荷の積に比例し、電荷間の距離の2乗に反比例します

 

という法則です。

 

電荷？？　働く力？？

 

ここでは、クーロンの法則をできるだけ簡単に理解しやすいように、電荷のイメージから説明します。

 

クーロンの法則の公式を暗記してしまうだけでもいいのですが、式だけではなく、その法則のイメージを持っておくことは大事です。イメージを持っておくと忘れにくくなり、理解度も深まりますよ。

 

スポンサーリンク

 

クーロンの法則（電荷のイメージ）

クーロンの法則は電荷についての法則なので、まずは電荷のイメージです。

 

電荷？？

 

電荷は「電気のかたまり」みたいなものとイメージしておけばいいです。

 

それで、電気にはプラスとマイナスがありますが、電荷は電気のかたまりなので、電荷にもプラスとマイナスがあります。

 

電荷を絵で書くときは、たいていの場合、プラスの電荷は「○に＋」、マイナスの電荷は「○に−」で書きます。

 

 

電荷にはプラスとマイナスの電荷がありますが、これらを近くに置いてみたらどうなっちゃうんでしょうか？

 

とりあえず、プラスの電荷の近くにプラスの電荷をもう1つ置いてみますか。

 

 

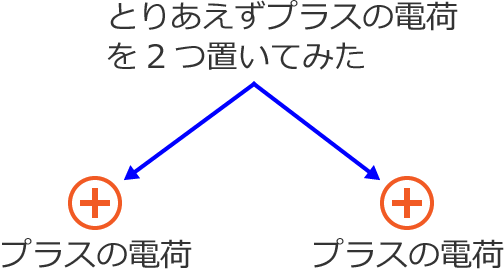
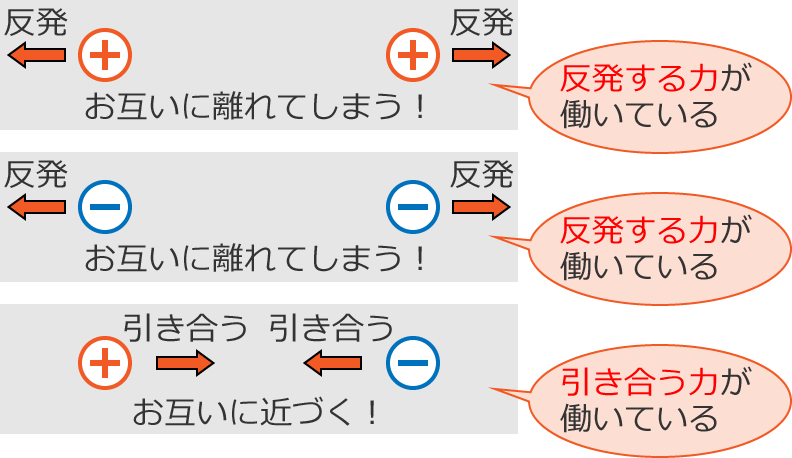
そうすると、磁石のN極とN極が反発し合うように、電荷も同じ種類（プラスとかマイナスという意味）どうしのときには、お互いに反発して離れてしまいます。

 

 

マイナスとマイナスの場合も、同じ種類の電荷なので離れてしまいます。

 

 

次は、プラスの電荷の近くにマイナスの電荷を置いてみますか？

 

だいたい想像できますね。

 

 

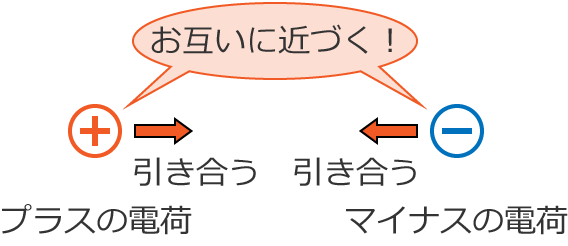
プラスとマイナスの場合は、磁石のN極とS極が引き合うように、電荷も違う種類のときはお互いに引き合って近づきます。

 

以上の3パターン（プラスとプラス、マイナスとマイナス、プラスとマイナス）から、2つの電荷には反発する力または引き合う力が働くことが分かりました。

 

それから、電荷には大きさ（量）があり、その大きさを電荷量といいます。電荷量が大きい場合は電気がいっぱい！電荷量が小さい場合は電気が少し、そんな感じです。

 

また、電荷量の単位は［$ \mathrm{C} $］で、［$ \mathrm{C} $］は「クーロン」と読みます。電荷量を書くときは一般的にアルファベットの「$Q$ または $q$」が使われるので、電荷量を単位も含めて書くと、$Q$［$ \mathrm{C} $］、こんな感じになります。

 

クーロンの法則を理解するために電荷についておぼえておくことはこんなところです。

 

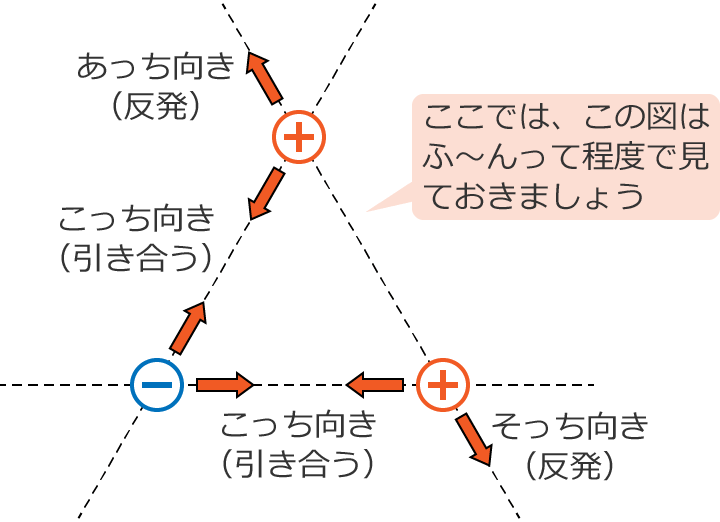
あ、それから、2つの電荷がお互いに「反発する向き」または「引き合う向き」（つまり、2つの電荷に働く力の向き）は、2つの電荷を結んだ直線上になります。

 

 

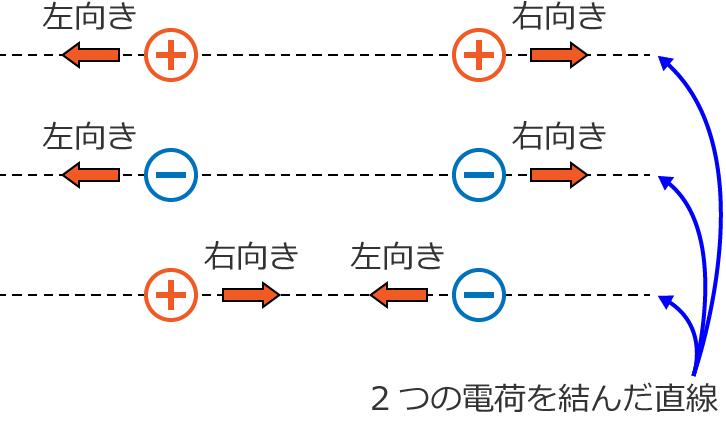
そりゃそうだ！って思うかもしれませんが、これってものすごく大事なことなのでおぼえておきましょう。ここでは電荷が2つだけの場合で説明しましたが、電荷が3つとか4つのときの場合を考えるときにとても大事な考え方になります。

 

 

 

クーロンの法則（ここからが本題）

それでは、ここからが本題です。

 

電荷のイメージができれば、あとは簡単です。たぶん。

 

もう一度クーロンの法則について書くと、クーロンの法則とは、

 

電荷間に働く力（反発または引き合う力）は電荷の積に比例し、電荷間の距離の2乗に反比例します

 

でした。

 

この文章を次の①〜③に分解して考えてみましょう。

 

 

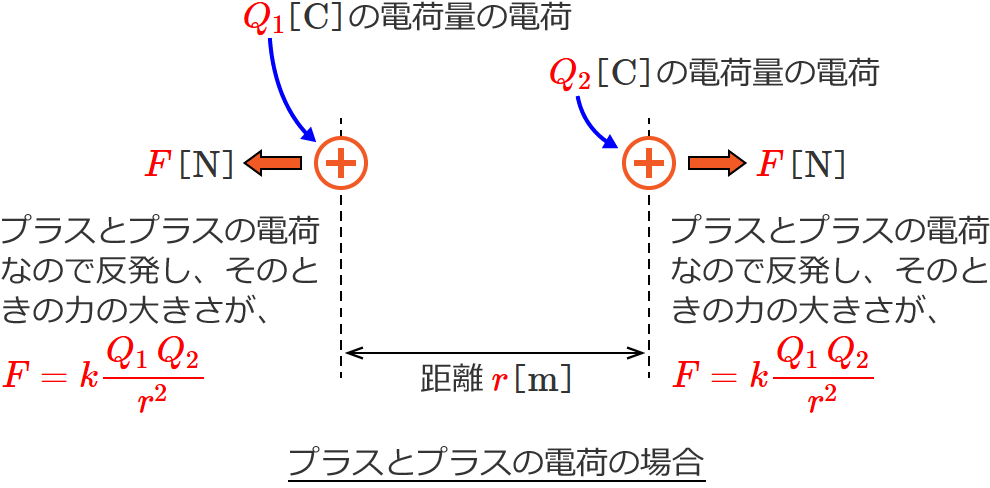
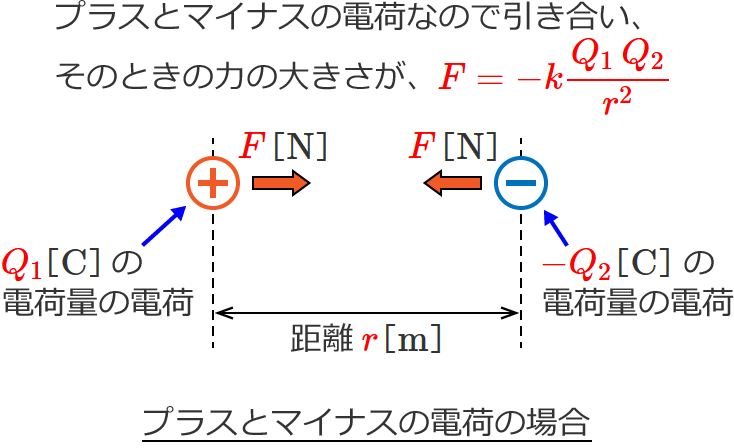
電荷のイメージのところで書いたように、プラスとプラスの電荷は反発し、マイナスとマイナスの電荷も反発し、プラスとマイナスの電荷は引き合います。このときの反発する力、引き合う力が「電荷間に働く力」です。

 

 

電荷の積の「電荷」は電荷量のことなので、「電荷の積」は2つの電荷量をかけたものということになります。

 

 

電荷間の距離はそのままの意味で、電荷と電荷の間の距離になります。

 

 

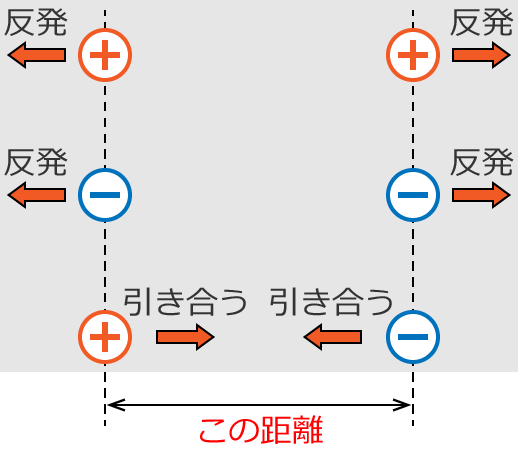
すると、①〜③より、クーロンの法則をもうちょっと分かりやすく書くと次のようになります。

 

2つの電荷が反発または引き合う力は、2つの電荷の電荷量をかけたものに比例し、2つの電荷間の距離を2乗したものに反比例します

 

あまり変わっていないような気もしますが…
ちょっとは分かりやすくなってますか？　ほぼ同じか…。

 

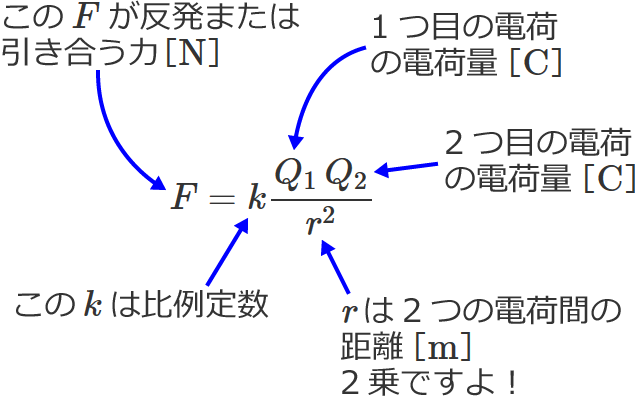
これを式で書いたのがクーロンの法則の公式で、次のような式になります。

 

$F = k \dfrac{Q_1 \, Q_2}{r^2}$　［$ \mathrm{N} $］

 

この式の各値についてちょっと説明すると、

 

$F$ ：2つの電荷が反発または引き合う力、単位は［$ \mathrm{N} $］（ニュートンと読みます）
$Q_1$ ：1つ目の電荷の電荷量、単位は［$ \mathrm{C} $］
$Q_2$ ：2つ目の電荷の電荷量、単位は［$ \mathrm{C} $］
$r$ ：2つの電荷間の距離、単位は［$ \mathrm{m} $］
$k$ ：比例定数で、$k = \dfrac{1}{4 \pi \varepsilon_0} \fallingdotseq 9 \times 10^9$［$ \mathrm{N \cdot m^2 / C^2} $］という値になります。（$\varepsilon_0$ は真空の誘電率）

 

図で書いてみると、

 

 

となります。

 

このクーロンの法則の公式を、先ほどでてきた図と対応させてみましょう。

 

まず、プラスとプラスの電荷の場合は、こんな感じです。

 

 

次に、プラスとマイナスの電荷の場合は、こんな感じです。

 

 

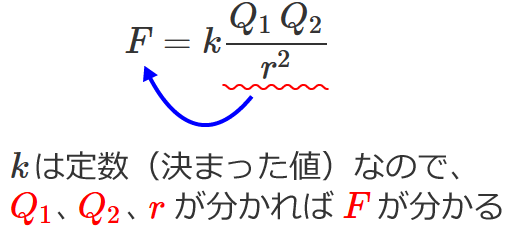
上の図をみていると、クーロンの法則の公式の意味が分かってきますね！　どういう意味？？

 

クーロンの法則は、

 

2つの電荷の電荷量と電荷間の距離が分かると、2つの電荷が反発または引き合う力の大きさが分かる

 

という法則だったんですね！

 

 

 

クーロンの法則のまとめ

以上、クーロンの法則をまとめると次のようになります。

 

 

 

電気のお勉強のＴＯＰ　←BACK

NEXT→　右ねじの法則

スポンサーリンク

クーロンの法則　関連ページ

右ねじの法則

電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き（方向）の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。

ビオ・サバールの法則

電気磁気学の「ビオ・サバールの法則」とその法則を使った磁界の計算方法について解説しています。直線状電流の磁界の計算方法や円形コイル電流の磁界の計算方法はビオ・サバールの法則の使い方の基本になりますので、おぼえておくようにしましょう。

フレミングの左手の法則と右手の法則

「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。

電界中の電子の運動

電界中の電子の運動について解説しています。電界中に電子を置いたときや、電界に電子が突入したときの電子の運動について解説していますので、電界中の電子の運動の勉強の参考にしてみてください。

電界中の電子のエネルギーと電子が陽極に達したときの速度

電界中の電子のエネルギーと電子が陽極に達したときの速度について解説しています。電界中の電子の位置エネルギーや運動エネルギーなどについて解説していますので、電界中の電子のエネルギーの勉強の参考にしてみてください。

ローレンツ力

ローレンツ力について解説しています。ローレンツ力の力の向きや大きさの求め方、円運動などについても解説していますので、ローレンツ力の勉強の参考にしてみてください。

電磁誘導

電気磁気学の「電磁誘導」と「電磁誘導に関するファラデーの法則」について解説しています。電磁誘導は、コイルを貫く磁束が変化するとコイルに起電力（誘導起電力）が発生する現象です。

レンツの法則

電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。