スポンサーリンク
ビオ・サバールの法則とは?
※ページ内にPR・広告が含まれる場合があります。
ビオ・サバールの法則は電気磁気学の法則で、
電線に流れる電流によって作られる磁界の大きさ(強さ)を求めるときなどに使われる法則
です。
例えば、次の図のように直線状の電線や円形状の電線に電流が流れているとしますよね?
このときに、ある点に作られる磁界の大きさはいくら?
というときにビオ・サバールの法則を使うと、ある点に作られる磁界の大きさを求めることができます。
それでビオ・サバールの法則ですが、例えば次の図のようなフニャっとした電線に電流 $I$ が流れていて、電線の微小部分を $dl$、$dl$ の方向(電線の接線方向)と $dl$ から点 $\mathrm{P}$ を見たときの方向とのなす角を $\theta$、$dl$ と点 $\mathrm{P}$ との距離を $r$ とすると、微小部分 $dl$ により点 $\mathrm{P}$ に作られる磁界の大きさは、
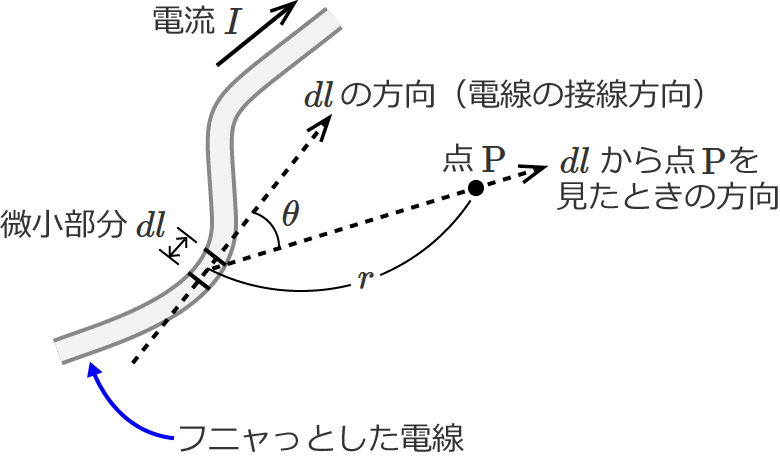
$dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ [$ \mathrm{A / m} $] …① (←これがビオ・サバールの法則の式)
で与えられるという法則です。
簡単に言えば、「ビオ・サバールの法則を使うと、電流が流れている電線の周りの磁界を求めることができます。」ってことですね。
このビオ・サバールの法則の式を使うと任意の点 $\mathrm{P}$ の磁界の大きさを求めることができるのですが、ここでちょっと注意です!
①式をみると、左辺は「$dH$」と書かれていますよね?
これは、微小部分 $dl$ だけによる磁界の大きさという意味で、つまり、電線に流れている電流全体によって作られる磁界の大きさではありません。
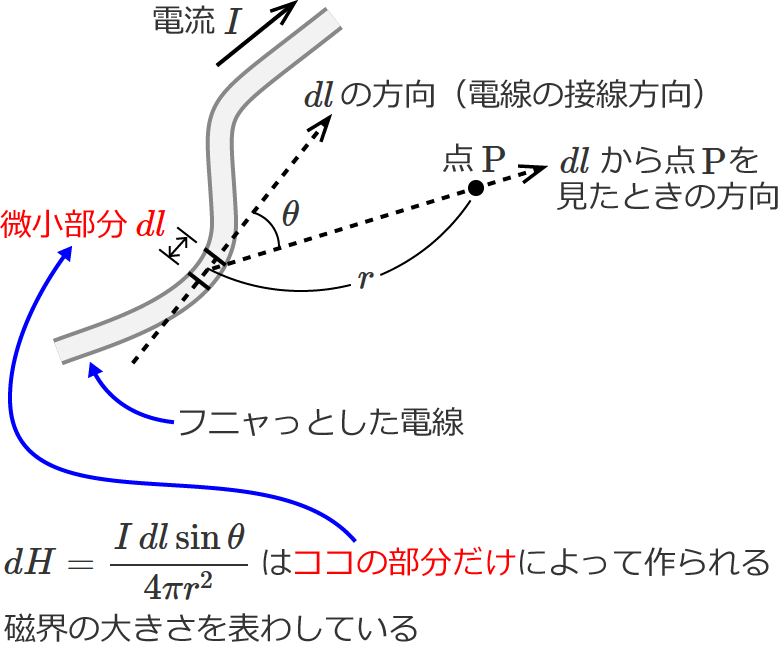
なので、電線に流れる電流全体によって作られる点 $\mathrm{P}$ の磁界の大きさを求めるためには、
(微小部分 $dl$ が点 $\mathrm{P}$ に作る磁界)+(微小部分 $dl$ が点 $\mathrm{P}$ に作る磁界)+(微小部分 $dl$ が点 $\mathrm{P}$ に作る磁界)+・・・
と、足し合わせていく必要があります。つまり、こういうことです。
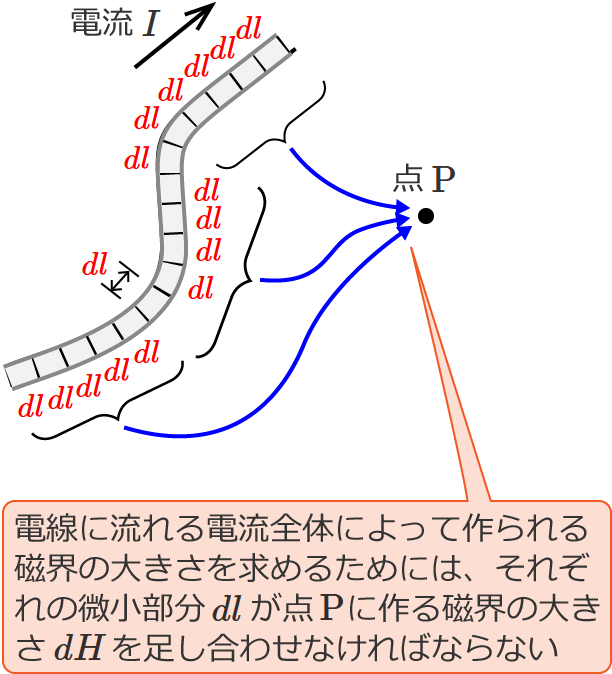
この足し合わせる計算を一つ一つしていったら大変ですよね? 電線が無限の長さだったら無限に計算が続いてしまいます。計算が終わりません!
こんな計算のときには積分が役に立ちますね!
①式の両辺を積分してみましょう。①式の両辺を積分すると、
$\displaystyle\int dH = \int \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ 、 $\displaystyle\int dH = H = \int \dfrac{I \sin \theta}{4 \pi r^2} \, dl$
$\therefore H = \displaystyle\int \dfrac{I \sin \theta}{4 \pi r^2} \, dl$ [$ \mathrm{A / m} $] …② となります。
この②式には積分範囲(積分する範囲)が書いていなくて不定積分の形になっていますが、積分範囲は求めたい電線(電流)の形状などを考慮して与えればいいです。
これなら無限に計算をする必要がないですね!
では次に、このビオ・サバールの法則を使って、無限直線状電流による磁界の大きさ、円形コイル電流による磁界の大きさを求めてみることにしましょう。
スポンサーリンク
ビオ・サバールの法則による無限直線状電流の磁界の大きさの求め方
まず初めに、ここでの無限直線状電流について説明します。
無限直線状電流とは、無限に長く続く直線に流れる電流という意味で、次の図のようなものです。
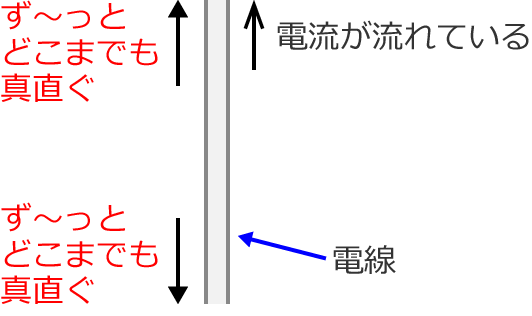
どこまでもず〜っと真直ぐな電線に流れている電流ということですね。説明ってほどでもありませんが、こんな電流です。
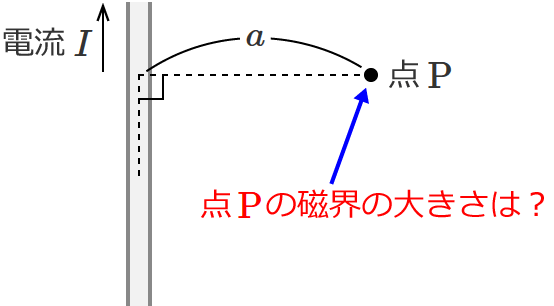
それで、この無限直線状電流から距離 $a$ 離れた一点を点 $\mathrm{P}$ としたとき、
点 P の磁界の大きさはいくらでしょうか?
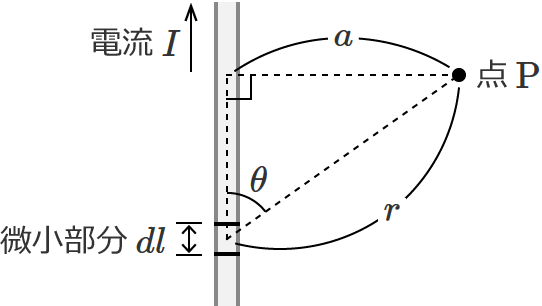
電線の微小部分を $dl$、$dl$ の方向(電線の接線方向)と $dl$ から点 $\mathrm{P}$ を見たときの方向とのなす角を $\theta$、$dl$ と点 $\mathrm{P}$ との距離を $r$ として図を書くと次のようになりますね。
ビオ・サバールの式(①式)は、こんな式でした。
$dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ …①
この①式と上図を見比べてみると、電線に流れる電流は $I$、微小部分は $dl$、$dl$ の方向(電線の接線方向)と $dl$ から点 $\mathrm{P}$ を見たときの方向とのなす角は $\theta$、$dl$ と点 $\mathrm{P}$ との距離は $r \cdots$
あ、そのまんま①式を使えますね。なので、微小部分 $dl$ だけによる磁界の大きさ $dH$ は、
$dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ …③ となります。
ここで、先ほど「注意」として書いたように、$dH$ は $dl$ だけによる磁界の大きさでした。
今求めたい磁界の大きさは、無限に長い直線状電流によって作られる磁界の大きさなので、③式を足し合わせ(積分)しなければなりませんね。
積分範囲は、直線状の電流が無限に長く続いているので、$- \infty$ から $+ \infty$ となります。
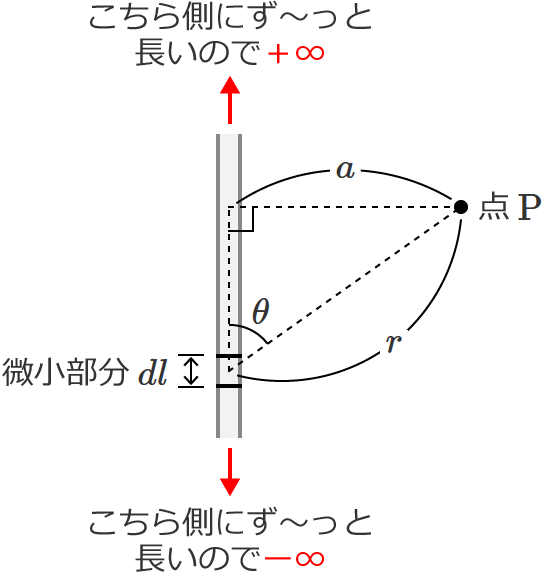
したがって、③式を $- \infty$ から $+ \infty$ の範囲で積分すればいいです。なので③式より、
$H = \displaystyle\int_{- \infty}^{+ \infty} \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ $= \displaystyle\int_{- \infty}^{+ \infty} \dfrac{I \sin \theta}{4 \pi r^2} \, dl$
$4 \pi$ と $I$ は定数なので、積分の外に出しましょう。
$H = \dfrac{I}{4 \pi} \displaystyle\int_{- \infty}^{+ \infty} \dfrac{\sin \theta}{r^2} \, dl$ …④
④式をみると、あらら困りました…。$l$ で積分する式になっているのですが、積分の中の式は変数 $\theta$ と $r$ になっています。このままでは積分できないので、④式を定数 $a$ と $\theta$ の式に変形します。
点 $\mathrm{P}$ から直線状電線に垂直にひいた線分と直線状電線との交点を原点として座標を考えると、次のようになりますね。
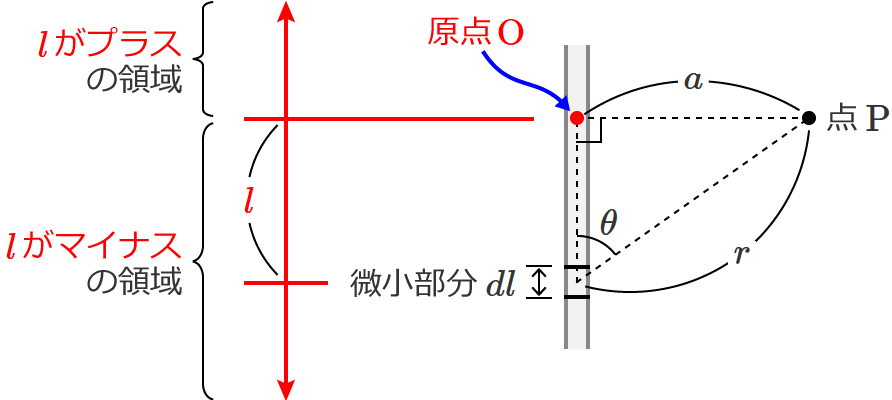
この図より、$a = r \sin \theta$ …⑤ $l = - r \cos \theta$ …⑥ が成り立ちます。(⑥式は上図よりマイナスが付くことに注意しましょう。)
⑤式より、$r = \dfrac{a}{\sin \theta}$ …⑦
⑦式を⑥式に代入すると、$l = -\dfrac{a}{\sin \theta} \cdot \cos \theta$ $\therefore l = -\dfrac{a \cos \theta}{\sin \theta}$ …⑧
⑧式を $\theta$ で微分します。すると、
$\dfrac{dl}{d \theta}$ $= - \left( \dfrac{-a \sin \theta \cdot \sin \theta - a \cos \theta \cdot \cos \theta}{\sin^2 \theta} \right)$ (←微分の公式を使っています)
$= \dfrac{a \sin^2 \theta + a \cos^2 \theta}{\sin^2 \theta}$ $= \dfrac{a ( \sin^2 \theta + \cos^2 \theta )}{\sin^2 \theta}$ $= \dfrac{a}{\sin^2 \theta}$ $\left( \because \sin^2 \theta + \cos^2 \theta = 1 \right)$
$\therefore dl = \dfrac{a}{\sin^2 \theta} \, d \theta$ …⑨
⑦、⑨式を④式に代入すると $\theta$ の式になりますが、$l$ の式から $\theta$ の式に変換しているので④式の積分範囲が変わります。
④式は $l$ で積分する式で、積分範囲が $-\infty$ から $+\infty$ ですが、これを $\theta$ で考えた場合の積分範囲は $0$ から $+ \pi$ になります。
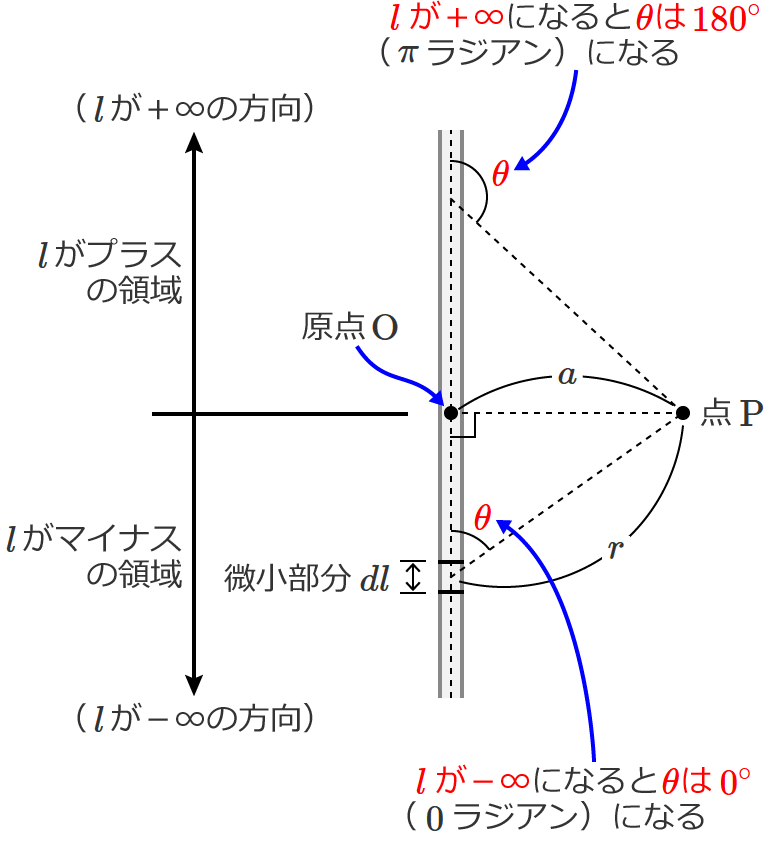
したがって、⑦、⑨を④式に代入して積分範囲を $\theta$ で考えると、
$H = \dfrac{I}{4 \pi} \displaystyle\int_{-\infty}^{+\infty} \dfrac{\sin \theta}{r^2} \, dl$ $= \dfrac{I}{4 \pi} \displaystyle\int_0^\pi \dfrac{1}{\left( \dfrac{a}{\sin \theta} \right)^2} \cdot \sin \theta \cdot \dfrac{a}{\sin^2 \theta} \, d \theta$
あとは、これを計算していけば、求めたい無限直線状電流によって作られる磁界の大きさが求められます。
$H$ $= \dfrac{I}{4 \pi} \displaystyle\int_0^\pi \dfrac{1}{\dfrac{a^2}{\sin^2 \theta}} \cdot \sin \theta \cdot \dfrac{a}{\sin^2 \theta} \, d \theta$ $= \dfrac{I}{4 \pi} \displaystyle\int_0^\pi \dfrac{\sin^2 \theta}{a^2} \cdot \sin \theta \cdot \dfrac{a}{\sin^2 \theta} \, d \theta$
$= \dfrac{I}{4 \pi} \displaystyle\int_0^\pi \dfrac{\sin \theta}{a} \, d \theta$ $= \dfrac{I}{4 \pi a} \displaystyle\int_0^\pi \sin \theta \, d \theta$ $= \dfrac{I}{4 \pi a} \left[ -\cos \theta \right]_0^\pi$ $= \dfrac{I}{4 \pi a} ( -\cos \pi + \cos 0 )$
$= \dfrac{I}{4 \pi a} ( 1+1 ) = \dfrac{I}{4 \pi a} \cdot 2 = \dfrac{I}{2 \pi a}$
したがって、無限直線状電流による磁界の大きさは、
$\therefore H = \dfrac{I}{2 \pi a}$ [$ \mathrm{A / m} $]
となります。
$l$ ⇒ $\theta$ に変換する計算方法について
$l$ ⇒ $\theta$ に変換する計算過程において、参考書によっては $\cot \theta$ や $\mathrm{cosec} \, \theta$ を使って表わしていますが、このページの計算方法のように $\sin \theta$ 、$\cos \theta$ だけでも表わす(計算する)ことができます。
「$\cot \theta$ や $\mathrm{cosec} \, \theta$ は苦手だな〜」という方は、このページの計算方法で計算した方が比較的おぼえやすく簡単かもですよ。
スポンサーリンク
スポンサーリンク
ビオ・サバールの法則による円形コイル電流の磁界の大きさの求め方
次は、円形コイルに流れる電流(ループ電流)により作られる磁界の大きさをビオ・サバールの法則により求めてみます。
円形コイルは次のような円形の電線で、この円形コイルを電流がぐるぐる流れています。
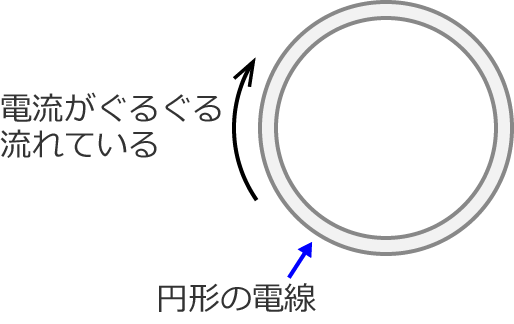
この円形コイルの中心の磁界の大きさはいくらでしょうか?
円形コイルの中心を点 $\mathrm{O}$、円形コイルの微小部分を $dl$、円形コイルの中心軸上の任意の点を点 $\mathrm{P}$、線分 $\mathrm{OP}$ の方向と $dl$ から点 $\mathrm{P}$ を見たときの方向とのなす角を $\phi$、$dl$ と点 $\mathrm{P}$ との距離を $r$ として図を書くと次のようになりますね。
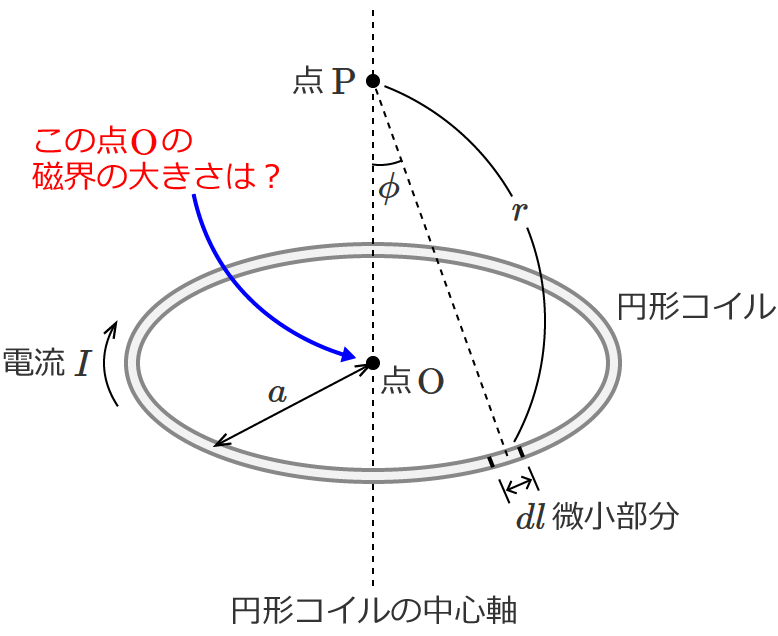
求める磁界の大きさは点 $\mathrm{O}$ の磁界の大きさですが、まず点 $\mathrm{P}$ の磁界の大きさを求めて、そのあとに条件を代入して点 $\mathrm{O}$ の磁界の大きさを求めます。
では、点 $\mathrm{P}$ の磁界の大きさを求めてみましょう。ビオ・サバールの法則の式(①式)は、こんな式でした。
$dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2}$ …①
この①式と上図を見比べてみると、円形コイルに流れる電流は $I$、微小部分は $dl$、$dl$ と点 $\mathrm{P}$ との距離は $r$ ですね。
ここで一つ気を付けなければならないのは、①式の角度 $\theta$ は上図の角度 $\phi$ ではなく、$dl$ の方向(電線の接線方向)と $dl$ から点 $\mathrm{P}$ を見たときの方向とのなす角です。
なので、この場合には $\theta = 90^{\circ}$ となり、①式の $\sin \theta$ は $\sin \theta = 1$ になります。
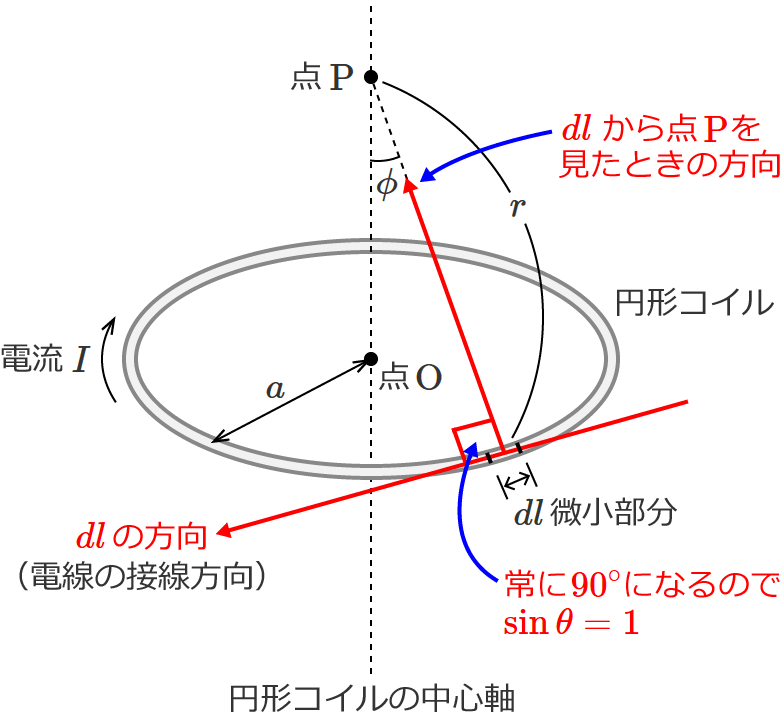
したがって、微小部分 $dl$ による磁界の大きさ $dH$ は、
$dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2} = \dfrac{I \, dl}{4 \pi r^2}$ $\therefore dH = \dfrac{I \, dl}{4 \pi r^2}$ …⑩ となります。
ここで、点 $\mathrm{P}$ に作られる磁界について考えてみましょう。上図を横から見ると次のようになります。(横から見たときの点 $\mathrm{P}$ の横方向を $x$ 方向、縦方向を $y$ 方向としています。)
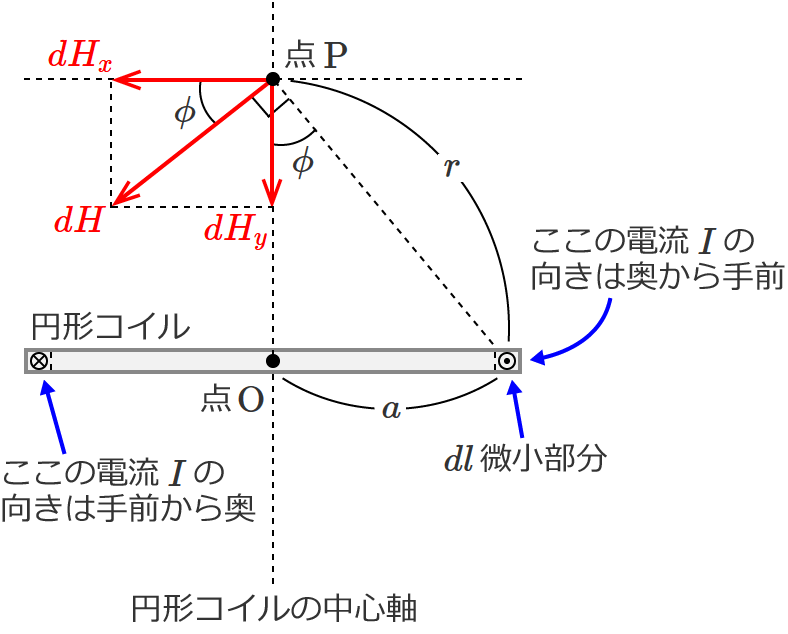
この図より $dH$ の $x$ 成分 $dH_x$ は、微小部分 $dl$ がぐるっと一周すると全て打ち消しあってゼロになります。
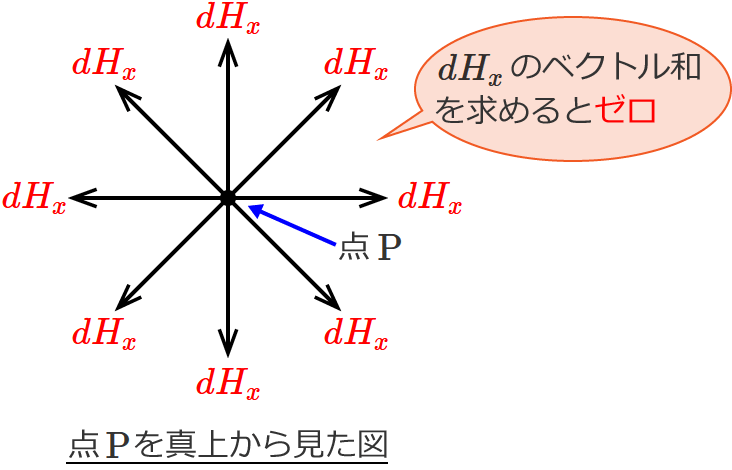
なので、この場合には $y$ 方向成分だけ考えればいいことになります。$y$ 方向成分 $dH_y$ は図より、
$dH_y = dH \sin \phi$ …⑪ となります。
この⑪式に⑩を代入すると、$dH_y = \dfrac{I \, dl}{4 \pi r^2} \sin \phi$ となり、これを円形コイルのぐるっと一周分足し合わせたものを求めればいいです。この場合は円形コイルなので、円の円周分($2 \pi a$)足し合わせればいいですね。
なので、積分範囲を $0$ から $2 \pi a$ とすると円形コイル電流による磁界の大きさの式は次のようになります。
$H_y = H = \displaystyle\int_0^{2 \pi a} \dfrac{I \, dl}{4 \pi r^2} \sin \phi$ $\therefore H = \displaystyle\int_0^{2 \pi a} \dfrac{I \sin \phi}{4 \pi r^2} \, dl$ …⑫
($x$ 成分 $H_x$ は考えなくていいので、$y$ 成分 $H_y$ が求める $H$ になります。)
あとは⑫式を計算するだけですが、ここで、次の図のように円形コイルの中心 $\mathrm{O}$ を原点とする座標を考えます。
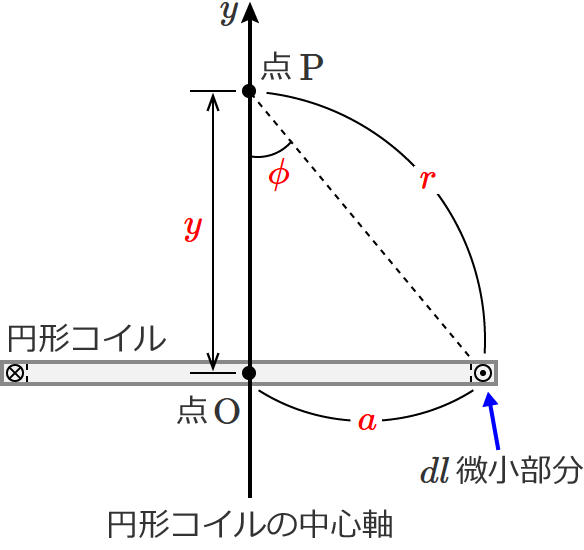
すると、$r = \sqrt{a^2 + y^2}$ 、 $\sin \phi = \dfrac{a}{r} = \dfrac{a}{\sqrt{a^2 + y^2}}$ が成り立つので、これらを⑫式に代入します。
$H = \displaystyle\int_0^{2 \pi a} \dfrac{I \sin \phi}{4 \pi r^2} \, dl$ $= \displaystyle\int_0^{2 \pi a} \dfrac{I}{4 \pi \left( \sqrt{a^2 + y^2 } \right)^2} \cdot \dfrac{a}{\sqrt{a^2 + y^2}} \, dl$
$= \displaystyle\int_0^{2 \pi a} \dfrac{aI}{4 \pi \left( a^2 + y^2 \right)^{\frac{3}{2}}} \, dl$ $= \dfrac{aI}{4 \pi \left( a^2 + y^2 \right)^{\frac{3}{2}}} \displaystyle\int_0^{2 \pi a} dl$ $= \dfrac{aI}{4 \pi \left( a^2 + y^2 \right)^{\frac{3}{2}}} \left[ l \right]_0^{2 \pi a}$
$= \dfrac{aI}{4 \pi \left( a^2 + y^2 \right)^{\frac{3}{2}}} ( 2 \pi a - 0 )$ $= \dfrac{aI}{4 \pi \left( a^2 + y^2 \right)^{\frac{3}{2}}} \cdot 2 \pi a$ $= \dfrac{a^2 I}{2 \left( a^2 + y^2 \right)^{\frac{3}{2}}}$
$\therefore H = \dfrac{a^2 I}{2 \left( a^2 + y^2 \right)^{\frac{3}{2}}}$ …⑬ (←これが円形コイルの中心軸上(点 $\mathrm{P}$)の磁界の大きさの式)
したがって、求める円形コイルの中心の磁界の大きさは、⑬式に $y=0$ を代入して、
$H = \dfrac{a^2 I}{2 \left( a^2 + 0^2 \right)^{\frac{3}{2}}} = \dfrac{a^2 I}{2 a^3} = \dfrac{I}{2a}$
$\therefore H = \dfrac{I}{2a}$ [$ \mathrm{A / m} $]
となります。
ビオ・サバールの法則のまとめ
ビオ・サバールの法則についてまとめると次のようになります。
- ビオ・サバールの法則を使うと、電線に流れる電流によって作られる磁界の大きさを求めることができる
- ビオ・サバールの法則の式: $dH = \dfrac{I \, dl \sin \theta}{4 \pi r^2}$
- 無限直線状電流により作られる磁界の大きさ: $H = \dfrac{I}{2 \pi a}$
- 円形コイル電流により作られるコイル中心の磁界の大きさ: $H = \dfrac{I}{2a}$
磁界の向きについて
このページでは磁界の向き(方向)については解説しませんでしたが、磁界の向きは右ねじの法則に従った向きになります。右ねじの法則についてはこちらの右ねじの法則のページにまとめていますので参考にしてみてください。
スポンサーリンク
スポンサーリンク
右ねじの法則 ←BACK
NEXT→ フレミングの左手の法則と右手の法則
スポンサーリンク
ビオ・サバールの法則 関連ページ
- クーロンの法則
- 電気磁気学の「クーロンの法則」について解説しています。クーロンの法則は電気磁気学の中でも特に重要な法則で、電荷間に働く力を求めるときなどに使われます。このページではクーロンの法則をできるだけ簡単に理解できるように、電荷のイメージから解説しています。
- 右ねじの法則
- 電気磁気学の「右ねじの法則」とその使い方についてできるだけ簡単に解説しています。右ねじの法則は電流と磁界の向き(方向)の関係を表わした法則で、アンペールの右ねじの法則とか、アンペアの右ねじの法則と呼ばれたりもします。
- フレミングの左手の法則と右手の法則
- 「フレミングの左手の法則」と「フレミングの右手の法則」について解説しています。フレミングの左手の法則と右手の法則は、「電流の向き」と「磁界の向き」と「力の向き」の関係を表わした法則で、「力の向き」を求めるときはフレミングの左手の法則、「電流の向き」を求めるときはフレミングの右手の法則を使います。
- 電界中の電子の運動
- 電界中の電子の運動について解説しています。電界中に電子を置いたときや、電界に電子が突入したときの電子の運動について解説していますので、電界中の電子の運動の勉強の参考にしてみてください。
- 電界中の電子のエネルギーと電子が陽極に達したときの速度
- 電界中の電子のエネルギーと電子が陽極に達したときの速度について解説しています。電界中の電子の位置エネルギーや運動エネルギーなどについて解説していますので、電界中の電子のエネルギーの勉強の参考にしてみてください。
- ローレンツ力
- ローレンツ力について解説しています。ローレンツ力の力の向きや大きさの求め方、円運動などについても解説していますので、ローレンツ力の勉強の参考にしてみてください。
- 電磁誘導
- 電気磁気学の「電磁誘導」と「電磁誘導に関するファラデーの法則」について解説しています。電磁誘導は、コイルを貫く磁束が変化するとコイルに起電力(誘導起電力)が発生する現象です。
- レンツの法則
- 電気磁気学の「レンツの法則」について解説しています。電磁誘導により発生する誘導起電力は、コイルを貫く磁束の変化を妨げるような向きに生じます。これをレンツの法則といいます。


