スポンサーリンク
図形の面積を求める公式
※ページ内にPR・広告が含まれる場合があります。
図形の面積を求める公式は、ふだんあまり使っていないと、
あれ? どんな公式だったかなぁ?
と、忘れてしまったりします。
このページでは、三角形や円などの平面図形の面積を求める公式についてまとめていますので、
この図形の面積はどうやって求めるの?とか、
面積を求める公式を忘れてしまった!
なんてときに、参考にしてみてください。
スポンサーリンク
三角形の面積を求める公式
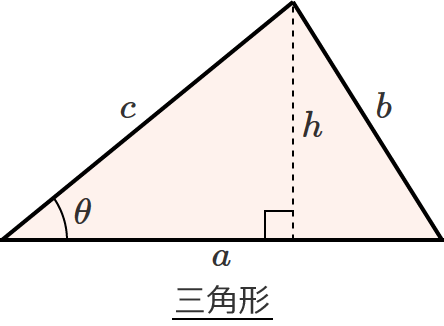
● 面積 $S=\dfrac{1}{2} a\, h$ …①
小学校のときに、「底辺×高さ÷2」と習った公式です。
三角形の面積を求める公式には、sin(サイン)を使った次のような公式もあります。
● 面積 $S=\dfrac{1}{2} a\, c\sin\theta$ …②
$h=c\sin\theta$ なので、これを①式に代入すると②式になります。
また、三角形の3つの辺の長さ($a$、$b$、$c$)から面積を求めることができる次のような公式もあります。(ヘロンの公式といいます。)
$s=\dfrac{a+b+c}{2}$ とすると、
● 面積 $S=\sqrt{s\left( s-a\right)\left( s-b\right)\left( s-c\right)}$
三角形の面積を求める公式は色々あるのね。
正方形(正四角形)の面積を求める公式
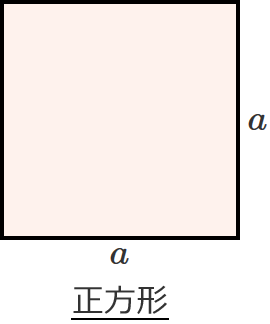
● 面積 $S=a\times a=a^2$
長方形の面積を求める公式
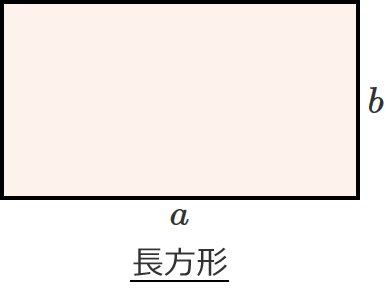
● 面積 $S=a\, b$
平行四辺形の面積を求める公式
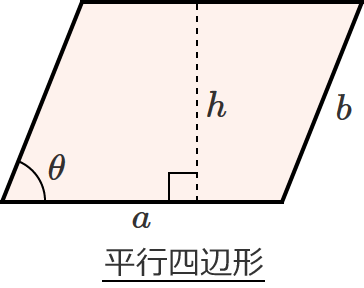
● 面積 $S=a\, h$ …③
平行四辺形の面積を求める公式には、$\sin$(サイン)を使った次のような公式もあります。
● 面積 $S=a\, b\sin\theta$ …④
$h=b\sin\theta$ なので、これを③式に代入すると④式になります。
台形の面積を求める公式
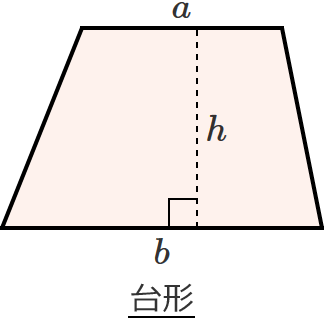
● 面積 $S=\dfrac{1}{2} \left( a+b\right) h$
小学校のときに、「(上底+下底)× 高さ ÷ 2」と習った公式です。
ひし形の面積を求める公式
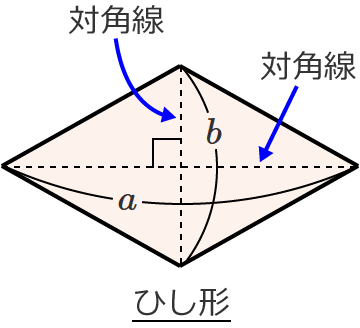
● 面積 $S=\dfrac{1}{2} a\, b$
ひし形の2つの対角線の長さをかけて2で割ると、ひし形の面積になります。
正六角形の面積を求める公式
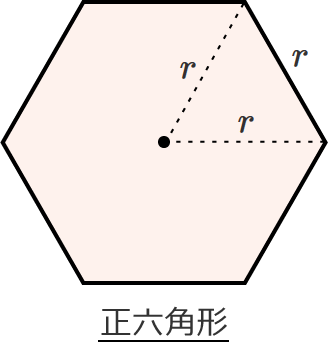
● 面積 $S=\dfrac{3\sqrt{3}}{2} r^2$ …⑤
上の図の $r$ で囲まれた正三角形の面積を求めて、それを6倍すると⑤式になります。
円の面積を求める公式
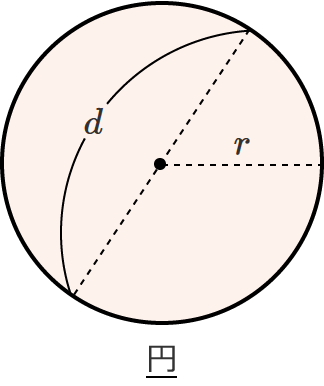
● 面積 $S=\pi\, r^2$ …⑥
円の面積を求める公式は、半径 $r$ ではなく直径 $d$ で表わすと次のような公式になります。
● 面積 $S=\dfrac{\pi\, d^2}{4}$ …⑦
半径 $=\dfrac{\text{直径}}{2}$ なので、$r=\dfrac{d}{2}$ を⑥式に代入すると⑦式になります。
ちなみに、円の円周を求める公式は、
● 円周 $L=2\pi\, r$ (半径 $r$ で表わした場合)
● 円周 $L=\pi\, d$ (直径 $d$ で表わした場合)
です。
扇形の面積を求める公式
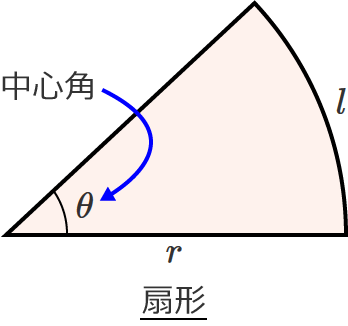
● 面積 $S=\pi\, r^2\dfrac{\theta}{360}$ (中心角 $\theta$ の単位が ${}^\circ$(度)の場合)
● 面積 $S=\dfrac{1}{2} r^2\theta$ (中心角 $\theta$ の単位が $\mathrm{rad}$(ラジアン)の場合)
扇形の面積を求める公式には、半径 $r$ と弧の長さ $l$ だけで表わした次のような公式もあります。
● 面積 $S=\dfrac{1}{2} r\, l$
ちなみに、弧の長さを求める公式は、
● 弧の長さ $l=2\pi\, r\dfrac{\theta}{360}$ (中心角 $\theta$ の単位が ${}^\circ$(度)の場合)
● 弧の長さ $l=r\,\theta$ (中心角 $\theta$ の単位が $\mathrm{rad}$(ラジアン)の場合)
楕円の面積を求める公式
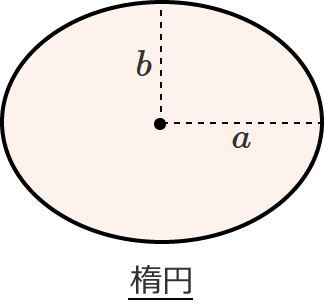
● 面積 $S=\pi\, a\, b$
図形の面積を求める公式の一覧表
以上の図形の面積を求める公式を一覧表にまとめると、次の表のようになります。
| 図形 | 面積を求める公式 |
|---|---|
| 三角形 | $S=\dfrac{1}{2}a\, h$ |
| $S=\dfrac{1}{2}a\, c\sin\theta$ | |
| $S=\sqrt{s\left( s-a\right)\left( s-b\right)\left( s-c\right)}$ $\left(\text{ただし、} s=\dfrac{a+b+c}{2}\right)$ | |
| 正方形 | $S=a^2$ |
| 長方形 | $S=a\, b$ |
| 平行四辺形 | $S=a\, h$ |
| $S=a\, b\sin\theta$ | |
| 台形 | $S=\dfrac{1}{2}\left( a+b\right) h$ |
| ひし形 | $S=\dfrac{1}{2}a\, b$ ($a$、$b$ は対角線の長さ) |
| 正六角形 | $S=\dfrac{3\sqrt{3}}{2}r^2$ |
| 円 | $S=\pi\, r^2$ ($r$ は半径) |
| $S=\dfrac{\pi\, d^2}{4}$ ($d$ は直径) | |
| 扇形 | $S=\pi\, r^2\dfrac{\theta}{360}$ ($\theta$ の単位が ${^\circ}$(度)の場合) |
| $S=\dfrac{1}{2} r^2\theta$ ($\theta$ の単位が $\mathrm{rad}$(ラジアン)の場合) | |
| $S=\dfrac{1}{2}r\, l$ | |
| 楕円 | $S=\pi\, a\, b$ |
ふだんからよく使う公式はあまり忘れることはありませんが、たまにしか使わないような公式は忘れやすいです。(例えば、扇形とか楕円の面積の公式とかね。)
公式をただ丸暗記してもかまわないのですが、公式がなぜそのような形の式になるのか?を考えながらおぼえるようにすると忘れにくくなります。
スポンサーリンク
スポンサーリンク
立体の体積を求める公式については、こちらの立体の体積を求める公式のページを参考にしてみてください。
電気数学のお勉強 ←BACK
NEXT→ 立体の体積を求める公式
スポンサーリンク
図形の面積を求める公式 関連ページ
- 立体の体積を求める公式
- 直方体、三角柱、円柱、三角錐、円錐、球、中空球、楕円体などの立体の体積を求めるときに使う公式についてまとめています。立体の体積を求めたいときや、体積の公式を忘れてしまったときなどの参考にしてみてください。
- 三平方の定理(ピタゴラスの定理)
- 三平方の定理(ピタゴラスの定理)について解説しています。三平方の定理の式(公式)、使い方、証明などについて解説していますので、三平方の定理の勉強の参考にしてみてください。
- 正方形の対角線の長さの求め方
- 正方形の対角線の長さの求め方について解説しています。正方形の対角線の長さを求めるときの参考にしてみてください。
- 長方形の対角線の長さの求め方
- 長方形の対角線の長さの求め方について解説しています。長方形の対角線の長さを求めるときの参考にしてみてください。
- 平行四辺形の対角線の長さの求め方
- 平行四辺形の対角線の長さの求め方について解説しています。平行四辺形の「辺の長さ」と「高さ」が分かっている場合、平行四辺形の「辺の長さ」と「角度」が分かっている場合について解説していますので、平行四辺形の対角線の長さを求めるときの参考にしてみてください。
- ひし形の対角線の長さの求め方
- ひし形の対角線の長さの求め方について解説しています。「対角線の半分の長さを求めてそれを2倍して求める方法」、「対角線を斜辺とする直角三角形を書いて三平方の定理を使って求める方法」について解説していますので、ひし形の対角線の長さを求めるときの参考にしてみてください。
- 立方体の対角線の長さの求め方
- 立方体の対角線の長さの求め方について解説しています。立方体の対角線の長さを求めるときの参考にしてみてください。
- 直方体の対角線の長さの求め方
- 直方体の対角線の長さの求め方について解説しています。直方体の対角線の長さを求めるときの参考にしてみてください。

